【离散数学期复习系列】六、树-Toy模板网

这篇具有很好参考价值的文章主要介绍了【离散数学期复习系列】六、树。希望对大家有所帮助。如果存在错误或未考虑完全的地方，请大家不吝赐教，您也可以点击"举报违法"按钮提交疑问。

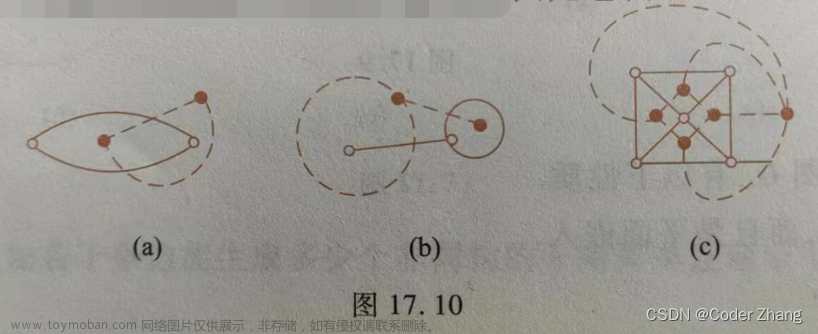
1.什么是树？
无向树(树):不含回路的连通无向图
森林:每个连通分支均是树的非连通无向图
平凡树:平凡图
树叶:树中度数为1的顶点
分支点:树中度数大于等于2的顶点，也就是根节点和内点

2.树的相关性质
设G=<V,E>,|V|=n,|E|=m,则下面各命题是等价的:
(1)G连通且不含回路;
(2)G的每对顶点之间有唯一的一条路径; ‘
(3)G是连通的且m=n-1;
(4)G中无回路且m=n-1;
(5)G中无回路,但在任两个不相邻的顶点之间增加一条边,就形成唯一的一条初级回路;
(6)G是连通的且每条边都是桥.

3.树的相关定理
n阶非平凡的树中至少有2片树叶
证明:非平凡树,每个顶点度数都大于等于1,
设有k片树叶,m=n-1
根据握手定理2m>=k*1+(n-k)*2k>=2
4.生成树
(1)生成树:设G=<V,E>是无向连通图,T是G的生成子图并且是树,则称T是G的生成树
G在T中的边称为T的树枝,不在T中的边称为T的弦.
T的所有弦的集合的导出子图称为T的余树（余树不一定是树,也不一定连通）
(2)设n阶连通无向图有m条边，则它的生成树有n一1条边，余树有m-n十1条边.

5.生成树的性质
(1)任何无向连通图都有生成树，只要是连通图就有树
(2)推论:设n阶无向连通图G有m条边,则m>=n-1.（未破圈之前）

6.弦的回路
基本回路:设T是连通图G=<V,E>的一棵生成树,对每一条弦e,存在唯一的由弦e和T的树枝构成的初级回路Ce, 称Ce为对应于弦e的基本回路.
基本回路系统:所有基本回路的集合为对应生成树T的基本回路系统基本回路的个数都等于m-n+1（就是余数的边数）

7.最小生成树
(1)设T是无向连通带权图G=<V,E,W>的生成树，T中所有边的权之和称为T的权,记作W(T).
(2)最小生成树: 带权图权最小的生成树
(3)最小生成树问题是：求任给的无向连通带权图的最小生成树:
求最小生成树的算法：
破圈法：去掉无向连通图中每个回路中的权值最大的边
避圈法 (Kruskal 库斯克算法) —求最小生成树的算法
1)将每条边按权值大小从小到大排列
2)按从小到大依次选取,若形成环则舍去当前选择的边,直到选n-1条边

8.有向树
有向树: 基图为无向树的有向图
根树: 有一个顶点入度为0, 其余的入度均为1的
非平凡的有向树
树根: 有向树中入度为0的顶点
树叶: 有向树中入度为1, 出度为0的顶点
内点: 有向树中入度为1, 出度大于0的顶点
分支点: 出度大于1的点，树根与内点的总称
顶点v的层数: 从树根到v的通路长度（树根为0层）
树高: 有向树中顶点的最大层数

9.家族树:
(1) 若顶点 a 邻接到顶点 b, 则称 b 是 a 的儿子, a是b 的父亲;
(2) 若b和c为同一个顶点的儿子, 则称b和c是兄弟;
(3) 若a≠b且a可达b, 则称a是b的祖先, b是a的后代.
(4)父亲也可以是儿子的祖先

10.根子树:设v为根树的一个顶点且不是树根, 称v及其所有后代的导出子图为以v为根的根子树.

11.有序树: 将根树同层上的顶点规定次序
r叉树:根树的每个分支点至多有r个儿子
r叉正则树: 根树的每个分支点恰有r个儿子
r叉完全正则树: 树叶层数相同的r叉正则树
r叉有序树: 有序的r叉树
r叉正则有序树: 有序的r叉正则树
r叉完全正则有序树: 有序的r叉完全正则树

12.最优二叉树
设2叉树T有t片树叶v1, v2, …, vt, 树叶的权分别为w1, w2, …, wt, 称为T的权, 其中
l(vi)是vi的层数. 在所有权为w1, w2, …, wt 的t片树叶的2叉树中, 权最小的2叉树称为最优2叉树.

【离散数学期复习系列】六、树

最优二叉树的总权=为各顶点的权值与层数乘积之和
求最优2叉树的算法
Huffman（哈夫曼）算法:
给定实数w1, w2, …, wt ,
① 作t片树叶, 分别以w1, w2, …, wt为权.
② 在所有入度为0的顶点(不一定是树叶)中选出两个权最小的顶点, 添加一个新分支点, 以这2个顶点为儿子, 其权等于这2个儿子的权之和.
③ 重复②, 直到只有1个入度为0 的顶点为止.
W(T)等于：
1.所有分支点的权之和
或 2.树叶权值乘以层数之和

13.设a =α1α2…αn-1αn是长度为n的符号串
α的前缀: α1α2…αk , k=1,2,…,n-1,n
前缀码: {β1, β2, …, βm}, 其中β1, β2, …, βm为非空字符串, 且任何两个互不为前缀
2元前缀码: 只有两个符号(如0与1)的前缀码xβα
{0,10,110, 1111}, {10,01,001,110}是2元前缀码 {0,10,010, 1010} 不是前缀码
一棵2叉树产生一个二元前缀码:
对每个分支点, 若关联2条边, 则给左边标0, 右边标1;若只关联1条边, 则可以给它标0(看作左边), 也可以标1(看作右边). 将从树根到每一片树叶的通路上标的数字组成的字符串记在树叶处, 所得的字符串构成一个前缀码.
【离散数学期复习系列】六、树