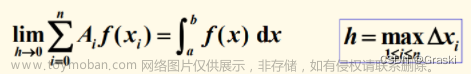文章来源地址https://www.toymoban.com/news/detail-427472.html
书上例题：
例3
确定求积公式
中的系数，使其具有尽可能高的代数精度。
我的答案：
一、信息
1.给了我一个求积公式
2.确定求积公式中的系数
3.使得这个求积系数具有尽可能高的代数精度。
二、分析
条件1：告诉我这个求积公式具体有3个未知量
条件2：告诉我此次问题解答的目标1是确定系数A-1，A0，A1
条件3：告诉我第二个目标是使得求积系数具有尽可能高的代数精度
三、思考
疑问：如何确定系数呢？
解答
1.思路：确定方程中的未知量(即系数)就要列等式，有n个未知量就要列n个等式
疑问：如何构造等式呢？
2.这个题目已经告诉我是有关代数精度的了构造等式有可能可以从代数精度的知识点入手：
通过回忆我发现
关于这个知识点的内容在5.2 构造数值积分公式的基本方法与有关概念(不熟悉的同学可以传送到这一篇文章中学习)中的5.2.3 数值积分公式的代数精度中，而这一小节的公式只有一个那就是
定义1
不难看出此处的f(x)是任意的，又由于这个题目又三个未知量，因此我们不妨设三个函数f(x)=1,x,x^(2)，那么我们就可以构建其三个等式带入公式，得到答案
目标2 使其具有尽可能高的代数精度
疑问：如何才能达到这个目标呢？
解答：
由于求积公式所有系数已经确定，我们可以继续根据定义1来判断它，定义1已经清楚的说明了代数精度的定义，因此我们继续给f(x)升幂，随着幂数的上升我们不难发现当m=4时，不满足左端=右端因此，该求积公式的代数精度为3
四、解答
例4 （注意未知量个数）求积公式的应用2
我的答案：
和例3的信息一样
我们来直接进入到分析过程
二、分析
1.有几个未知量，四个注意此处参数也是未知量
2.接下来的大差不差了
四、解答：
文章来源：https://www.toymoban.com/news/detail-427472.html
到了这里，关于5.2 构造数值积分公式的基本方法与有关概念的例题分析的文章就介绍完了。如果您还想了解更多内容，请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章，希望大家以后多多支持TOY模板网！
