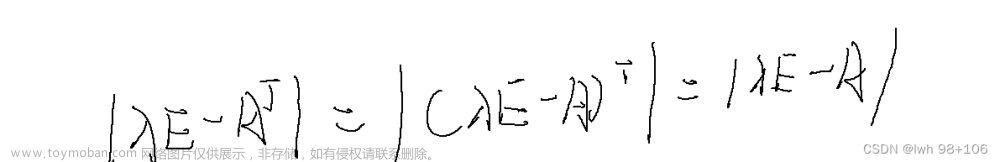线性代数中的特征值和特征向量

7月前作者：驼驼学编程分类：Toy博客阅读(32) 违法举报

这篇具有很好参考价值的文章主要介绍了线性代数中的特征值和特征向量。希望对大家有所帮助。如果存在错误或未考虑完全的地方，请大家不吝赐教，您也可以点击"举报违法"按钮提交疑问。

一.几个基本概念

现将下文需要运用到的一些概念进行解释说明以便读者更好理解

1.特征值与特征向量

线性代数中的特征值和特征向量

其中，我们要注意两点：

（1）A是方阵（对于非方阵，是没有特征值的，但会有条件数）

（2）特征向量为非0列向量

我们再来看看两个相关定理

线性代数中的特征值和特征向量

定理5.1说明了一个矩阵的几个特征向量线性无关

定义5.1的第一个式子说明了矩阵特征向量的和等于对应方阵行列式对角线元素的和，第二个式子说明了矩阵特征向量的乘积等于对于方阵行列式的值

还有一些对运算有帮助的公式

（1）(A+kE)a=(λ+k)a

（2）A²a=A(λa)=λAa=λ²a

2.矩阵可逆的条件

1 .秩等于行数
2 .行列式不为0，即|A|≠0
3 .行向量(或列向量)是线性无关组
4 .存在一个矩阵,与它的乘积是单位阵
5 .齐次线性方程组AX=0 仅有零解
6 .非齐次线性方程组AX=b 有唯一解
7 .可以经过初等行变换化为单位矩阵，即该矩阵等价于n阶单位矩阵
8 .它去左(右)乘另一个矩阵,秩不变

注意：可逆矩阵的特征值不等于0

3.相似矩阵的概念与性质

线性代数中的特征值和特征向量

4.矩阵相似的必要条件

（1）特征多项式相同，即|λE-A|=|λE-B|

（2）A，B有相同的特征值

（3）r（A）=r（B）

（4）|A|=|B|=特征值的乘积

（5）矩阵对角线之和相同，等于特征值的和

5.矩阵相似的两个定理

线性代数中的特征值和特征向量

6.实对称矩阵三大定理

线性代数中的特征值和特征向量

二.一张表格

矩阵	特征值
A	λ
A^T（A的转置）	λ
KA	Kλ
A^m（m为常数）	λ^m
A^-1（逆矩阵）	λ^-1
A*（A的伴随）	\|A\|/λ
~（相似矩阵）	λ

三.三个解题步骤

1.特征向量与特征值

（1）步骤

（1）利用|λE-A|=0求出λ

（2）将λ带入|λE-A|=0求出特征向量

（2）例题

线性代数中的特征值和特征向量

2.相似矩阵

（1）步骤

线性代数中的特征值和特征向量

（2）例题

线性代数中的特征值和特征向量

线性代数中的特征值和特征向量

3.实对称矩阵

（1）步骤

线性代数中的特征值和特征向量

（2）例题

线性代数中的特征值和特征向量

线性代数中的特征值和特征向量

文章来源地址https://www.toymoban.com/news/detail-427487.html

到了这里，关于线性代数中的特征值和特征向量的文章就介绍完了。如果您还想了解更多内容，请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章，希望大家以后多多支持TOY模板网！

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：如若内容造成侵权/违法违规/事实不符，请点击违法举报进行投诉反馈，一经查实，立即删除！

分享到：

领支付宝红包赞助服务器费用

线性代数基础【5】特征值和特征向量

一、特征值和特征向量的理论背景在一个多项式中,未知数的个数为任意多个,且每一项次数都是2的多项式称为二次型,二次型分为两种类型:即非标准二次型及标准二次型注意: ①二次型X^T AX为非标准二次型的充分必要条件是A^T=A 但A为非对角矩阵;二次型 X^TAX为标准二次型的充

2024年01月20日
浏览(34)
线性代数学习之特征值与特征向量

在上一次线性代数学习之行列式学习了行列式相关的一些概念，其中也多次提到学好行列式是为了学习“特征值和特征向量”的基础，所以此次就正式进入这块内容的学习，也是线性代数中非常重要的概念，因为它又是线性代数其它重要概念的基石比如矩阵的相似性等等，当

2024年02月11日
浏览(38)
线性代数第五章特征值与特征向量

一、特征值定义二、特征值求法定义法；；相似。三、特征向量求法定义法；基础解系法；；相似。四、特征值性质不同特征值的特征向量线性无关 k重特征值至多有k个线性无关的特征向量五、相似的定义若，则A和B相似。六、相似的性质（必要条件）七、可对角

2024年02月06日
浏览(35)
线性代数——特征值与特征向量的性质

（1）设A为方阵，则A与 A T A^{T} A T 有相同的特征值。此处用到了两个关键性质，一：单位阵的转置为其本身,二：转置并不改变行列式的值。（2）：设n阶方阵A=（ a i j a_{ij} a ij ）的n个特征值为 λ 1 lambda_{1} λ 1 , λ 2 lambda_{2} λ 2 ,… λ n lambda_{n} λ n ,则 λ 1 + λ

2024年02月04日
浏览(29)
线性代数（8）：特征值、特征向量和相似矩阵

有矩阵 A 为 n 阶矩阵，Ax = λx （ λ 为一个实数，x为 n 维非零列向量），则称 λ 为方阵 A 的特征值， x 为特征向量； 1.2.1 公式求特征值：使 | A - λE | = 0，其解的 λ 值即为矩阵 A 的特征值；求特征向量：使 ( A - λE )x = 0,设 x 为与 A 具有

2024年02月11日
浏览(34)
数值线性代数：Arnoldi求解特征值/特征向量

线性方程组求解、最小二乘法、特征值/特征向量求解是(数值)线性代数的主要研究内容。在力学、气象学、电磁学、金融等学科中，许多问题最终都归结为特征值、特征向量的求解。 ARPACK 使用 IRAM ( Implicit Restarted Arnoldi Method )求解大规模系数矩阵的部分特征值与特征向量

2024年01月18日
浏览(43)
线性代数---第五章特征值和特征向量

当特征值是二重根时，有可能有一个线性无关的特征向量，也有可能有两个线性无关的特征向量

2023年04月17日
浏览(27)
线性代数中矩阵的特征值与特征向量

作者：禅与计算机程序设计艺术在线性代数中，如果一个$ntimes n$的方阵$A$满足如下两个条件之一： $A$存在实数特征值，即$exists xneq 0:Ax=kx$,其中$kin mathbb{R}$； $lambda_{max}(A)neq 0$（$lambda_{max}(A)$表示$A$的最大特征值），且$||x_{lambda_{max}(A)}||=sqrt{frac{lambda_{max}(A)}{lambda_{

2024年02月08日
浏览(33)
线性代数（五） | 矩阵对角化特征值特征向量

矩阵实际上是一种变换,是一种旋转伸缩变换（方阵）不是方阵的话还有可能是一种升维和降维的变换直观理解可以看系列超赞视频线性代数-哔哩哔哩_Bilibili 比如A= ( 1 2 2 1 ) begin{pmatrix}12\\\\21end{pmatrix} ( 1 2 2 1 ) x= ( 1 2 ) begin{pmatrix}1\\\\2end{pmatrix} ( 1 2 ) 我们给x左乘A实际

2024年02月04日
浏览(42)
线性代数｜证明：矩阵不同特征值对应的特征向量线性无关

定理 1 设 λ 1 , λ 2 , ⋯ , λ m lambda_1,lambda_2,cdots,lambda_m λ 1 , λ 2 , ⋯ , λ m 是方阵 A boldsymbol{A} A 的 m m m 个特征值， p 1 , p 2 , ⋯ , p m boldsymbol{p}_1,boldsymbol{p}_2,cdots,boldsymbol{p}_m p 1 , p 2 , ⋯ , p m 依次是与之对应的特征向量，如果 λ 1 , λ 2 , ⋯ , λ

2024年02月07日
浏览(37)