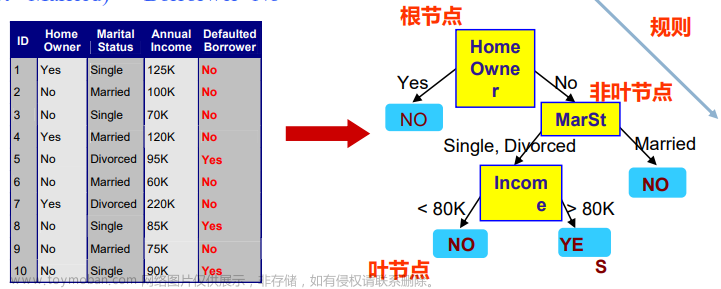
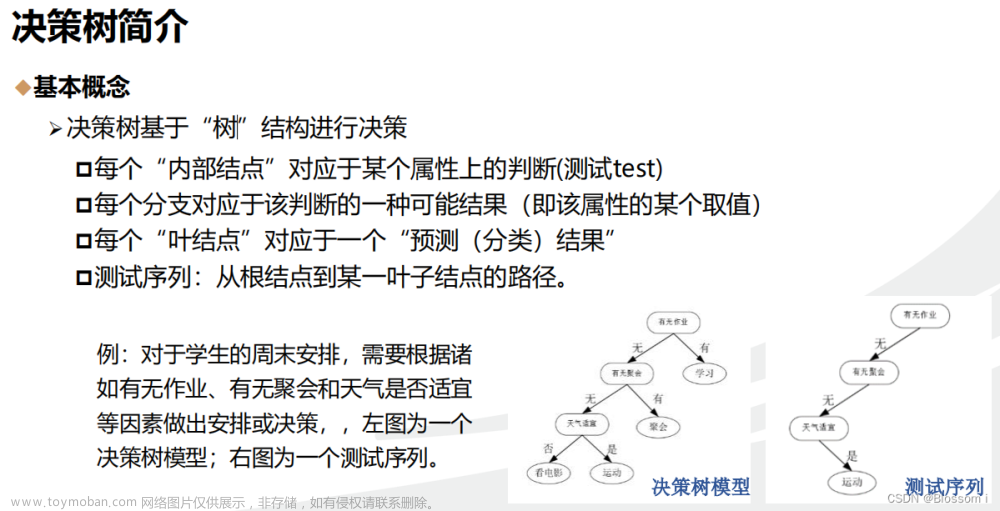
决策树之用信息增益选择最优特征-Toy模板网

这篇具有很好参考价值的文章主要介绍了决策树之用信息增益选择最优特征。希望对大家有所帮助。如果存在错误或未考虑完全的地方，请大家不吝赐教，您也可以点击"举报违法"按钮提交疑问。

决策树之用信息增益选择最优特征

熵

熵的定义: 熵（shāng），热力学中表征物质状态的参量之一，用符号S表示，其物理意义是体系混乱程度的度量。

在决策树中，信息增益是由熵构建而成，表示的是[随机变量的不确定性]，不确定性越大，代表着熵越大。随机变量的取值等概率分布时，相应的熵最大，换句话说，特征的所有取值概率相同时，包含的信息是最多的，就是不确定性最大的情况。

熵和随机变量的分布相关，所以写成：
$H(p)=-\sum_{i=1}^{n} p_{i} \log p_{i}\\$
随机变量取值等概率分布时，相应的熵最大,熵的取值范围为:
$\leq H(p) \leq \log n$
例如：
$\begin{cases}0, & \text {概率}=p \\ 1, & \text { 概率= }1-p\end{cases}$
熵就是：
$H(p)=-\sum_{i=1}^{n} p_{i} \log p_{i}\\=-p \log _{2} p-(1-p) \log _{2}(1-p)$
对p求导：
$\begin{aligned} \frac{\partial H(p)}{\partial p} &=-\log _{2} p-\frac{1}{\ln 2}+\log _{2}(1-p)+\frac{1}{\ln 2} \\ &=\log _{2} \frac{1-p}{p} \end{aligned}$
找到熵的极值点：
$\log _{2} \frac{1-p}{p}=0\\ \frac{1-p}{p}=1\\ p=\frac{1}{2}$
即当 $p=\frac{1}{2}$ 时，熵取最大值

信息增益

信息增益：得知特征X而使类Y的信息的不确定性减少的程度。
 公式为： g(D,A)=H(D)-H(D A)

当熵和条件熵中的概率有数据估计得到时，则为经验熵和经验条件嫡。

计算信息增益步骤：

输入：训练数据集D和特征A
 输出：特征A对D的信息增益g(D,A)

计算经验熵公式：
$H(D)=-\sum_{k=1}^{K} \frac{\left|C_{k}\right|}{|D|} \log _{2} \frac{\left|C_{k}\right|}{|D|}$
计算经验条件熵公式
$\mid A)=\sum_{i=1}^{n} \frac{\left|D_{i}\right|}{|D|} H\left(D_{i}\right)=-\sum_{i=1}^{n} \frac{\left|D_{i}\right|}{|D|} \sum_{k=1}^{K} \frac{\left|D_{i k}\right|}{\left|D_{i}\right|} \log _{2} \frac{\left|D_{i k}\right|}{\left|D_{i}\right|}$

$H\left(D \mid A_{1}\right)=w_{1} H\left(D_{1}\right)+w_{2} H\left(D_{2}\right)+w_{3} H\left(D_{3}\right)$

这里的嫡和条件熵中的概率由数据估计得到的，为经验熵和经验条件熵。在特征A 下每个子集所占的权重为 $w_{i}=\frac{\left|D_{i}\right|}{|D|}$
计算信息增益公式:
$g (D, A) = H (D) - H (D A)$

信息增益例题：

决策树之用信息增益选择最优特征

计算经验熵公式
1. 样本15个，按是否贷款分为两类，同意贷款个数=9，不同意贷款个数=6
  
  代入计算：
  $\begin{aligned} H(D) &=-\sum_{k=1}^{K} \frac{\left|C_{k}\right|}{|D|} \log _{2} \frac{\left|C_{k}\right|}{|D|} \\ &=-\frac{6}{15} \log _{2} \frac{6}{15}-\frac{9}{15} \log _{2} \frac{9}{15} \\ &=0.971 \end{aligned}$
计算经验条件熵公式
1. $A_1、A_2、A_3、A_4$ 表示年龄、工作、房子、信贷情况4个特征
特征：年龄 $A_1$ :取 $i$ =1青年、 $i$ =2中年、 $i$ =3老年

青年：
$\begin{aligned} &w_{1}=\frac{\left|D_{1}\right|}{|D|}=\frac{5}{15} \\ &H\left(D_{1}\right)=-\sum_{k=1}^{2} \frac{\left|D_{1 k}\right|}{\left|D_{1}\right|} \log _{2} \frac{\left|D_{1 k}\right|}{\left|D_{1}\right|}=-\frac{3}{5} \log _{2} \frac{3}{5}-\frac{2}{5} \log _{2} \frac{2}{5}=0.972 \end{aligned}$
中年：
$\begin{aligned} &w_{2}=\frac{\left|D_{2}\right|}{|D|}=\frac{5}{15} \\ &H\left(D_{2}\right)=-\sum_{k=1}^{2} \frac{\left|D_{2 k}\right|}{\left|D_{2}\right|} \log _{2} \frac{\left|D_{2 k}\right|}{\left|D_{2}\right|}=-\frac{2}{5} \log _{2} \frac{2}{5}-\frac{3}{5} \log _{2} \frac{3}{5}=0.972 \end{aligned}$
老年：
$\begin{aligned} &w_{3}=\frac{\left|D_{3}\right|}{|D|}=\frac{5}{15} \\ &H\left(D_{3}\right)=-\sum_{k=1}^{2} \frac{\left|D_{3 k}\right|}{\left|D_{3}\right|} \log _{2} \frac{\left|D_{3 k}\right|}{\left|D_{3}\right|}=-\frac{1}{5} \log _{2} \frac{1}{5}-\frac{4}{5} \log _{2} \frac{4}{5}=0.720 \end{aligned}$
综合计算经验条件熵 $H\left(D \mid A_{1}\right)$ :
$\begin{aligned} H\left(D \mid A_{1}\right) &=w_{1} H\left(D_{1}\right)+w_{2} H\left(D_{2}\right)+w_{3} H\left(D_{3}\right) \\ &=0.324+0.324+0.24 \\ &=0.888 \end{aligned}$
计算信息增益公式
$\begin{aligned} g\left(D, A_{1}\right) &=H(D)-H\left(D \mid A_{1}\right) \\ &=0.971-0.888=0.083 \end{aligned}$
同理

特征：房子

决策树之用信息增益选择最优特征
有工作：
$\begin{aligned} &w_{1}=\frac{\left|D_{1}\right|}{|D|}=\frac{5}{15} \\ &H\left(D_{1}\right)=-\sum_{k=1}^{2} \frac{\left|D_{1 k}\right|}{\left|D_{1}\right|} \log _{2} \frac{\left|D_{1 k}\right|}{\left|D_{1}\right|}=-\frac{0}{5} \log _{2} \frac{0}{5}-\frac{5}{5} \log _{2} \frac{5}{5}=0 \end{aligned}$
没有工作：
$\begin{aligned} &w_{2}=\frac{\left|D_{2}\right|}{|D|}=\frac{10}{15} \\ &H\left(D_{2}\right)=-\sum_{k=1}^{2} \frac{\left|D_{2 k}\right|}{\left|D_{2}\right|} \log _{2} \frac{\left|D_{2 k}\right|}{\left|D_{2}\right|}=-\frac{6}{10} \log _{2} \frac{6}{10}-\frac{4}{10} \log _{2} \frac{4}{10} \end{aligned}$
综合计算经验条件熵 $H\left(D \mid A_{2}\right)$ :
$\begin{aligned} H\left(D \mid A_{2}\right) &=w_{1} H\left(D_{1}\right)+w_{2} H\left(D_{2}\right)) =0.647 \end{aligned}$
计算信息增益公式
$\begin{aligned} g\left(D, A_{2}\right) &=H(D)-H\left(D \mid A_{1}\right) \\ &=0.971-0.647=0.324 \end{aligned}$
特征：房子

决策树之用信息增益选择最优特征
有房子：
$\begin{aligned} &w_{1}=\frac{\left|D_{1}\right|}{|D|}=\frac{6}{15} \\ &H\left(D_{1}\right)=-\sum_{k=1}^{2} \frac{\left|D_{1 k}\right|}{\left|D_{1}\right|} \log _{2} \frac{\left|D_{1 k}\right|}{\left|D_{1}\right|}=-\frac{0}{6} \log _{2} \frac{0}{6}-\frac{6}{6} \log _{2} \frac{6}{6}=0 \end{aligned}$
没有房子：
$\begin{aligned} &w_{2}=\frac{\left|D_{2}\right|}{|D|}=\frac{9}{15} \\ &H\left(D_{2}\right)=-\sum_{k=1}^{2} \frac{\left|D_{2 k}\right|}{\left|D_{2}\right|} \log _{2} \frac{\left|D_{2 k}\right|}{\left|D_{2}\right|}=-\frac{3}{9} \log _{2} \frac{3}{9}-\frac{6}{9} \log _{2} \frac{6}{9} \end{aligned}$
综合计算经验条件熵 $H\left(D \mid A_{3}\right)$ :
$\begin{aligned} H\left(D \mid A_{3}\right) &=w_{1} H\left(D_{1}\right)+w_{2} H\left(D_{2}\right)) =0.551 \end{aligned}$
计算信息增益公式
$\begin{aligned} g\left(D, A_{3}\right) &=H(D)-H\left(D \mid A_{1}\right) \\ &=0.971-0.551=0.420 \end{aligned}$
特征：信贷情况

决策树之用信息增益选择最优特征

非常好：
$\begin{aligned} &w_{1}=\frac{\left|D_{1}\right|}{|D|}=\frac{4}{15} \\ &H\left(D_{1}\right)=-\sum_{k=1}^{2} \frac{\left|D_{1 k}\right|}{\left|D_{1}\right|} \log _{2} \frac{\left|D_{1 k}\right|}{\left|D_{1}\right|}=-\frac{0}{4} \log _{2} \frac{0}{4}-\frac{4}{4} \log _{2} \frac{4}{4}=0 \end{aligned}$
好：
$\begin{aligned} &w_{2}=\frac{\left|D_{2}\right|}{|D|}=\frac{6}{15} \\ &H\left(D_{2}\right)=-\sum_{k=1}^{2} \frac{\left|D_{2 k}\right|}{\left|D_{2}\right|} \log _{2} \frac{\left|D_{2 k}\right|}{\left|D_{2}\right|}=-\frac{2}{6} \log _{2} \frac{2}{6}-\frac{4}{6} \log _{2} \frac{4}{6} \end{aligned}$
一般：
$\begin{aligned} &w_{3}=\frac{\left|D_{3}\right|}{|D|}=\frac{5}{15} \\ &H\left(D_{3}\right)=-\sum_{k=1}^{2} \frac{\left|D_{3 k}\right|}{\left|D_{3}\right|} \log _{2} \frac{\left|D_{3 k}\right|}{\left|D_{3}\right|}=-\frac{4}{5} \log _{2} \frac{4}{5}-\frac{1}{5} \log _{2} \frac{1}{5} \end{aligned}$
综合计算经验条件熵 $H\left(D \mid A_{4}\right)$ :
$\begin{aligned} H\left(D \mid A_{1}\right) &=w_{1} H\left(D_{1}\right)+w_{2} H\left(D_{2}\right)+w_{3} H\left(D_{3}\right)=0.608 \end{aligned}$
计算信息增益公式
$\begin{aligned} g\left(D, A_{4}\right) &=H(D)-H\left(D \mid A_{4}\right) \\ &=0.971-0.608=0.363 \end{aligned}$
汇总如下：

特征:房子对应的经验熵最小0.551，信息增益 0.420最大，选择这个特征的话，对应的不确定性最小，分类选择最为明确，可以设为最优特征。

注意：不同特征内的分类个数不同，有的是3个，比如年龄（青年、中年、老年），有的是2个，比如工作（有工作、无工作），取值个数较多时，可能计算出的信息增益会更大，从图中可以看出信息增益会更倾向于取值较多的特征。

信息增益更倾向于具有更多选择的那个特征会造成信息增益比更少选择的特征大

例如：信贷情况信息增益0.363大于有工作的信息增益0.324，有可能是因为信贷取值较多而带来的影响。怎么将这个影响降下去，引入信息增益比（在信息增益的情况下，增加一个惩罚项，训练数据集D关于特征A的熵的倒数）。特征A单位取值个数下的信息收益
$特征A单位取值个数下的信息收益g(D,A)/H_A(D)$