目录
一、绘制三维曲线
二、绘制三维曲面
1.meshgrid函数
2.mesh和surf函数
一、绘制三维曲线
1.最基本的绘制三维曲线的函数—plot3
plot3(x1,y1,z1, 选项 1,x2,y2,z2, 选项 2,…, xn,yn,zn , 选项 n)其中,每一组 x , y , z 组成一组曲线的坐标参数,选项的定义和 plot 函数相同。当 x 、 y 、 z 是同维向量时,则 x 、 y 、 z 对应元素构成一条三维曲线;当 x 、 y 、 z 是同维矩阵时,则以 x 、 y 、 z 对应列元素绘制三维曲线,曲线条数等于矩阵列数。(plot详细用法可以参考我的博客:matlab绘图(一)
例1. 绘制三维曲线

代码如下:
t=0:pi/10:10*pi;%取点
x=sin(t)+t.*cos(t);
y=cos(t)-t.*sin(t);
z=t;%计算x,y,z坐标
plot3(x,y,z,'Color','#4F4F2F','Linewidth',1.5);
axis([-30 30 -30 30 0 35])%设置坐标范围
title('Line in 3-D Space');%标题
xlabel('X');ylabel('Y');zlabel('Z');%x,y,z轴标签
grid on;%开启网格线
绘制图形如下:

2.简易绘制三维曲线
对于参数形式表示的三维曲线,还可以用简易绘图函数ezplot3绘制。
调用格式:ezplot3(x,y,z,[a,b])
在区间a < t < b绘制由参数方程x = x (t),y = y (t) 和z = z (t) 确定的三维曲线。未指定区间时,默认在区间0 < t < 2pi绘制图形。
例2. 绘制三维曲线

syms t
x=sin(t)+t.*cos(t);
y=cos(t)-t.*sin(t);
z=t;%计算x,y,z坐标
ezplot3(x,y,z,[0,10*pi])运行结果;

二、绘制三维曲面
1.meshgrid函数
对于函数曲面,即由 z=f( x,y ) , a<x<b, c<y<d 表示的曲面,通常,先在 x 轴的区间 [ a , b ] 内取 n 个点 ,设这些点的 x 坐标构成向量 x; 再在 y 轴的区间 [ c , d ] 内取 m 个点 ,设这些点的 y 坐标构成向量 y; 由各划分点分别作平行于两坐标轴的直线,则得到二维矩形区域 a<x<b, c<y<d 内的 mxn 个网格点 P ij 。这 mxn 个网格点的 x 坐标构成 mxn 的矩阵 X ,它们的 y 坐标构成 mxn 的矩阵 Y ,即第 ( i,j ) 个网格点 P ij 的坐标为 (X( i,j ),Y( i,j )) 。如何由向量 x, y 得到矩阵 X, Y。 Matlab 专门提供了一个函数 meshgrid ,它的功能就是由 x,y 轴的划分点(向量 x,y )生成二维网格点 P ij 的坐标矩阵 X,Y 。
格式 : [X,Y]= meshgrid ( x,y ); 当 y=x 时,可以简化为 [X,Y]= meshgrid (x)。
2.mesh和surf函数
mesh函数用于绘制三维网格图,surf用于绘制三维曲面图,各线条之间的补面用颜色填充。以下介绍mesh的使用格式 (surf与mesh的使用格式相同)。
mesh(X,Y,Z,C) : 其中,X,Y,Z 分别是由曲面上mxn个点的x坐标、y坐标和z坐标构成的mxn的矩阵,即: (X(i,j),Y(i,j),Z(i,j))是第(i,j)个网格点Pij的坐标, C(i,j)是Pij的颜色值。
mesh(X,Y,Z) :使用C=Z(颜色值正比于高度值)
mesh(x,y,Z)或mesh(x,y,Z,C) :使用两个向量代替两个矩阵,要求: length(x)=n, length(y)=m ,且[m,n]=size(Z),第(i,j)个网格点Pij的坐标为(x(j),y(i),Z(i,j))
mesh(Z):等价于mesh(1:n,1:m,Z)。
mesh(Z,C):等价于mesh(1:n,1:m,Z,C)。
例3.绘制函数z=x*exp(-x^2-y^2)在[-2,2]x[-3,3]内的图形。下面两段代码效果是完全一样的。
%% figure1
figure(1)
x=-2:0.1:2; y=-3:0.1:3;
[X,Y]=meshgrid(x,y);
Z=X.*exp(-X.^2-Y.^2);
mesh(X,Y,Z);
title('figure 1')
colorbar%% figure2
figure(2)
x=-2:0.1:2;m=size(x,2);
y=-3:0.1:3; n=size(y,2);
Z=zeros(n,m);
for i=1:m
for j=1:n
Z(j,i)=x(i)*exp(-x(i)^2-y(j)^2);
end
end
mesh(x,y,Z);
colorbar
title('figure 2')
结果展示:


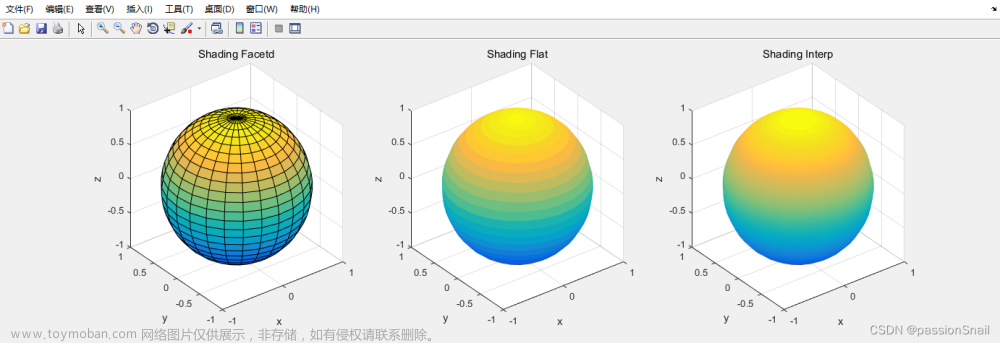
曲面图绘制(只需将mesh改为surf即可),这十张图片体现不同的颜色映射风格,标题为对应的colormap的值。
代码如下:
%% figure 1
figure(1)
x=-2:0.1:2; y=-3:0.1:3;
[X,Y]=meshgrid(x,y);
Z=X.*exp(-X.^2-Y.^2);
surf(X,Y,Z);
title('hsv')
colormap('hsv')
shading flat
%% figure 2
figure(2)
x=-2:0.1:2; y=-3:0.1:3;
[X,Y]=meshgrid(x,y);
Z=X.*exp(-X.^2-Y.^2);
surf(X,Y,Z);
title('jet')
colormap('jet')
shading interp
%% figure 3
figure(3)
x=-2:0.1:2; y=-3:0.1:3;
[X,Y]=meshgrid(x,y);
Z=X.*exp(-X.^2-Y.^2);
surf(X,Y,Z);
title('copper')
colormap('copper')
shading interp
%% figure 4
figure(4)
x=-2:0.1:2; y=-3:0.1:3;
[X,Y]=meshgrid(x,y);
Z=X.*exp(-X.^2-Y.^2);
surf(X,Y,Z);
title('bone')
colormap('bone')
shading interp
%% figure 5
figure(5)
x=-2:0.1:2; y=-3:0.1:3;
[X,Y]=meshgrid(x,y);
Z=X.*exp(-X.^2-Y.^2);
surf(X,Y,Z);
title('flag')
colormap('flag')
shading interp
%% figure 6
figure(6)
x=-2:0.1:2; y=-3:0.1:3;
[X,Y]=meshgrid(x,y);
Z=X.*exp(-X.^2-Y.^2);
surf(X,Y,Z);
title('pink')
colormap('pink')
shading interp
%% figure 7
figure(7)
x=-2:0.1:2; y=-3:0.1:3;
[X,Y]=meshgrid(x,y);
Z=X.*exp(-X.^2-Y.^2);
surf(X,Y,Z);
title('spirng')
colormap('spring')
shading interp
%% figure 8
figure(8)
x=-2:0.1:2; y=-3:0.1:3;
[X,Y]=meshgrid(x,y);
Z=X.*exp(-X.^2-Y.^2);
surf(X,Y,Z);
title('summer')
colormap('summer')
shading interp
%% figure 9
figure(9)
x=-2:0.1:2; y=-3:0.1:3;
[X,Y]=meshgrid(x,y);
Z=X.*exp(-X.^2-Y.^2);
surf(X,Y,Z);
title('autumn')
colormap('autumn')
shading interp
%% figure 10
figure(10)
x=-2:0.1:2; y=-3:0.1:3;
[X,Y]=meshgrid(x,y);
Z=X.*exp(-X.^2-Y.^2);
surf(X,Y,Z);
title('winter')
colormap('winter')
shading interp图像结果展示:










例4.绘制三维曲面图z = sinx^2 + cosy^2,x:[0,pi],y:[0,pi/2]。
代码:
[x,y]=meshgrid(0:pi/100:pi, 0:pi/100:pi/2);
z=sin(x.^2)+cos(y.^2);
surf(x,y,z);
axis([0 4 0 1.8 -1.5 1.5]);
colormap('prism')
shading interp
colorbar运行结果:文章来源:https://www.toymoban.com/news/detail-428016.html
 文章来源地址https://www.toymoban.com/news/detail-428016.html
文章来源地址https://www.toymoban.com/news/detail-428016.html
到了这里,关于matlab绘图(三)绘制三维图像的文章就介绍完了。如果您还想了解更多内容,请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章,希望大家以后多多支持TOY模板网!