SCAU 统计学实验5-Toy模板网

这篇具有很好参考价值的文章主要介绍了SCAU 统计学实验5。希望对大家有所帮助。如果存在错误或未考虑完全的地方，请大家不吝赐教，您也可以点击"举报违法"按钮提交疑问。

SCAU 统计学实验5
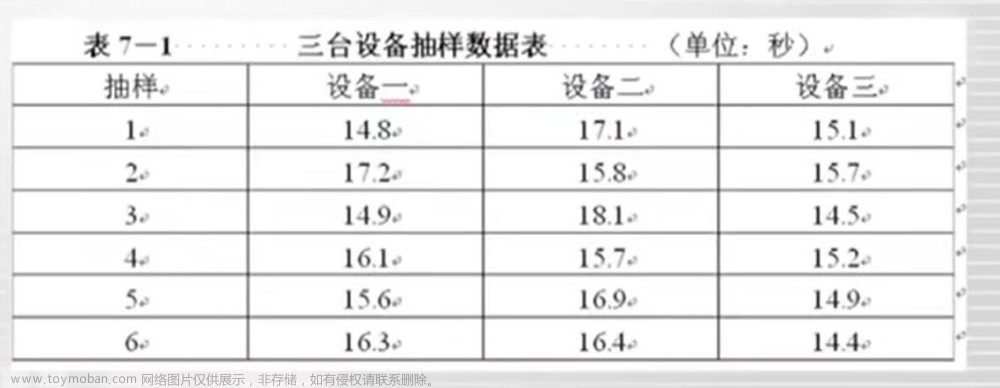
8.14
总体平均值（μ）：7.0 cm
总体方差（σ²）：0.03 cm²
样本平均值（x̄）：6.97 cm
样本方差（s²）：0.0375 cm²
样本大小（n）：80

在这个问题中，我们已经知道总体方差（σ²），所以应该使用 z 检验。

将检验以下零假设（H₀）：
H₀: μ = 7.0 cm

与备择假设（H₁）：
H₁: μ ≠ 7.0 cm

使用双侧检验，因为对螺栓口径偏大或偏小都感兴趣。

先计算 z 统计量：
z = (x̄ - μ) / (σ / √n)

然后，我们将计算双侧检验的 p 值。

如果 p 值小于给定的显著性水平（α = 0.05），我们将拒绝零假设，认为螺栓没有达到规定的要求。

使用 Python 和 SciPy 库来进行计算：

import math
from scipy import stats

# 总体和样本参数
mu = 7.0  # 总体平均值
sigma_squared = 0.03  # 总体方差
x_bar = 6.97  # 样本平均值
sample_size = 80  # 样本量

# 计算标准差和 z 统计量
sigma = math.sqrt(sigma_squared)
z_stat = (x_bar - mu) / (sigma / math.sqrt(sample_size))

# 计算双侧检验的 p 值
p_value = stats.norm.sf(abs(z_stat)) * 2

print("z值为:", z_stat)
print("p值为:", p_value)

alpha = 0.05
if p_value < alpha:
    print("拒绝原假设，螺栓不符合规定要求。")
else:
    print("未能拒绝原假设，螺栓符合规定要求。")

z值为: -1.5491933384829797
p值为: 0.12133525035847904
未能拒绝原假设，螺栓符合规定要求。

8.15
为了解决这个问题，我们可以使用双样本 t 检验，因为我们没有关于总体方差的信息。

将使用以下参数：
男生样本平均值（x̄₁）：82 分
男生样本方差（s²₁）：56 分²
男生样本大小（n₁）：25

女生样本平均值（x̄₂）：78 分
女生样本方差（s²₂）：49 分²
女生样本大小（n₂）：16

显著性水平（α）：0.02

将检验以下零假设（H₀）：
H₀: μ₁ = μ₂

与备择假设（H₁）：
H₁: μ₁ ≠ μ₂

使用双侧检验，因为我们对男生成绩比女生高或低都感兴趣。

使用 Python 和 SciPy 库来进行双样本 t 检验并计算 p 值：

from scipy import stats

# 样本参数
x_bar1, s_squared1, n1 = 82, 56, 25
x_bar2, s_squared2, n2 = 78, 49, 16

# 双样本 t 检验
t_stat, p_value = stats.ttest_ind_from_stats(x_bar1, s_squared1 ** 0.5, n1, x_bar2, s_squared2 ** 0.5, n2)

print("--------双样本 t 检验--------")
print("t值为:", t_stat)
print("p值为:", p_value)

alpha = 0.02
if p_value < alpha:
    print("拒绝原假设，均值之间存在显着差异。")
else:
    print("未能拒绝零假设，均值之间没有显着差异。")