目录
一,树和二叉树
1.树
①定义
②关于树的一些概念
2.二叉树
①定义
②特殊的二叉树
③二叉树的性质
④二叉树的存储结构(顺序结构,只适用于完全二叉树)
⑤二叉树的遍历
二,二叉树操作代码
1.头文件
2.函数代码
①创建二叉树
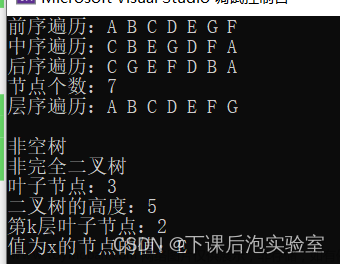
②前序遍历二叉树
③中序遍历二叉树
④后序遍历二叉树
⑤层次遍历二叉树
一,树和二叉树
1.树
①定义
树的存储结构是层次结构,即一对多的数据结构,每棵树都有一个根结点,和若干个子结点与没有子节点的叶结点。树的定义:
树(Tree)是n(n≥0)个结点的有限集合。n=0时称为空树。在任意
一棵非空树中:(1)有且只有一个特定的称为根(Root)的结点;
(2)当n>1时,其余节点可分为m(m>0)个互不相交的有限集T1,T2
,Tm,其中每一个集合本身又是一棵树,并且称为根的子树;

其中有子树T1:以结点B为子树根节点;有子树T2,以结点C为根节点。


②关于树的一些概念
度:结点拥有多少子树,结点的度就是多少;树的度为树内结点中度的最大值。
结点关系:结点称作双亲,结点的子节点称作孩子,根结点只作为双亲,叶结点只作为孩子。
层次:结点的层次从根开始定义,根为第一层,根下的子结点为第二层,然后依次向下排,叶结点为最后一层;树的结点的最大层次为树的深度或称高度。
叶结点:度为0的结点。
分支节点:度不为0的结点。
内部节点:除根和叶以外的结点。
2.二叉树
①定义
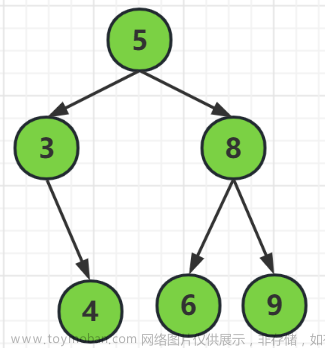
如果一棵树的每个结点的度最大为2,且结点的孩子是严格左右区分的,那么它就是一个二叉树。二叉树的定义:
二叉树是n(n≥0)个结点的有限集合,该集合或者为空集(空二叉树),
或者由一个根结点和两棵互不相交的,分别称为根结点的左子树和
右子树的二叉树组成。
上图所示的树就是一个二叉树。
②特殊的二叉树
二叉树中有两种比较特殊的,分别为完全二叉树和满二叉树;
满二叉树,顾名思义:树中所有的分支结点都存在左子树和右子树,所有的叶子都在同一层上,这样的树叫做满二叉树。
完全二叉树理解起来相对来说比较困难,但是我们只需要记住完全二叉树的特点,不必要去深究为什么这样就是完全二叉树;
完全二叉树中,结点得度不一定都是2,它的叶结点只能出现在最下面两层,也就是说最下面两层才能有度小于2的结点,且最下面一层的叶结点必须都位于左侧位置;如果倒数第二层有叶子结点,必须都是右侧子树。
③二叉树的性质
性质1:二叉树的第k层(k≥1)上最多有个结点。
性质2:二叉树高度为k,该二叉树中结点最多时有个,高度为k的完全二叉树结点最小有个。
性质3:在任意一个二叉树中,令等于度为0结点的数量,令等于度为1的结点数量,令等于度为2的结点数量,设该二叉树的总结点为,各结点数量之间有如下关系:
;
;
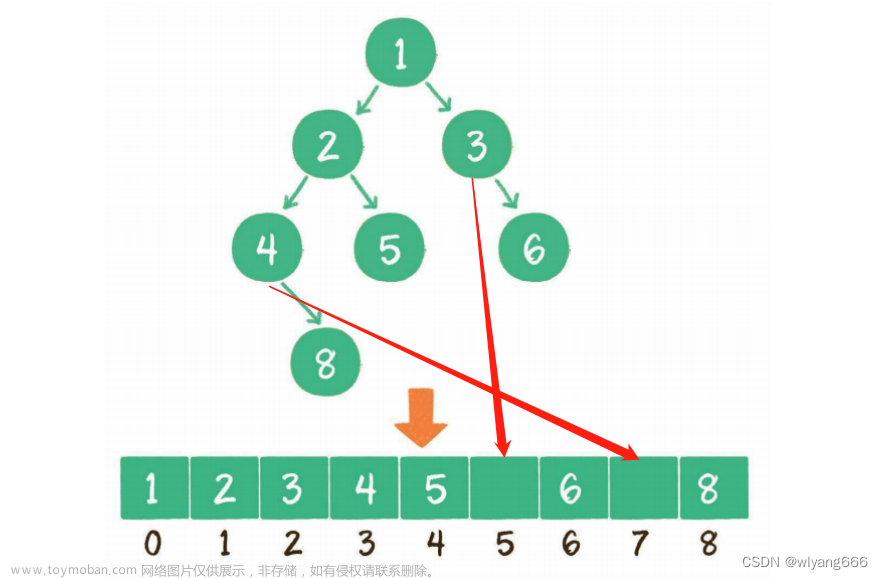
④二叉树的存储结构(顺序结构,只适用于完全二叉树)
完全二叉树结点的编号方法是从上到下,从左到右;如下两图:


结点与结点之间的编号关系一目了然;
⑤二叉树的遍历
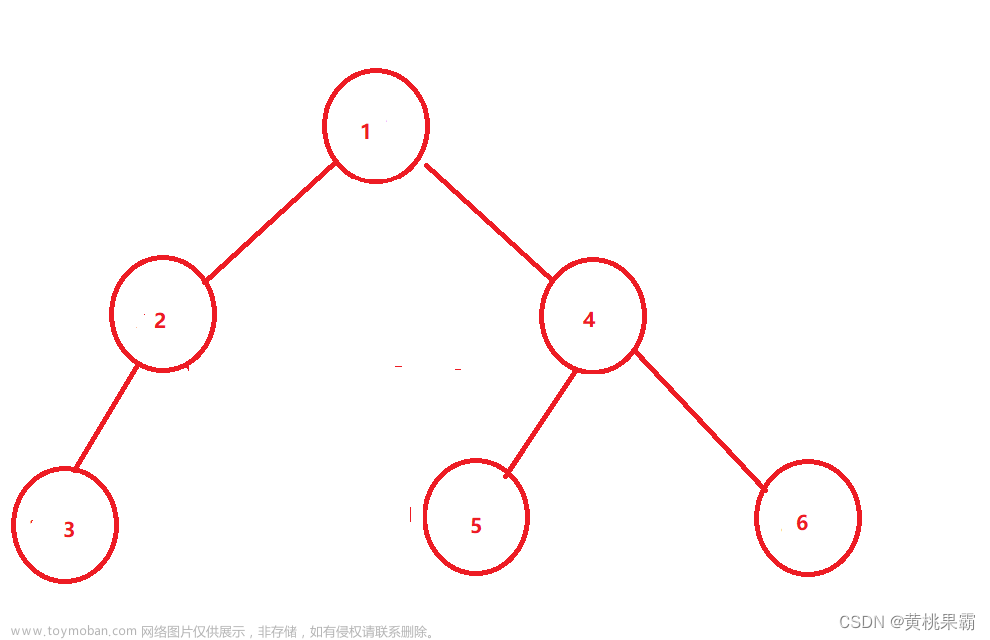
前序遍历:根->左->右;
以上图为例:从根节点开始->输出A,然后找到左子树->输出B,再以B为子根,找到B的左子树->输出D,再以D为子根,找到D的左子树->输出H,然后找到D的右子树->输出I,同样的输出E;
然后到根A的右子树C,同样循环上述操作,右侧输出为CFJG;
总输出顺序为:A-B-D-H-I-E-C-F-J-G;
中序遍历:左->根->右;
通过顺序A->B->D->H,找到最左的H,并输出H,然后返回,输出H的子根D,然后找到D的右子树I并输出,然后继续输出D的子根B,找到B的右子树E并输出,然后找到B的根A并输出;
然后找根A的右子树C,然后通过顺序C->F->J找到J,并对右侧进行相同操作;
最后输出为:H-D-I-B-E-A-J-F-C-G;
通过中序遍历可以清楚的得出结点的左右位置;

后序遍历:左->右->根;
同样的,通过顺序A->B->D->H,找到最左的H,并输出H,然后返回输出H的同层次同根的结点I并输出,最后输出子根D,继续找D的同层次同子根结点E并输出,最后再输出子根B,然后找到与B同层次同根的结点C,然后通过C->F->J的顺序找到J,并重复上述操作;
最后的输出顺序:H-I-D-E-B-J-F-G-C-A;
二,二叉树操作代码
1.头文件
二叉树中除了根结点和叶结点以外,其他结点都具有左子树(lchild)或右子树(rchlid),并且所有的结点都需要一个区域来存储数据,由此我们可以设计出二叉树的结构体;
typedef char tree_datatype;
typedef struct tree_t
{
tree_datatype data; //数据域
struct tree_t *lchild; //指向左子树的结构体指针
struct tree_t *rchild; //指向右子树的结构体指针
}bitree_t;2.函数代码
①创建二叉树
二叉树的创建和遍历都需要用到函数的递归思想;
输入时,输入连续的字符串,可以理解为,先把二叉树的左侧部分的结点的左子树从上到下,全部创建完之后(叶结点输入#时表示无子树),再从下到上创建左侧部分结点的右子树,然后创建右侧部分结点的左子树,最后创建右侧部分结点的右子树。
//1.创建一个树
bitree_t *CreateBitree(void)
{
char ch;
bitree_t *r = NULL;
scanf("%c",&ch);
if(ch == '#')
{
return NULL;
}
r = (bitree_t *)malloc(sizeof(bitree_t));
if(NULL == r)
{
printf("create fail\n");
}
r->data = ch;
r->lchild = CreateBitree();
r->rchild = CreateBitree();
return r;
}②前序遍历二叉树
首先传入树的首地址,判断是否为空,非空则输出数据,然后循环本函数遍历左子树,根据前序遍历的特点:“根->左->右”,进行遍历输出;
//2.前序遍历树
void PreShowBitree(bitree_t *r)
{
if(r == NULL)
{
return;
}
printf("%c",r->data);
PreShowBitree(r->lchild);
PreShowBitree(r->rchild);
}③中序遍历二叉树
首先传入树的首地址,判断是否为空,非空则循环本函数遍历左子树,根据中序遍历的特点:“左->根->右”,进行遍历输出;
//3.中序遍历树
void midShowBitree(bitree_t *r)
{
if(r == NULL)
{
return;
}
midShowBitree(r->lchild);
printf("%c",r->data);
midShowBitree(r->rchild);
}④后序遍历二叉树
首先传入树的首地址,判断是否为空,非空则循环本函数遍历左子树,根据后序遍历的特点:“左->右->根”,进行遍历输出;
//4.后序遍历树
void PostShowBitree(bitree_t *r)
{
if(r == NULL)
{
return;
}
PostShowBitree(r->lchild);
PostShowBitree(r->rchild);
printf("%c",r->data);
}⑤层次遍历二叉树
层次遍历即从上到下,从左到右进行输出;
层次遍历需要使用学习队列时的函数,先让根结点入队,循环内先让根结点出队,然后让根结点的左子树入队,右子树入队,然后左子树出队,左子树的左子树入队,左子树的右子树入队,然后右子树出队,右子树的左子树和右子树分别入队,然后进行循环,直到队列为空,循环结束;文章来源:https://www.toymoban.com/news/detail-428592.html
//5.层次遍历
void levelShowBitree(bitree_t *r)
{
if (r == NULL)
{
return;
}
//创建队列
queue_t *p = CreateQueue();
//根节点入队
IntoQueue(p,r);
while(!isEpQueue(p))
{
//节点出队
r = OutQueue(p);
printf("%c",r->data);
if(r->lchild != NULL)
{
IntoQueue(p,r->lchild);
}
if(r->rchild != NULL)
{
IntoQueue(p,r->rchild);
}
}
}如果本文中存在代码逻辑,代码完善,解释不通或不清楚的错误,还请批评指正。文章来源地址https://www.toymoban.com/news/detail-428592.html
到了这里,关于数据结构之二叉树(C语言附详细代码)的文章就介绍完了。如果您还想了解更多内容,请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章,希望大家以后多多支持TOY模板网!