二叉树的遍历及相关衍生-Toy模板网

这篇具有很好参考价值的文章主要介绍了二叉树的遍历及相关衍生。希望对大家有所帮助。如果存在错误或未考虑完全的地方，请大家不吝赐教，您也可以点击"举报违法"按钮提交疑问。

前言

如标题所示，在这里我们要研究的是二叉树的遍历。

为什么不讲二叉树的增删查改？
在实际使用过程中，二叉树的增删查改没有多大作用，二叉树是作为一种数据结构，不是用来存储数据，更多的是用来进行搜索

赫赫有名的红黑树和B树，都是其的限制优化的产物之一。

但是身为小白的博主现在只能先从最基本的遍历开始玩起。

博主刚学C++一点，为了练习和熟悉，所以用的是C++，但是也没多熟练，还是有C的老习惯，请各位多多海涵

二叉树的遍历

建树

我们想要学习对树的遍历，首先就要有一颗树。

所以我们先要进行一次快速的建树
二叉树的遍历及相关衍生
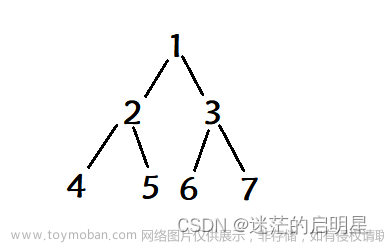
我们要建立这样一颗树

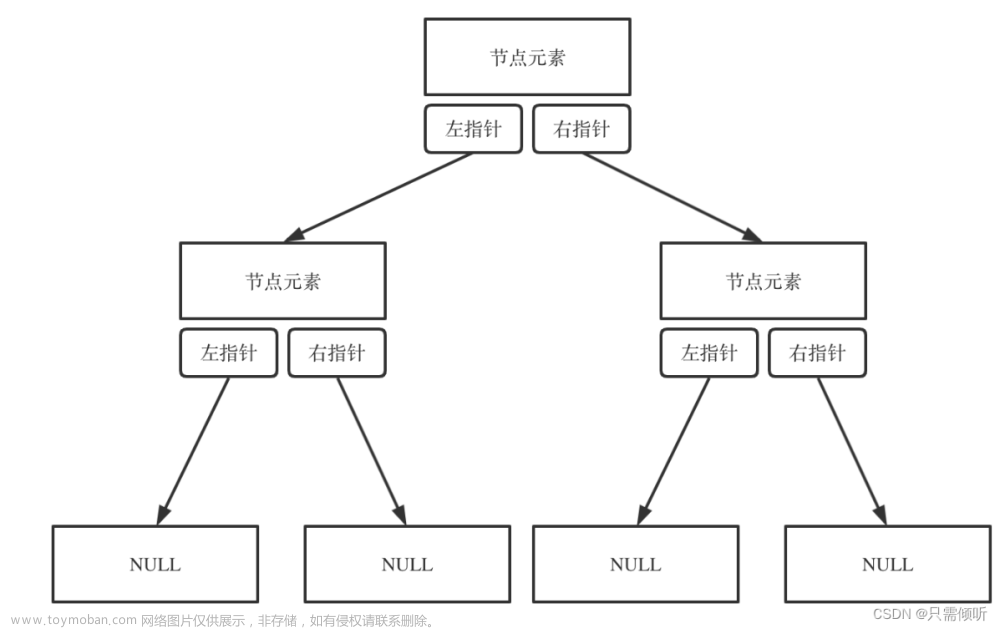
可以看出我们在设计类的变量时，需要设置三个
1：存储数据的int
2：存放右子节点的指针
3：存放左子节点的指针

class tree
{
public:
	tree* inittree(int x, tree* left, tree* right)
	{
		tree* ptr = (tree*)malloc(sizeof(tree));
		assert(ptr);
		ptr->_data = x;
		ptr->_left = left;
		ptr->_right = right;
		return ptr;
	}
private:
	int _data;
	tree* _left;
	tree* _right;
};
int main()
{
	tree t1;
	tree* ptr3=t1.inittree(3, nullptr, nullptr);
	tree* ptr2=t1.inittree(2, ptr3, nullptr);
	tree* ptr6 = t1.inittree(6, nullptr, nullptr);
	tree* ptr5 = t1.inittree(5, nullptr, nullptr);
	tree* ptr4 = t1.inittree(4, ptr5, ptr6);
	tree* ptr1 = t1.inittree(1, ptr2, ptr4);
}

没错，建树就是这么简单直接，因为我们主要来学习他的遍历，所以建树这些繁琐的事情快速解决就好了。

二叉树的遍历

看名字，所谓遍历，就是将二叉树中的数据全部访问一遍

二叉树的遍历及相关衍生
如果我们要实现这颗二叉树的遍历，想必大家都多少听过，二叉树和递归算法脱不了一点关系。

虽然有些人听到递归就有点小怕，但是如果把思路理解了以后，递归可比迭代快太多了。

当我们进行遍历的时候，有这样三种操作

1：访问根，就是遍历的历，对根存储的数据进行访问。
2：走向左子树，
3：走向右子树
二叉树的遍历及相关衍生
设计的都是先访问左子树，再访问右子树
这应该是约定俗成的把，虽然先右到左也没什么区别，但是从左往右还是看着赏心悦目一点。

所以纠结的只有根的访问顺序，这样就牵扯到遍历的差别了。

遍历的分类

前根遍历
顾名思义，就是先根后左右
先根后左右
这里我们先将
1：访问根
2：访问左子树
3：访问右子树
这样设定好
二叉树的遍历及相关衍生

因为递归是对函数的重复调用，作用对象是每一个节点，所以到了左子树的节点后，要对子节点进行同样与根节点的操作
即先访问节点数据，在进行左子树和右子树的访问。

这里为了方便看清，就在第一个第二个第三个节点加了前缀，1.1就是第一个节点访问根。

这里当第三个节点访问左右子树为空后，直接进行返回。

剩下两个遍历类型为

中根遍历

即先访问左子树，访问根，再访问右子树

后根遍历

即先访问左右子树，再访问根。

就不多讲了。

代码部分

void Traversaltree(tree* root)
	{
		if (root == nullptr)
		{
			cout << " NULL";
			return;
		}
		//访问根的部分按照遍历存放
		//访问根的代码按照具体情况而定

//访问根放这-前根
		printtree(root->_left);
//访问根放这-中根
		printtree(root->_right);
//访问根放这-后根
	}

遍历根的应用

打印树中的每个数据

由于我们这个二叉树不是完全二叉树这种特殊树，所以用数组打印时，就会导致残缺不堪
二叉树的遍历及相关衍生
就比如打印这颗树

代码部分

void printtree(tree* root)
	{
		if (root == nullptr)
		{
			cout << " NULL";
			return;
		}
		//前根遍历打印
		cout << " " << root->_data; 
		printtree(root->_left);
		printtree(root->_right);
	}

遍历计算树节点个数

代码部分

	int  sizetree(tree* root)
	{
		if (root == nullptr)
			return 0;
		return sizetree(root->_left)
		 + sizetree(root->_right) + 1;

	}

按照代码画图

二叉树的遍历及相关衍生
先是通过sizetree(root->_left)，从根节点不断访问左子树，然后节点继续访问它的左子树,直到节点的左子树为空。
当访问到3节点时，在进行左子树为NULL后返回0

随后执行sizetree(root->_right)，对3节点的右子树进行访问，为空，返0。

执行return sizetree(root->_left) + sizetree(root->_right) + 1;
返回 {（左子树的返回）0+（右子树的返回）0 + 1=1}

这个时候重新返回了2节点，
二叉树的遍历及相关衍生

对于二节点，收到了左子树的返回1，右子树为空，返回0

返回给1节点的访问左子树的返回值为
（2节点访问左子树返回值） 1+（2节点访问左子树返回值） 0 +1=2

解释到这，就可以推测出整个递归运行的逻辑了。

计算二叉树的深度

故名思义，就是计算二叉树的深度。

为了更能体现作用，所以将之前的树重新接了一下
二叉树的遍历及相关衍生

思路

这里我们采用直接思考解决方法，直接写代码
不通过想象它的一次一次递归的执行方式去写代码
这样更加快速，当然等会还是会解释递归的执行思路的。

这里我们先不看整个二叉树，我们先来看，对于单一的一个子节点来说
当它接收到来自左边和右边的深度后
将右边和左边的深度进行比较
如果左边较大，则返回左边深度+1值
如果右边较大，则返回右边深度+1值

为什么要+1？
因为返回深度的话还要把自己的深度+1

这样我们就可以试着写出一个代码了

if (root == nullptr)
     return 0;
return heighttree(root->_left) > 
heighttree(root->_right)
?
 heighttree(root->_left) + 1 
:
 heighttree(root->_right) + 1;

这样运行一下，发现还真可以计算，但是如果你深度进行观察这个代码，就会发现这个写法太挫了
当我们进行比较后，不停进行右子树和左子树访问后

在进行三目操作符执行后，居然还要进行左子树和右子树的访问，这样时间复杂度直接从On变到了On^2

其实要解决这个问题也很简单，加个计数的就好，接下来的是最优的代码。

代码部分

int heighttree(tree* root)
	{
		if (root == nullptr)
			return 0;
		int left=heighttree(root->_left);
		int right=heighttree(root->_right);
		return left > right ? left + 1 : right + 1;	
	}

二叉树的遍历及相关衍生

首先不断执行int left=heighttree(root->_left);

不停访问左子树，到节点3时，左子树为空
赋值int left=0，之后执行int right=heighttree(root->_right);

访问到6节点，再执行6的左子树访问，到5节点

5节点左右为空，left right皆为0
进行三目操作符比较后，执行return right+1

此时回到6节点
6节点的左子树访问返回，进行赋值int left=1
右子树为空，所以int right=0
进行三目操作符比较后，执行return left+1

返回到 3节点
得到int right=2
与left=0进行比较，返回right+1

…………
解释了两个三个节点操作过程就可以看出整个的递归逻辑了。

第k层个数

顾名思义，给定一个k，求第k层有几个节点

这里直接上代码了，因为难度和前面大差不差

//第k层个数
	int treeklevel(tree* root,int k)
	{
		if (root == nullptr)
			return 0;
		if (k == 1)
			return 1;
		return treeklevel(root->_left,k-1) 
		+ treeklevel(root->_right,k-1);
	}