目录
前言
一、数字旋转方阵
二、实验内容
三、实验目的
四、实验步骤
五、实验过程
总结
前言
算法同样是计算机四大件的一个很重要的内容,本实验的目的是通过编写一个数字旋转方阵程序,来掌握分治与减治算法的基本思想和实现方法。
一、数字旋转方阵
数字旋转方阵是一个n×n的矩阵,其中每个元素是从1到n^2的自然数,且按照顺时针旋转的方式排列。例如,当n=4时,数字旋转方阵如下:
1 2 3 4
12 13 14 5
11 16 15 6
10 9 8 7
本实验要求使用分治或减治算法来设计一个高效的数字旋转方阵程序,并分析其时间复杂度和空间复杂度。同时,要求使用适当的数据结构来存储和输出数字旋转方阵,以及提供一个友好的用户界面,让用户可以输入n的值,并查看生成的数字旋转方阵。
二、实验内容
给出一个初始数据,在此数据的基础上由外层向里层填写数据,完成一个数字旋转方阵,输出结果,输出时要求有文字说明。请任选一种语言编写程序实现上述算法,并分析其算法复杂度。
本文中所使用语言是c++
三、实验目的
(1)掌握分治法的设计思想;
(2)掌握数字旋转方阵的具体实现过程;
(3)熟练掌握二维数组的使用方法;
(4)在掌握的基础上编程实现数字旋转方阵的实现过程
四、实验步骤
(1)根据实验内容设计算法伪代码进行算法描述;
(2)利用C++/C/Java等编程语言对算法伪代码进行工程化实现;
(3)输入测试用例对算法进行验证;
(4)列出算法时间复杂度模型并与计算机运行统计时间进行对比分析。
五、实验过程
1、算法分析
数字旋转方阵算法是一种填充数字的算法,它可以将数字填充到一个旋转的矩阵中。该算法的实现过程如下:
- 声明二维数组a ,size为需建立的方阵阶数,初始化i,j,num为1
- 若size=0,则循环结束;
- 若size=1,则使a [i] [j]=num,循环结束;
- 填写区域A,重复操作size-1次
- a [i] [j]=num;i++;num++;
- 填写区域B,重复操作size-1次
- a [i] [j]=num;j++;num++;
- 填写区域C,重复操作size-1次
- a [i] [j]=num;i–;num++;
- 填写区域D,重复操作size-1次
- a [i] [j]=num;j–;num++;
- i++;j++;size=size-2;
- 返回第1步;
- 循环结束后,输出数组a;
该算法的时间复杂度为O(n^2),其中n为方阵的阶数。该算法可以用于填充数字到一个旋转的矩阵中。例如,我们可以使用该算法来生成一个螺旋状的数字矩阵。
2、写出伪代码
声明二维数组a ,size为需建立的方阵阶数,初始化i,j,num为1
若size=0,则循环结束;
若size=1,则使a [i] [j]=num,循环结束;
填写区域A,重复操作size-1次
a [i] [j]=num;i++;num++;
填写区域B,重复操作size-1次
a [i] [j]=num;j++;num++;
填写区域C,重复操作size-1次
a [i] [j]=num;i--;num++;
填写区域D,重复操作size-1次
a [i] [j]=num;j--;num++;
i++;j++;size=size-2;
返回第1步;
循环结束后,输出数组a;3、代码实现
#include <iostream>
#include <iomanip>
using namespace std;
void NFangZhen (int n) {
int size=n;
int flag=0; //设置转换方向标志
int a [100] [100]; //设置二维数组
int i=0,j=0,num=1;
while (1) {
if (size==0) break;
else if (size==1) {
a [i] [j]=num;
break;
}
else {
do //区域A
{
a [i] [j]=num;
i++;
num++;
flag++;
}while (flag<size-1);
flag=0;
do //区域B
{
a [i] [j]=num;
j++;
num++;
flag++;
}while (flag<size-1);
flag=0;
do //区域C
{
a [i] [j]=num;
i--;
num++;
flag++;
}while (flag<size-1);
flag=0;
do //区域D
{
a [i] [j]=num;
j--;
num++;
flag++;
}while (flag<size-1);
flag=0;
}
size-=2;
i++;
j++;
}
for (int i=0;i<n;i++) {
for (int j=0;j<n;j++) {
cout<<setw(4)<<a [i] [j]<<" ";
}
cout<<endl;
}
}
int main () {
int n;
cout<<"请输入数字旋转方阵的阶数:";
cin>>n;
NFangZhen(n);
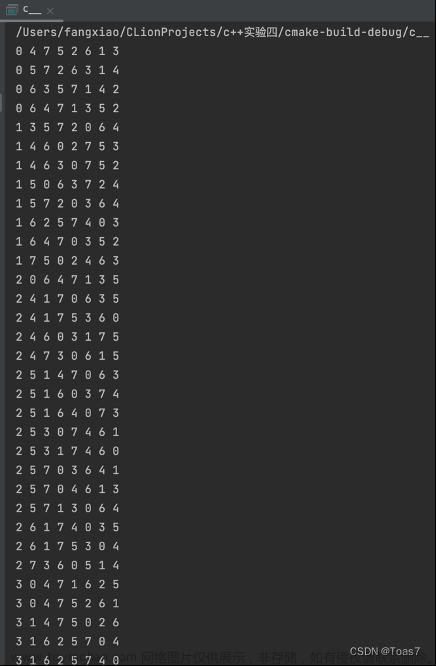
}4、用例测试

5、分析复杂度
数字旋转方阵算法的时间复杂度为O(n2),其中n为方阵的阶数。这是因为该算法需要填充n2个数字到一个n*n的矩阵中,每个数字都需要执行一次赋值操作,因此总共需要执行n2次赋值操作。因此,该算法的时间复杂度为O(n2)文章来源:https://www.toymoban.com/news/detail-429017.html
总结
这篇文章是数字旋转方阵程序设计的实验报告。文章介绍了数字旋转方阵的存储结构和算法设计。程序采用二维数组的存储结构进行数字旋转方阵的存储,每一层的数字分作四个小组,每一组的数字个数为N-1,通过设立一个标志来判断转换方向。文章来源地址https://www.toymoban.com/news/detail-429017.html
到了这里,关于算法设计与分析实验:分治与减治算法实验:题目1 数字旋转方阵程序设计的文章就介绍完了。如果您还想了解更多内容,请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章,希望大家以后多多支持TOY模板网!