图的邻接表
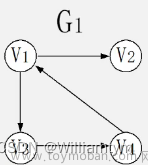
我们重点分析一下无向图
邻接表
我们如何将图中所有顶点和边建立起联系?
1.我们发现,V0这个顶点与V1和V3相连,通过右边的邻接表可以看到会出现一个以 V0为头结点的单链表,后面连接的元素就是V1和V3 在顶点数组中的下标
2.这里解释下顶点数组 ,我们事先定义一个数组,用于存放所有的顶点{V0,V1,V2,V3,V4},后期就可以通过下标去找到顶点(每个单链表的头结点)进行 遍历操作
代码实现
step1.创建邻接表的结构体

#define _CRT_SECURE_NO_WARNINGS
#include<stdio.h>
#include<stdlib.h>
#define MaxV 20
//创建邻接表的结构体
typedef struct ArcNode {//边结点
int adjvex;//该边所指向的顶点在数组中的位置
struct ArcNode* nextarc;//指向下一条边的指针
}ArcNode;
typedef struct VNode {//顶点信息(顶点作为每个单链表的表头结点)
int data;
ArcNode* firstarc;//指向第一条依附该顶点的边的指针
}AdjList[MaxV];
typedef struct {
AdjList vertices;
int vexnum, arcnum;//图的当前顶点数和边数
int kind;//f分成无向图和有向图
}ALGraph;
step2.初始化邻接表
1.首先给出顶点数和边数
2.对于每条边,都会关联两个顶点,所以接下里输入被关联的两个顶点
3.通过输入的顶点调用LocateVex函数来找到这两个顶点在顶点数组中的下标
4.创建新结点,采用头插法插入到以每个顶点为头结点的单链表中
5.此处的kind如果为0,那就是无向图,否则均为有向图
void InitALGraph(ALGraph* G,int vexnum,int arcnum) {//顶点个数和边数
G->vexnum = vexnum;
G->arcnum = arcnum;
for (int i = 0; i < G->vexnum; i++) {//给顶点赋值,建立表头结点
scanf("%d" ,& G->vertices[i].data);
G->vertices[i].firstarc = NULL;
}
for (int k = 0; k < G->arcnum; k++) {
int v1 = 0;//每条边关联两个顶点
int v2 = 0;
scanf("%d%d", &v1, &v2);
int i = LocateVex(G, v1);
int j = LocateVex(G, v2);//(i,j)即为对应顶点在vertices数组中的位置
ArcNode* newNode1 = (ArcNode*)malloc(sizeof(ArcNode));
newNode1->adjvex = j;
newNode1->nextarc = G->vertices[i].firstarc;//头插法
G->vertices[i].firstarc = newNode1;
//对称
if (G->kind == 0) {//无向图
ArcNode* newNode2 = (ArcNode*)malloc(sizeof(ArcNode));
newNode2->adjvex = i;
newNode2->nextarc = G->vertices[j].firstarc;//头插法
G->vertices[j].firstarc = newNode2;
}
}
}
step3.实现LocateVex函数
int LocateVex(ALGraph* G, int u)
{
/* 初始条件: 图G存在,u和G中顶点有相同特征*/
/* 操作结果: 若G中存在顶点u,则返回该顶点在图中位置;否则返回-1 */
for (int i = 0; i < G->vexnum; ++i) {
if (u == G->vertices[i].data) {
return i;
}
}
return -1;
}
step4.写出打印函数,测试是否正确
void printALGraph(ALGraph* G) {
int v = 0;
for (v = 0; v < G->vexnum; v++) {//遍历所有的顶点,分别遍历每个顶点的单链表
printf("%d ", G->vertices[v].data);
ArcNode* p;
for (p = G->vertices[v].firstarc; p; p = p->nextarc) {
printf("%d ", G->vertices[p->adjvex].data);
}
printf("\n");
}
}
step5.main函数
int main() {
int vexnum;
int arcnum;
ALGraph* G = (ALGraph*)malloc(sizeof(ALGraph));
scanf("%d%d", &vexnum, &arcnum);
int kind = 0;
scanf("%d", &kind);
G->kind = kind;
InitALGraph(G, vexnum, arcnum);
printf("===========\n");
printALGraph(G);
return 0;
}


后面连接顺序不完全一样是输入顺序导致的,但不想影响最后结果,测试是成功的
5个顶点,6条边
0表示无向图
0 1 2 3 4表示顶点信息
0 3表示0和3有一条关联边,下面以此类推


完整代码如下文章来源:https://www.toymoban.com/news/detail-429445.html
#define _CRT_SECURE_NO_WARNINGS
#include<stdio.h>
#include<stdlib.h>
#define MaxV 20
//创建邻接表的结构体
typedef struct ArcNode {//边结点
int adjvex;//该边所指向的顶点在数组中的位置
struct ArcNode* nextarc;//指向下一条边的指针
}ArcNode;
typedef struct VNode {//顶点信息(顶点作为每个单链表的表头结点)
int data;
ArcNode* firstarc;//指向第一条依附该顶点的边的指针
}AdjList[MaxV];
typedef struct {
AdjList vertices;
int vexnum, arcnum;//图的当前顶点数和边数
int kind;//f分成无向图和有向图
}ALGraph;
int LocateVex(ALGraph* G, int u)
{
/* 初始条件: 图G存在,u和G中顶点有相同特征*/
/* 操作结果: 若G中存在顶点u,则返回该顶点在图中位置;否则返回-1 */
for (int i = 0; i < G->vexnum; ++i) {
if (u == G->vertices[i].data) {
return i;
}
}
return -1;
}
void InitALGraph(ALGraph* G,int vexnum,int arcnum) {//顶点个数和边数
G->vexnum = vexnum;
G->arcnum = arcnum;
for (int i = 0; i < G->vexnum; i++) {//给顶点赋值,建立表头结点
scanf("%d" ,& G->vertices[i].data);
G->vertices[i].firstarc = NULL;
}
for (int k = 0; k < G->arcnum; k++) {
int v1 = 0;//每条边关联两个顶点
int v2 = 0;
scanf("%d%d", &v1, &v2);
int i = LocateVex(G, v1);
int j = LocateVex(G, v2);//(i,j)即为对应顶点在vertices数组中的位置
ArcNode* newNode1 = (ArcNode*)malloc(sizeof(ArcNode));
newNode1->adjvex = j;
newNode1->nextarc = G->vertices[i].firstarc;//头插法
G->vertices[i].firstarc = newNode1;
//对称
if (G->kind == 0) {//无向图
ArcNode* newNode2 = (ArcNode*)malloc(sizeof(ArcNode));
newNode2->adjvex = i;
newNode2->nextarc = G->vertices[j].firstarc;//头插法
G->vertices[j].firstarc = newNode2;
}
}
}
void printALGraph(ALGraph* G) {
int v = 0;
for (v = 0; v < G->vexnum; v++) {//遍历所有的顶点,分别遍历每个顶点的单链表
printf("%d ", G->vertices[v].data);
ArcNode* p;
for (p = G->vertices[v].firstarc; p; p = p->nextarc) {
printf("%d ", G->vertices[p->adjvex].data);
}
printf("\n");
}
}
int main() {
int vexnum;
int arcnum;
ALGraph* G = (ALGraph*)malloc(sizeof(ALGraph));
scanf("%d%d", &vexnum, &arcnum);
int kind = 0;
scanf("%d", &kind);
G->kind = kind;
InitALGraph(G, vexnum, arcnum);
printf("===========\n");
printALGraph(G);
return 0;
}
有些东西看起来很复杂,但仔细一想,不过都是我们学过的东西,需要你耐心发现!!!文章来源地址https://www.toymoban.com/news/detail-429445.html
到了这里,关于【C语言】图的邻接表——超详细解析的文章就介绍完了。如果您还想了解更多内容,请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章,希望大家以后多多支持TOY模板网!