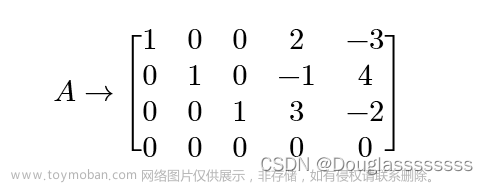
1、线性方程组的最小二乘解
对于线性方程组求解,我们一般写成矩阵形式 Ax = y。

当矩阵A满秩(即这q个变量是线性无关的)时:
p<q 时,为欠定方程组,方程个数少于未知数个数,有多解;
p=q 时,为方阵,方程个数等于未知数个数,有唯一解;
p>q 时,为超定方程组,方程个数多于未知数个数,无解(除非y可以由A的列向量线性表示);
我们实际中,需要使用多个方程组,以降低噪声对求解过程的影响,得到近似最优解。p>q时,定义误差函数E(x):

线性方程组的最小二乘解为:

有以下三种求解方法:

方法1,需要求解A的逆,计算量大。方法2,不用求逆。方法三需要迭代。所以一般,选择方法2。
2、齐次线性方程组的最小二乘解
齐次线性方程组的特点是右边表达式全为0,写成矩阵形式为 Ax = 0。

当矩阵A满秩时:
p<q 时,为欠定方程组,方程个数少于未知数个数,有多解;
p=q 时,方程个数等于未知数个数,只有零解;
p>q 时,为超定方程组,方程个数多于未知数个数,除零解外无解;
PS:如果 x 是方程组的解,对于任意 k != 0,kx也是方程组的解。
当 p>q是时,定义误差函数 E(x):

齐次方程的最小二乘解,为了求解唯一值,增加约束 ||x||=1 ,所以齐次方程解与真实解永远相差一个放大系数:

求解方法(奇异值分解):

PS:或者拉格朗日求解。
3、非线性方程组的最小二乘解
一般系统,有 p 个方程,q 个变量。f 为非线性函数。

当 p > q 时的最小二乘解:

解法:牛顿法与列文伯格-马夸尔特法(L-M方法)
1)从初始解开始迭代,若初始解与实际相距较远,可能会很慢;
2)估计解可能是初始解的函数(由于局部最小值);
3)牛顿法需计算一阶段到矩阵J(雅克比矩阵),二阶导矩阵H(海塞矩阵);
4)L-M算法不用计算H。文章来源:https://www.toymoban.com/news/detail-429458.html
实际中使用时,有现成的包可以调用,不用担心计算过程。文章来源地址https://www.toymoban.com/news/detail-429458.html
到了这里,关于方程组的最小二乘解的文章就介绍完了。如果您还想了解更多内容,请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章,希望大家以后多多支持TOY模板网!