😛作者:日出等日落
📘 专栏:数据结构
抱怨是一件最没意义的事情。如果实在难以忍受周围的环境,那就暗自努力练好本领,然后跳出那个圈子。
目录
🎄二叉树
✔二叉树的结构:
✔BuyNode(创建二叉树节点):
🎄基本函数操作:
✔PreOrder(前序递归遍历):
✔InOrder(中序递归遍历):
✔PostOrder(后序递归遍历):
✔TreeSize(函数结点个数):
✔TreeleafSize(叶子结点个数):
✔TreeHeight(树的深度/高度):
✔TreeKLevelSize(第k层的结点个数):
✔TreeFind(二叉树查找值为x的值):
✔LevelOrder(层序遍历):
✔TreeComplete(判断二叉树是否是完全二叉树):
✔TreeDestory(二叉树销毁):
🎄二叉树
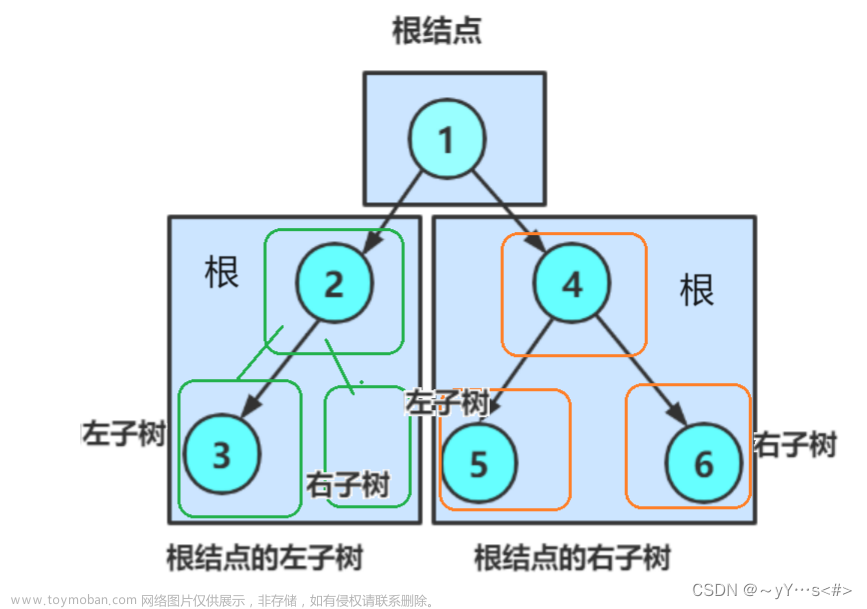
二叉树(Binary tree)是树形结构的一个重要类型。许多实际问题抽象出来的数据结构往往是二叉树形式,即使是一般的树也能简单地转换为二叉树,而且二叉树的存储结构及其算法都较为简单,因此二叉树显得特别重要。二叉树特点是每个节点最多只能有两棵子树,且有左右之分。
注:如需详细了解,请看详细二叉树概念博客http://t.csdn.cn/sJWfX
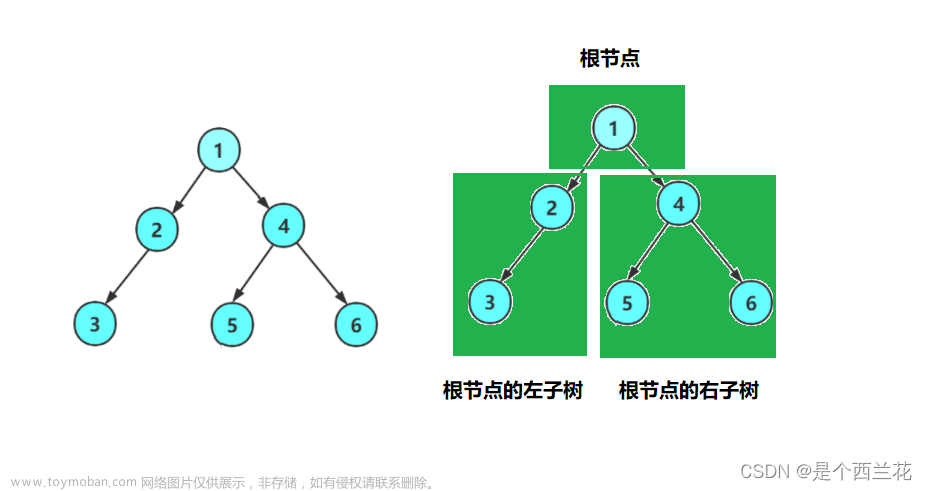
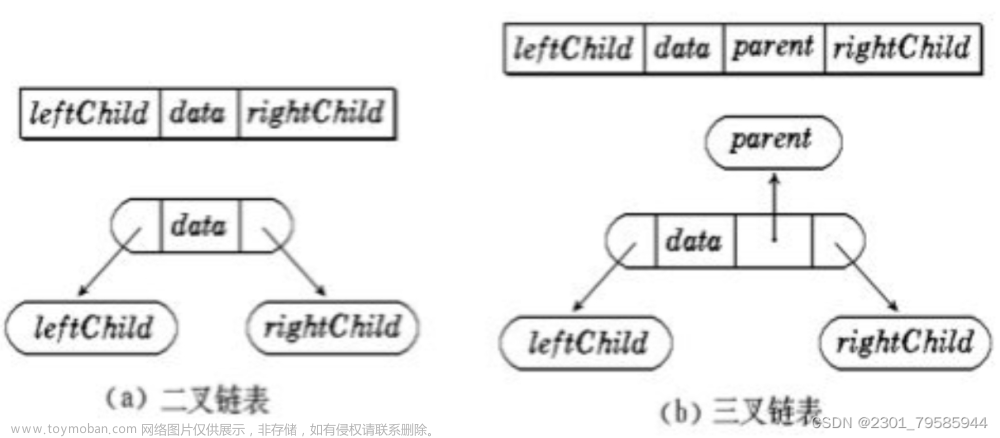
✔二叉树的结构:
二叉树是一个节点root,链接着一个左节点left和一个右节点right
typedef int BTDataType;
typedef struct BinaryTreeNode
{
BTDataType data;
struct BinaryTreeNode* left;
struct BinaryTreeNode* right;
}BTNode;
✔BuyNode(创建二叉树节点):
BTNode* BuyNode(BTDataType x)
{
BTNode* newnode = (BTNode*)malloc(sizeof(BTNode));
if (newnode == NULL)
{
perror("malloc fail:");
exit(-1);
}
newnode->data = x;
newnode->left = newnode->right = NULL;
return newnode;
}在学习二叉树的基本操作前,需先要创建一棵二叉树,然后才能学习其相关的基本操作。由于现在大家对二叉树结构掌握还不够深入,为了降低大家学习成本,此处手动快速创建一棵简单的二叉树,快速进入二叉树 操作学习,等二叉树结构了解的差不多时,我们反过头再来研究二叉树真正的创建方式。
//构造二叉树
BTNode* n1 = BuyNode(1);
BTNode* n2 = BuyNode(2);
BTNode* n3 = BuyNode(3);
BTNode* n4 = BuyNode(4);
BTNode* n5 = BuyNode(5);
BTNode* n6 = BuyNode(6);
BTNode* n7 = BuyNode(7);
n1->left = n2;
n1->right = n4;
n2->left = n3;
n3->left = n7;
n4->left = n5;
n4->right = n6;注意:上述代码并不是创建二叉树的方式,真正创建二叉树方式后序详解重点讲解。
🎄基本函数操作:
再看二叉树基本操作前,再回顾下二叉树的概念,
二叉树是:
1. 空树
2. 非空:根节点,根节点的左子树、根节点的右子树组成的。
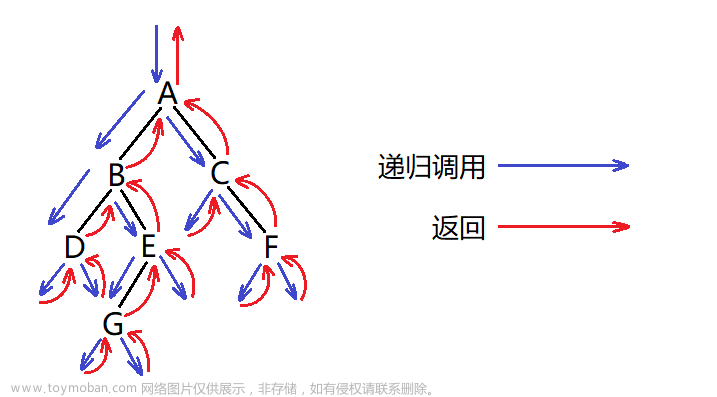
✔PreOrder(前序递归遍历):
前序遍历是每颗子树都先遍历root节点,再遍历左子树,最后在遍历右子树。
前序遍历:root 左子树 右子树
// 二叉树前序遍历
void PreOrder(BTNode* root)
{
if (root == NULL)
{
printf("NULL ");
return;
}
printf("%d ", root->data);
PreOrder(root->left);
PreOrder(root->right);
}✔InOrder(中序递归遍历):
中序遍历是每颗子树都先遍历左子树,再遍历root节点,最后在遍历右子树。
中序遍历:左子树 root 右子树
// 二叉树中序遍历
void InOrder(BTNode* root)
{
if (root == NULL)
{
printf("NULL ");
return;
}
InOrder(root->left);
printf("%d ", root->data);
InOrder(root->right);
}✔PostOrder(后序递归遍历):
后序遍历是每颗子树都先遍历左子树,再遍历右子树,最后在遍历root节点。
后序遍历:左子树 右子树 root
// 二叉树后序遍历
void PostOrder(BTNode* root)
{
if (root == NULL)
{
printf("NULL ");
return;
}
PostOrder(root->left);
PostOrder(root->right);
printf("%d ", root->data);
}
✔TreeSize(函数结点个数):
二叉树节点的个数,可以看成左子树的节点个数+右子树的节点个数+1(根节点)。
遇到NULL返回0。
//返回二叉树的结点个数
int TreeSize(BTNode* root)
{
return root == NULL ? 0 :
TreeSize(root->left) + TreeSize(root->right) + 1;
}✔TreeleafSize(叶子结点个数):
叶节点代表它没有左右节点了,也就是左右节点皆为NULL
- 当左右左右节点皆为NULL时返回1
- 叶节点数等于左子树的叶子个数+右子树的叶子个数
//返回叶子结点个数
int TreeleafSize(BTNode* root)
{
if (root == NULL)
return 0;
if (root->left == NULL && root->right == NULL)
return 1;
return TreeleafSize(root->left) + TreeleafSize(root->right);
}✔TreeHeight(树的深度/高度):
当只有一层的时候,左子树为0,右子树为0层,总层数为 1层。
当有2层时,左子树为1,右子树为1层,总层数为1+1层。
当有3层时,左子树为2,右子树为2层,总层数为2+1层。
....
当有N层时,左子树为N-1层,右子树为N1层,总层数为(N-1)+1层。
这样就可以将树的高度看成较高子树的层高+1(根节点的那一层)。因此将左右子树的层数计算出来,让他们较大的一个+1就是二叉树的高度了。
//返回树的深度
int TreeHeight(BTNode* root)
{
if (root == NULL)
return 0;
int leafHeight = TreeHeight(root->left);
int rightHeight = TreeHeight(root->right);
return leafHeight > rightHeight ? leafHeight + 1 : rightHeight + 1;
}✔TreeKLevelSize(第k层的结点个数):
可以通过左右子树,让他们可下降k-1层,k-1层的左孩子与右孩子树就是第k层的结点数
如果k==1,则返回1
如果为NULL,就返回0
//第k层的结点个数 k >= 1
int TreeKLevelSize(BTNode* root, int k)
{
if (root == NULL)
return 0;
if (k == 1)
return 1;
return TreeKLevelSize(root->left, k - 1) + TreeKLevelSize(root->right, k - 1);
}✔TreeFind(二叉树查找值为x的值):
依旧不断通过左子树和右子树分别遍历下去
找到等于x的值,就返回那个结点
遇到NULL时,返回NULL
当全部找完依旧没找到,那就返回NULL。
//二叉树查找值为x的值
BTNode* TreeFind(BTNode* root, BTDataType x)
{
if (root == NULL)
return NULL;
if (root->data == x)
return root;
BTNode* ret1 = TreeFind(root->left, x);
if (ret1)
return ret1;
BTNode* ret2 = TreeFind(root->right, x);
if(ret2)
return ret2;
return NULL;
}✔LevelOrder(层序遍历):
这里需要用到队列,队列详细讲解:http://t.csdn.cn/vhPtL文章来源:https://www.toymoban.com/news/detail-429504.html
- 先让根节点进入队列
- 将队头用一个变量保存下来,如果不为NULL就将其打印
- 再将队头pop一下
- 当左右节点存在,就将其push进去队列,以此循环
//层序遍历
void LevelOrder(BTNode* root)
{
Queue q;
QueueInit(&q);
if (root)
{
QueuePush(&q, root);
}
while (!QueueEmpty(&q))
{
BTNode* front = QueueFront(&q);
printf("%d ", front->data);
QueuePop(&q);
if (front->left)
QueuePush(&q, front->left);
if (front->right)
QueuePush(&q, front->right);
}
printf("\n");
QueueDestroty(&q);
}
✔TreeComplete(判断二叉树是否是完全二叉树):
这个是建立在层序遍历的基础上的,利用层序遍历,遍历到第一个NULL时,后面都不为NULL才为完全二叉树,如果后面有一个不为NULL,那就不是完全二叉树返回false。文章来源地址https://www.toymoban.com/news/detail-429504.html
// 判断二叉树是否是完全二叉树
bool BinaryTreeComplete(BTNode* root)
{
Queue q;
QueueInit(&q);
if (root)
{
QueuePush(&q, root);
}
while (!QueueEmpty(&q))
{
BTNode* front = QueueFront(&q);
QueuePop(&q);
if (front == NULL)
{
break;
}
else
{
QueuePush(&q,front->left);
QueuePush(&q,front->right);
}
}
while (!QueueEmpty(&q))
{
BTNode* front = QueueFront(&q);
QueuePop(&q);
if (front != NULL)
{
QueueDestroty(&q);
return false;
}
}
QueueDestroty(&q);
return true;
}
✔TreeDestory(二叉树销毁):
// 二叉树销毁
void TreeDestory(BTNode* root)
{
if (root == NULL)
return;
TreeDestory(root->left);
TreeDestory(root->right);
free(root);
}
到了这里,关于【数据结构】二叉树(链式)的文章就介绍完了。如果您还想了解更多内容,请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章,希望大家以后多多支持TOY模板网!