稀疏矩阵转置算法（C语言）-Toy模板网

这篇具有很好参考价值的文章主要介绍了稀疏矩阵转置算法（C语言）。希望对大家有所帮助。如果存在错误或未考虑完全的地方，请大家不吝赐教，您也可以点击"举报违法"按钮提交疑问。

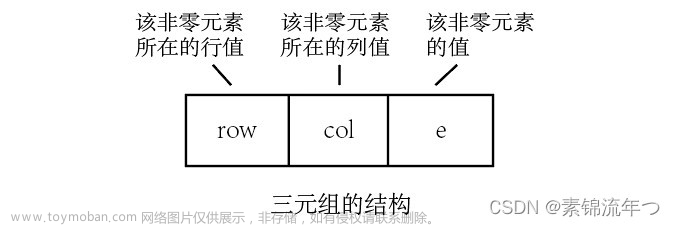
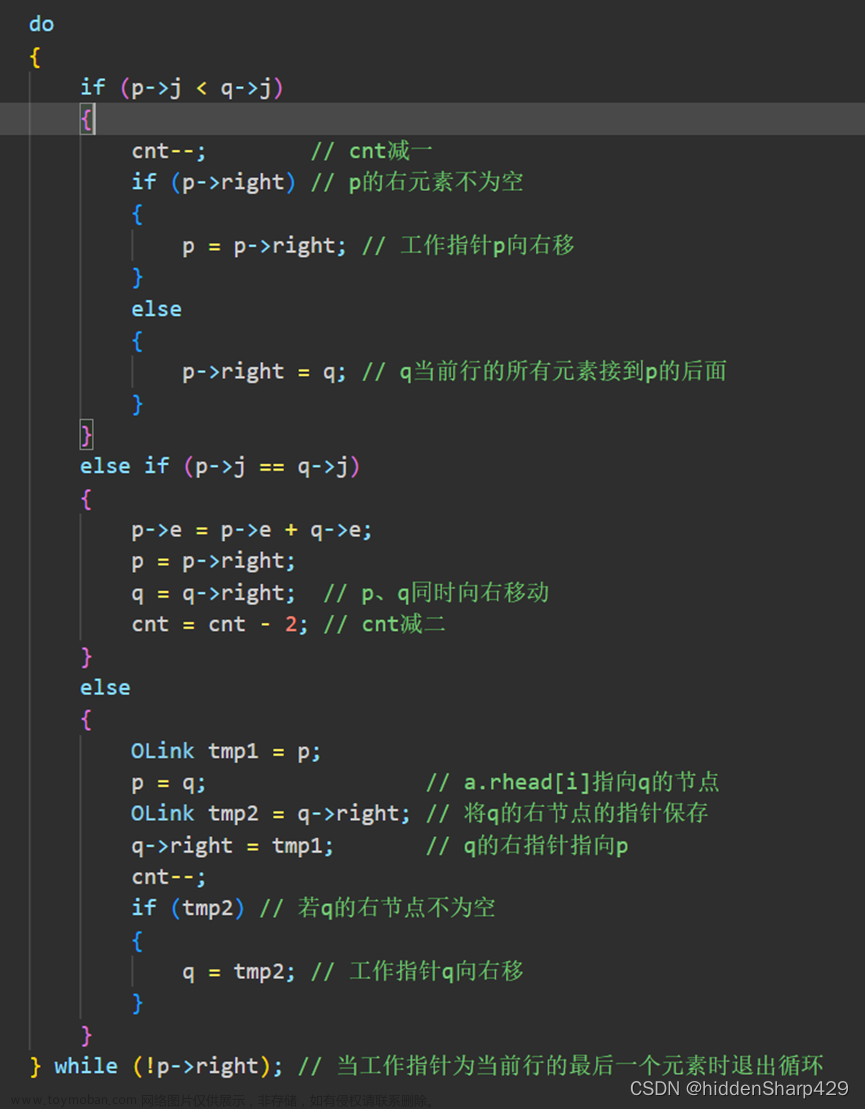
（参考数据结构教材，严蔚敏，吴伟民版 p99，多谢阅读，望对您有帮助）
无论是几维的数组，在计算机中都是以一维数组的方式进行存储的。
矩阵：相当于二维数组，它的存储，依然是用一维数组的方式进行存储。
nxn的矩阵，在计算机空间上，需要nxn个空间。
稀疏矩阵的压缩：将矩阵中的值为零或者为常数C的某c个数，不做存储（或者共用同样的空间，本题转置对0不做存储），压缩后原本nxn的矩阵，存储只需要nxn-c的空间
下面以这样的M矩阵进行转置
1 2 3
4 0 0
0 5 1
转置后得N矩阵：
1 4 0
2 0 5
3 0 1
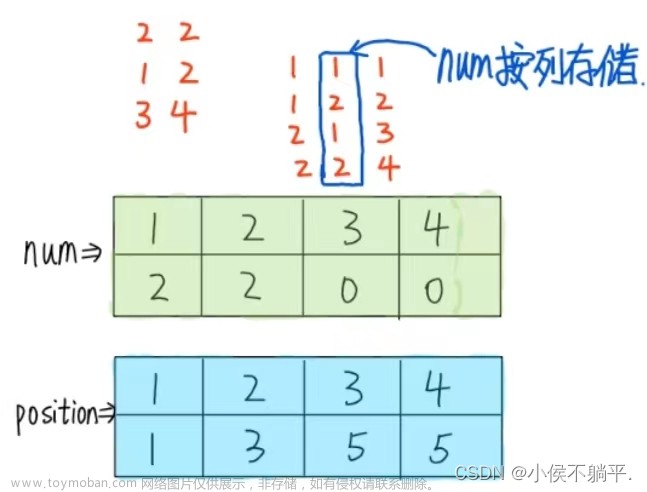
M矩阵的计算机三元组存储方式（此图为图1）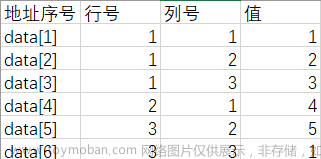
稀疏矩阵转置算法（C语言）
转置后T矩阵的计算机三元组存储方式（此图为图2）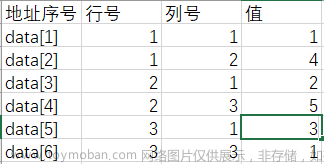

转置过程的实现，实际上是从图一转化为图二的过程
因为图1是按照行储存（第一行储存完了，才储存第二行），转置后的T矩阵，同样是按照行进行存储。
故T矩阵再遍历矩阵M时，M的列就是T的行，把M的每列的数据，逐列，一一存到data中，完成转置运算

先给出转置代码实现：

#include "stdio.h"
#include "stdlib.h"

#define Max_size 1000

typedef struct 
{
	int i;//矩阵中数据的行号
	int j;//矩阵中数据的列号
	int e;//i行j列，数据的值
}Triple;//三元组为一个节点

typedef struct
{
	Triple data[Max_size + 1];//data[0]未用
	int mu, nu, tu;//矩阵的行数，列数，非零元个数
}Matrix;

void TransposeSMatrix(Matrix M,Matrix &T)//将矩阵M转置为T
{
	T.mu = M.nu; T.nu = M.mu; T.tu = M.tu;
	if (T.tu)//非零元不为0
	{
		int q = 1;//用于逐项记录转置后矩阵T的值
		int col, p;//矩阵M的col列号，p:指向当前值在M矩阵硬件的储存位置
		for (col = 1; col < M.nu; col++)
		{
			for (p = 1; p < M.tu; p++)
			{
				if (M.data[p].j == col)//逐列进行遍历，并插入到T.data中
				{
					T.data[q].i = M.data[p].j;
					T.data[q].j = M.data[p].i;//转置后i，j互换
					T.data[q].e = M.data[p].e;//T的值获取到
					q++;//T指针的数据后移
				}
			}
		}
	}
}

int main()
{
	Matrix M,T;
	M.mu = 3;
	M.nu = 3;
	M.tu = 6;
	M.data[1].i = 1;
	M.data[1].j = 1;
	M.data[1].e = 1;

	M.data[2].i = 1;
	M.data[2].j = 2;
	M.data[2].e = 2;

	M.data[3].i = 1;
	M.data[3].j = 3;
	M.data[3].e = 3;

	M.data[4].i = 2;
	M.data[4].j = 1;
	M.data[4].e = 4;

	M.data[5].i = 3;
	M.data[5].j = 2;
	M.data[5].e = 5;

	M.data[6].i = 3;
	M.data[6].j = 3;
	M.data[6].e = 1;

	TransposeSMatrix(M, T);
	printf("(%d,%d):%d", T.data[4].i, T.data[4].j, T.data[4].e);//求转置后T矩阵2行3列的值
	return 0;
}