算法基础（二）（共有30道例题）-Toy模板网

这篇具有很好参考价值的文章主要介绍了算法基础（二）（共有30道例题）。希望对大家有所帮助。如果存在错误或未考虑完全的地方，请大家不吝赐教，您也可以点击"举报违法"按钮提交疑问。

六、数据结构

（一）数组

定义：数组是存放在连续内存空间上的相同类型数据的集合。数组可以方便的通过下标索引的方式获取到下标下对应的数据。
注意：
（1）数组下标都是从0开始的。
（2）数组内存空间的地址是连续的。正是因为数组的在内存空间的地址是连续的，所以我们在删除或者增添元素的时候，就难免要移动其他元素的地址。
（3）使用C++的话，要注意vector 和 array的区别，vector的底层实现是array，严格来讲vector是容器，不是数组。
（4）二维数组在内存的空间地址是连续的么？
答：不同编程语言的内存管理是不一样的，以C++为例，在C++中二维数组是连续分布的

1.数组之二分查找

例题1：二分查找

这道题目的前提是数组为有序数组，同时题目还强调数组中无重复元素。这是最简单的二分查找的题目。
题目难度：简单

class Solution {
public:
    int search(vector<int>& nums, int target) 
    {
        int left = 0;
        int right = nums.size() - 1;
        while (left <= right)//截至条件相当于是区间的大小 < 1
        //假如left==right，那么left==middle==right
        {
            int middle = left + ((right - left) / 2);
            if(nums[middle]>target)//说明target在middle左边
            {
                right=middle-1;
            }
            else if(nums[middle]<target)//说明target在middle右边
            {
                left=middle+1;
            }
            else return middle;//nums[middle]==target
        }
        return -1;
    }
};

例题2：数的范围

算法基础（二）（共有30道例题）
本质是：边界有一半区间满足条件，一半不满足。我们可以找到这两个区间的边界。相当于找绿色区域的左边界，找红色区域的右边界。
mid是中间的下标，x是要查找的数。

找左边界
如果mid满足绿色区域的条件（q[mid]>=x），那么从右侧逼近，right=mid，如果mid不满足绿色区域的条件，即mid在红色区域，那就从左侧逼近，left=mid+1；
找右边界
如果mid满足红色区域的条件（q[mid]<=x），那么从左侧逼近，left=mid，如果mid不满足红色区域的条件，即mid在绿色区域，那就从右侧逼近，right=mid-1；

题目

#include <iostream>
using namespace std;

const int N = 100010;
int n, m;
int q[N];

int main()
{
    cin>>n>>m;  
    for(int i=0;i<n;i++) cin>>q[i];    
    while(m--)
    {
        int x;
        cin>>x;//要查找的数
    
        int left=0,right=n-1;                
        while(left<right)
        {
            int mid = (left + right) >> 1;
            if(q[mid]>=x) right=mid;//向左逼近,找左边界  x...mid...
            else left=mid+1;//mid...x...
        }
        
        if(q[left]!=x) cout<<"-1 -1"<<endl;
        else
        {
            cout<<left<<" ";
                        
            int left = 0, right = n - 1;      
            
            while(left<right)
            {
                int mid=(left + right +1) >> 1;
                if (q[mid] <= x) left = mid;//向右逼近，找右边界
                else right = mid - 1;
            }
            cout<<right<<endl;
        }
    }        
    return 0;
}

例题3：在排序数组中查找元素的第一个和最后一个位置

题目难度：中等

class Solution {
public:  
    vector<int> res={-1,-1};
    vector<int> searchRange(vector<int>& nums, int target) 
    {
        int n=nums.size();

        if(n==0) return{-1,-1};
    
        int left=0,right=n-1;
        
        while(left<right)
        {
            int mid = (left + right) >> 1;
            if(nums[mid]>=target) right=mid;//向左逼近,找左边界  x...mid...
            else left=mid+1;//mid...x...
        }
        
        if(nums[left]!=target) return {-1,-1};
        else
        {
            res[0]=left;
            
            int left = 0, right = n - 1;
        
            while(left<right)
            {
                int mid=(left + right +1) >> 1;
                if (nums[mid] <= target) left = mid;//向右逼近，找右边界
                else right = mid - 1;
            }
            res[1]=left;
        }
        return res;
    }      
};

2.数组之移除元素

例题4：移除元素

题目难度：中等
数组的元素在内存地址中是连续的，不能单独删除数组中的某个元素，只能覆盖。
方法一：暴力

class Solution {
public:
    int removeElement(vector<int>& nums, int val) 
    {
        int len=nums.size();
        for(int i=0;i<len;i++)
        {
            if(nums[i]==val) //找到要删除的元素了
            {
                for (int j = i + 1; j < len; j++) 
                {
                    nums[j - 1] = nums[j];
                }
                i--;
                len--;
            }
        }
        return len;
    }
};

方法二：双指针
定义快慢指针
快指针：寻找新数组的元素，新数组就是不含有目标元素的数组。
慢指针：指向更新新数组下标的位置。

class Solution {
public:
    int removeElement(vector<int>& nums, int val) 
    {
        int slow_index = 0;
        //快指针：寻找新数组的元素 ，新数组就是不含有目标元素的数组
        //慢指针：指向更新 新数组下标的位置
        for(int fast_index=0;fast_index<nums.size();fast_index++)
        {
            if (val != nums[fast_index]) //如果不是要移除的元素
            {
                nums[slow_index] = nums[fast_index];
                slow_index++;
            }
        }
        return slow_index;
    }
};

（二）链表

1.链表之静态链表(用数组模拟单链表)

例题5：单链表

题目
注意:题目中第 k个插入的数并不是指当前链表的第 k 个数。例如操作过程中一共插入了 n个数，则按照插入的时间顺序，这 n 个数依次为：第 1 个插入的数，第 2 个插入的数，…第 n 个插入的数。

#include<iostream>
using namespace std;

const int N=1e6+10;
// head存储链表头(表示头节点的下标)，e[i]存储节点i的值，ne[i]存储节点i的next指针，idx表示当前用到了哪个节点(相当于指针)
int head, e[N], ne[N], idx;

// 初始化:链表是空的：head->空，空节点的下标用-1来表示
void init()
{
    head = -1;
    idx = 0;
}
//在表头插入一个数a
void add_to_head(int a)
{
    e[idx] = a;
    ne[idx] = head;//(1)插入的节点的next指针指向了原本head指向数据
    head=idx;//(2)原本的head指向了插入元素a；
    idx++;
}

//题目中第k个插入的数并不是指当前链表的第k个数。
//例如操作过程中一共插入了n个数，则按照插入的时间顺序，这n个数依次为：第1个插入的数，第2个插入的数，…第 n个插入的数。

//将数据x插入到下标是k的节点后面
void add_to_k(int k,int x)
{
    e[idx]=x;
    ne[idx]=ne[k];
    ne[k]=idx;
    idx++;
}
//将第k个的节点后面的一个节点删掉
void remove(int k)
{
    ne[k]=ne[ne[k]];
}

int main()
{
    int m;//操作次数
    cin>>m;    
    init();//初始化    
    while(m--)
    {
        char s;
        int k;
        int x;
    
        cin>>s;
        if(s=='H')
        {
            cin>>x;
            add_to_head(x);
        }
        else if(s=='I')
        {
            cin>>k>>x;
            add_to_k(k-1,x);
        }
        else 
        {
            cin>>k;
            if(!k) head=ne[head];//当k为0时，表示删除头结点。
            //举例：1，2，3，4。k=0时，删除1即可，即head指向2，2的下标为ne[head];   
            remove(k-1);
        }
    }    
    for(int i=head;i!=-1;i=ne[i])
    {
        cout<<e[i]<<' ';
    }
    cout<<endl; 
    return 0;
}

2.链表之静态链表（用数组模拟双链表）

例题6：双链表

题目

#include<iostream>
using namespace std;
#include<string>

const int N=1e6+10;

//e[]表示节点的值，l[]表示节点的左指针，r[]表示节点的右指针，idx表示当前用到了哪个节点
int e[N], l[N], r[N], idx;

//struct Node{
    //int e,l,r;
//}nodes[N];

// 初始化
void init()
{
    //0是左端点(head)，1是右端点(tail)
    r[0] = 1, l[1] = 0;
    idx = 2;//因为0和1已经被占用了
}
//表示在第 k 个插入的数右侧插入一个数x。
void add(int k,int x)
{
    e[idx]=x;
    r[idx]=r[k];
    l[idx]=k;
    
    l[r[k]]=idx;//r[k]是第k个插入节点的右边节点的idx
    r[k]=idx;
    
    idx++;
}
//在第 k 个插入的数左侧插入一个数x：其实就是在第l[k]个数右边插入一个数x
//add(l[k],x)

//表示将第 k 个插入的数删除，第 k 个数左边的数的下标l[k],第 k 个数右边的数的下标r[k]
void remove(int k)
{
    r[l[k]]=r[k];
    l[r[k]]=l[k];
    
    //nodes[nodes[k].l].r=nodes[k].r;
}

int main()
{
    int m;//操作次数
    cin>>m;
    init();
    while(m--)
    {
        string s;
        cin>>s;
        int k;
        int x;
        if(s=="L")//表示在链表的最左端插入数x，即在head的右边插入x
        {
            cin>>x;
            add(0,x);
        }
        else if(s=="R")//表示在链表的最右端插入数x，即在tail的左边插入x
        {
            cin>>x;
            add(l[1],x);
        }
        else if(s=="D")
        {
            cin>>k;
            remove(k+1);
        }
        else if(s=="IR")
        {
            cin>>k>>x;
            add(k+1,x);
        }
        else
        {
            cin>>k>>x;
            add(l[k+1],x);
        }
    }
    for(int i=r[0];i!=1;i=r[i]) cout<<e[i]<<' ';
    cout<<endl;
    return 0;
}

3.链表之删除元素

例题7：移除链表元素：给你一个链表的头节点 head 和一个整数 val ，请你删除链表中所有满足 Node.val == val 的节点，并返回新的头节点。

题目难度：简单
在这道题里头结点（题目中也给出了定义：ListNode* head）的val是有正常数字的，不是摆设，所以我们可以设一个虚拟头结点放在原来头结点前面。

/**
 * Definition for singly-linked list.
 * struct ListNode {
 *     int val;
 *     ListNode *next;
 *     ListNode() : val(0), next(nullptr) {}
 *     ListNode(int x) : val(x), next(nullptr) {}
 *     ListNode(int x, ListNode *next) : val(x), next(next) {}
 * };
 */
class Solution {
public:
    ListNode* removeElements(ListNode* head, int val) 
    {
        ListNode* dummy_head=new ListNode(0);//设置虚拟头结点
        dummy_head->next=head;//设置虚拟头节点；放在head前面
        ListNode *cur=dummy_head;
        while(cur->next!=nullptr)
        {
            if(cur->next->val==val)
            {
                ListNode *node_delete=cur->next;
                ListNode *tmp=cur->next->next;
                //cur是要删除结点的上一个结点的指针，cur->next->next是要删除结点的下一个结点指针
                cur->next=tmp;
                delete node_delete;
            }
            else
            {
                cur=cur->next;
            }
        }
        head=dummy_head->next;//先保存新的头结点
        delete dummy_head;
        return head;
    }
};

昨晚在力扣上面提交代码不停出错，原因是最后三行我原本写的是：

delete dummy_head;
return dummy_head->next;

已经删去了虚拟头结点，怎么可以再返回虚拟头结点的next呢？

例题8：删除排序链表中的重复元素给定一个已排序的链表的头 head ，删除所有重复的元素，使每个元素只出现一次。返回已排序的链表。

题目难度：简单

/**
 * Definition for singly-linked list.
 * struct ListNode {
 *     int val;
 *     ListNode *next;
 *     ListNode() : val(0), next(nullptr) {}
 *     ListNode(int x) : val(x), next(nullptr) {}
 *     ListNode(int x, ListNode *next) : val(x), next(next) {}
 * };
 */
class Solution {
public:
    ListNode* deleteDuplicates(ListNode* head) 
    {
        if (head == nullptr)
	    {
		    return head;
	    }
	    
        ListNode* fast=head->next;
        ListNode* slow=head;

        while(fast!=nullptr)
        {
            if(fast->val==slow->val)
            {
                //ListNode *tmp=fast->next;
                ListNode* node_delete=fast;
                fast=fast->next;
                slow->next=fast;
                
                delete node_delete;
            }
            else
            {
                fast=fast->next;
                slow=slow->next;
            }
        }
  
        return head;
    }
};

在力扣提交了好几次都错误的原因：没有写下面这段话

if (head == nullptr)
{
	return head;
}

没有想到如果链表为空怎么办

例题9：删除链表的倒数第N个结点：给你一个链表，删除链表的倒数第 n 个结点，并且返回链表的头结点。

题目难度：中等
这道题用到了双指针：fast和slow，fast从虚拟头结点开始跑N+1个，再让slow和fast一起跑，直到fast跑到NULL,这样slow就跑到了要删除的结点的前一个结点；

/**
 * Definition for singly-linked list.
 * struct ListNode {
 *     int val;
 *     ListNode *next;
 *     ListNode() : val(0), next(nullptr) {}
 *     ListNode(int x) : val(x), next(nullptr) {}
 *     ListNode(int x, ListNode *next) : val(x), next(next) {}
 * };
 */
class Solution {
public:
    ListNode* removeNthFromEnd(ListNode* head, int n) 
    {
        ListNode *dummy_head=new ListNode(0);
        dummy_head->next=head;
        ListNode* fast=dummy_head;
        ListNode* slow=dummy_head;
        for(int i=0;i<n+1;i++)
        {
            fast=fast->next;//fast先走n+1步

        }
        while(fast!=nullptr)
        {
            fast=fast->next;
            slow=slow->next;
        }
        ListNode* temp=slow->next->next;//这是要删除的结点的下一个结点的指针
        ListNode* node_delete=slow->next;
        slow->next=temp;
        
        head=dummy_head->next;
        delete dummy_head;
        delete node_delete;
        return head;
    }
};

2.链表之交换结点：

例题10：两两交换链表中的节点：给你一个链表，两两交换其中相邻的节点，并返回交换后链表的头节点。你必须在不修改节点内部的值的情况下完成本题（即，只能进行节点交换）。

题目难度：中等

/**
 * Definition for singly-linked list.
 * struct ListNode {
 *     int val;
 *     ListNode *next;
 *     ListNode() : val(0), next(nullptr) {}
 *     ListNode(int x) : val(x), next(nullptr) {}
 *     ListNode(int x, ListNode *next) : val(x), next(next) {}
 * };
 */
class Solution {
public:
    ListNode* swapPairs(ListNode* head) 
    {
        if(head==nullptr)
        {
            return head;
        }
        ListNode* dummy_head=new ListNode(0);
        dummy_head->next=head;
        ListNode *p=dummy_head;
        while(p->next != nullptr&&p->next->next!=nullptr)
        {
            ListNode* fast=p->next->next;
            ListNode* slow=p->next;
            ListNode *tmp=fast->next;

            p->next=fast;
            fast->next=slow;
            slow->next = tmp;

            p=p->next->next;
        }
        head=dummy_head->next;
        delete dummy_head;
        return head;
    }
};

在力扣提交了好几次都错误的原因：

while(p->next != nullptr&&p->next->next!=nullptr)

我写成了：

while(p->next != nullptr)

没有想到如果链表里的元素的个数是奇数怎么办

3.链表之反转：

例题11：反转链表：给你单链表的头节点 head ，请你反转链表，并返回反转后的链表。

题目

/**
 * Definition for singly-linked list.
 * struct ListNode {
 *     int val;
 *     ListNode *next;
 *     ListNode() : val(0), next(nullptr) {}
 *     ListNode(int x) : val(x), next(nullptr) {}
 *     ListNode(int x, ListNode *next) : val(x), next(next) {}
 * };
 */
class Solution {
public:
    ListNode* reverseList(ListNode* head) 
    {
        if(head==nullptr)
        {
            return head;
        }
        dummy_head->next=head;
        ListNode *pre=nullptr;
        ListNode *cur=head;
        while(cur!=nullptr)
        {
            ListNode* tmp=cur->next;//保存cur的下一个结点
            cur->next=pre;
            pre=cur;
            cur=tmp;//tmp=cur->next

        }
        
        return pre;
    }
};

在力扣提交了好几次都错误的原因：

ListNode *pre=nullptr;

而我把pre指针指向了一个虚拟头结点（0，nullptr），里面是有数值0的

（三）栈

1.用数组模拟栈

例题12：模拟栈

题目

#include<iostream>
using namespace std;

const int N=1e6+10;
int idx=0;
int stack[N];//数组模拟栈

//向栈顶插入一个数 x
void push(int x)
{
    stack[++idx]=x;
}

//从栈顶弹出一个数
void pop()
{
    idx--;
}

//判断栈是否为空
bool empty()
{
    if(idx==0) return true;//空的
    else if(idx>0) return false;
}

//查询栈顶元素
void query()
{
    cout<<stack[idx]<<endl;
}

int main()
{
    int m;//操作次数
    cin>>m;
    
    string s;
    int x;
    
    while(m--)
    {
        cin>>s;
        if(s=="push")
        {
            cin>>x;
            push(x);
        }
        else if(s=="query")
        {
            query();
        }
        else if(s=="pop")
        {
            pop();
        }
        else if(s=="empty")
        {
            bool flag=empty();
            if(flag==1) cout<<"YES"<<endl;
            else cout<<"NO"<<endl;
        }
    }
    return 0;
}

2.栈之单调栈

常见模型：找出每个数左边离它最近的比它大/小的数
算法基础（二）（共有30道例题）

int tt = 0;
for (int i = 1; i <= n; i ++ )
{
    while (tt && check(stk[tt], i)) tt -- ;
    stk[ ++ tt] = i;
}

例题13：单调栈

题目难度：简单
方法一：暴力（不推荐）时间复杂度 $O（n^2）$ 。

#include<iostream>
using namespace std;

const int N=1e5+10;
int arr[N];
int res[N];

int main()
{
    int n;
    cin>>n;
    
    for(int i=0;i<n;i++)
    {
        cin>>arr[i];
    }
    
    //先将res全部赋值-1
    for(int i=0;i<n;i++)
    {
        res[i]=-1;
    }
    
    for(int i=1;i<n;i++)
    {
        for(int j=i-1;j>=0;j--)
        {
            if(arr[j]<arr[i]) 
            {
                res[i]=arr[j];
                break;
            }
        }
    }
    
    for(int i=0;i<n;i++) cout<<res[i]<<" ";
    cout<<endl;
}

方法二：单调栈，时间复杂度 $O （ n ）$ 。
这道题其实使用scanf和printf速度会变快。

#include<iostream>
using namespace std;

const int N=1e5+10;
int n;
int stk[N],tt=0;

int main()
{
    cin.tie(0);
    ios::sync_with_stdio(false);
    cin>>n;    
    for(int i=0;i<n;i++)
    {
        int x;
        cin>>x;
        while(tt!=0&&stk[tt]>=x) tt--;
        if(tt!=0) cout<<stk[tt]<<' ';
        else cout<<-1<<' ';
        
        stk[++tt]=x;
    }
    return 0;
}

3.栈与队列的关系

例题14：用栈实现队列

题目

class MyQueue 
{
public:
    stack<int>stack_in;
    stack<int>stack_out;

    MyQueue() 
    {

    }
    
    void push(int x) 
    {
        stack_in.push(x);
    }
    
    int pop()
    {
        if(stack_out.empty())//空的就是true
        {
            while(!stack_in.empty())
            {
                stack_out.push(stack_in.top());
                stack_in.pop();
            }
        }
        int result = stack_out.top();
        stack_out.pop();
        return result;
    }
    int peek() 
    {
        if(stack_out.empty())//空的就是true
        {
            while(!stack_in.empty())
            {
                stack_out.push(stack_in.top());
                stack_in.pop();
            }
        }
        int result=stack_out.top();
        return result;
    }
    
    bool empty() 
    {
        if (stack_in.empty()&&stack_out.empty())
        {
            return true;
        }
        else
        {
            return false;
        }
    }
};

/**
 * Your MyQueue object will be instantiated and called as such:
 * MyQueue* obj = new MyQueue();
 * obj->push(x);
 * int param_2 = obj->pop();
 * int param_3 = obj->peek();
 * bool param_4 = obj->empty();
 */

例题15：用两个队列实现栈

题目

class MyStack {
public:
    queue<int> queue1;//这是用来模仿栈的
    queue<int> queue2;
    MyStack() {

    }
    
    void push(int x) 
    {
        queue1.push(x);
    }
    
    int pop() 
    {
        int size=queue1.size();
        size--;
        while(size--)
        {
            queue2.push(queue1.front());
            queue1.pop();//从头部弹出元素
        }
        int result=queue1.back();
            
        queue1.pop();
        queue1=queue2;
        while (!queue2.empty()) 
        { // 清空queue_out
            queue2.pop();
        }
       
        return result;
    }
    
    int top() 
    {
        int result=queue1.back();
        return result;
    }
    
    bool empty() 
    {
        if(queue1.empty())
        {
            return true;
        }
        else
        {
            return false;
        }
    }
};

/**
 * Your MyStack object will be instantiated and called as such:
 * MyStack* obj = new MyStack();
 * obj->push(x);
 * int param_2 = obj->pop();
 * int param_3 = obj->top();
 * bool param_4 = obj->empty();
 */

补充：用一个队列实现栈

class MyStack 
{
public:
    queue<int> que;
    /** Initialize your data structure here. */
    MyStack() {

    }
    /** Push element x onto stack. */
    void push(int x) 
    {
        que.push(x);
    }
    /** Removes the element on top of the stack and returns that element. */
    int pop() 
    {
        int size = que.size();
        size--;
        while (size--) 
        { // 将队列头部的元素（除了最后一个元素外） 重新添加到队列尾部
            que.push(que.front());
            que.pop();
        }
        int result = que.front(); // 此时弹出的元素就是栈的顶部
        que.pop();
        return result;
    }

    /** Get the top element. */
    int top() 
    {
        return que.back();
    }

    /** Returns whether the stack is empty. */
    bool empty() 
    {
        return que.empty();
    }

4.栈与匹配

例题16：有效的括号(此题想了很久，最后看了答案)

题目难度：简单
解题思路:

先判断字符串大小是否是2的倍数,不是2的倍数一定匹配不上!
遍历字符串:
第一种情况：已经遍历完了字符串，但是栈不为空，说明有相应的左括号没有右括号来匹配，所以return false
第二种情况：遍历字符串匹配的过程中，发现栈里没有要匹配的字符。所以return false
第三种情况：遍历字符串匹配的过程中，栈已经为空了，没有匹配的字符了，说明右括号没有找到对应的左括号return false
最后判断栈是否为空,空的栈括号能匹配上,不是空的栈匹配不上!

class Solution 
{
public:
    stack<char> s1;
    bool isValid(string s) 
    {
        int size=s.length();
        if(size%2!=0)
        {
            return false;
        }
        //if(size==0) return true;
        for(int i=0;i<size;i++)
        {
            if(s[i]=='(')
            {
                s1.push(')');
            }
            else if(s[i]=='{')
            {
                s1.push('}');
            }
            else if(s[i]=='[')
            {
                s1.push(']');
            }
            else if (s1.empty() || s1.top() != s[i]) //第三种和第二种
            {
            	return false;
            }
            else if(s1.top()==s[i]) s1.pop();// st.top() 与 s[i]相等，栈弹出元素
        }
		 // 第一种情况：此时我们已经遍历完了字符串，但是栈不为空，说明有相应的左括号没有右括号来匹配，所以return false，否则就return true
        return s1.empty();

    }
};

例题17：删除字符串中的所有相邻重复项

题目难度：简单

class Solution {
public:
    stack<char> sta;

    string removeDuplicates(string s) 
    {
        string s_new;
        int size=s.length();
        for(int i=0;i<size;i++)
        {
            if(sta.empty() || s[i]!= sta.top())
            {
                sta.push(s[i]);
            }
            else
            {
                sta.pop();
            }
        }
        
        while(!sta.empty())
        {
            s_new+=sta.top();
            sta.pop();
        }
        reverse(s_new.begin(), s_new.end()); 
        return s_new;
    }
};

总结：

字符串拼接：
（1）+
（2） apeend
字符串反转：

string s;
reverse(s.begin(), s.end());

5.栈之逆波兰

例题18：逆波兰表达式求值（输入直接就是后缀表达式）

什么是后缀表达式：2，1，+，3，*
什么是中缀表达式：（2+1）*3
题目难度：中等
算法基础（二）（共有30道例题）
规则：从左往右遍历这个表达式的每个数字和符号，凡是遇到数字就进sta栈，遇到符号，就将栈顶的两个数字出栈，进行运算，再将运算结果进sta栈。

class Solution 
{
public:
    int evalRPN(vector<string>& tokens) 
    {
        int size=tokens.size();
       
        stack<int> sta;
        for(int i=0;i<size;i++)
        {
            if((tokens[i]!="+")&&(tokens[i]!="-")&&(tokens[i]!="*")&&(tokens[i]!="/"))
            {
                sta.push(stoi(tokens[i]));
            }
            else if(tokens[i]=="+")
            {
                int a=sta.top();
                sta.pop();
                int b=sta.top();
                sta.pop();
                sta.push(a+b);
            }
            else if(tokens[i]=="-")
            {
                int a=sta.top();
                sta.pop();
                int b=sta.top();
                sta.pop();
                sta.push(b-a);
            }
            else if(tokens[i]=="*")
            {
                int a=sta.top();
                sta.pop();
                int b=sta.top();
                sta.pop();
                sta.push(a*b);
            }
            else if(tokens[i]=="/")
            {
                int a=sta.top();
                sta.pop();
                int b=sta.top();
                sta.pop();
                sta.push(b/a);
            }
        }
        int result=sta.top();
        return result;
    }
};

总结：
（1）字符串与数字之间的转换：

//1.字符串转成数字
stod()//字符串转double
stof()//字符串转float
stoi()//字符串转int
stol()//字符串转long
stold()//字符串转double
stoll()//字符串转long long
//2.字符转换成数字
atoi()
//2.数字转成字符串
string to_string(待转换的数字)

stoi()与atoi()不同点：
①atoi()的参数是 const char* ,因此对于一个字符串str我们必须调用 c_str()的方法把这个string转换成 const char类型的,而stoi()的参数是const string,不需要转化为 const char*；
②stoi()会做范围检查，默认范围是在int的范围内的，如果超出范围的话则会runtime error！而atoi()不会做范围检查，如果超出范围的话，超出上界，则输出上界，超出下界，则输出下界；
（2）字符与数字之间的转换

char转换为int类型：
char类型的变量减去一个'0'；
例如：
char b ='5';
int a=b-'0'

总结：

stoi用来转化string的，atoi转化的是char[].
char[]转string可以直接赋值或者用一个循环
string转char：
str.c_str()
个人感觉stoi的能力还是要比atoi的能力要大一些的，stoi可能往往要比atoi要好用。

例题19：表达式求值（输入是中缀表达式）

int isdigit(int c);
参数：c – 这是要检查的字符。
返回值：如果 c 是一个数字，则该函数返回非零值，否则返回 0。
C 库函数 int isdigit(int c) 检查所传的字符是否是十进制数字字符。
十进制数字是：0 1 2 3 4 5 6 7 8 9

#include <iostream>
#include <cstring>
#include <algorithm>
#include <stack>
#include <unordered_map>

using namespace std;

stack<int> num;//存放数字
stack<char> op;//存放符号

void eval()
{
    auto b = num.top(); num.pop();
    auto a = num.top(); num.pop();
    auto c = op.top(); op.pop();
    int x;
    if (c == '+') x = a + b;
    else if (c == '-') x = a - b;
    else if (c == '*') x = a * b;
    else x = a / b;
    num.push(x);
}

int main()
{
    unordered_map<char, int> pr{{'+', 1}, {'-', 1}, {'*', 2}, {'/', 2}};//乘除的等级更高点
    string str;
    cin >> str;
    for (int i = 0; i < str.size(); i ++ )
    {
        auto c = str[i];
        if (isdigit(c))//(2+2)*(1+1)  i=1时是数字
        {
            int x = 0, j = i;
            while (j < str.size() && isdigit(str[j]))//靠这个while循环将连续的数字放入到num中
            {
                x =  10*x+str[j] - '0';//为何要10*x：比如(23+4)*(1+1)，输入23一定要10*2+3
                j++;
                
            }
            i = j - 1;//因为上面j++
            num.push(x);
        }
        
        else if (c == '(') op.push(c);//存放'('
        else if (c == ')')
        {
            while (op.top() != '(') eval();//从右往左eval一下，直到遇到（
            op.pop();
        }
        else
        {
            while (op.size() && op.top() != '(' && pr[op.top()] >= pr[c]) eval();//pr[+]=pr[-]=1
            op.push(c);
        }
    }
    while (op.size()) eval();
    cout << num.top() << endl;
    return 0;
}

（四）队列

1.用数组模拟队列

例题19：模拟队列

题目

#include<iostream>
using namespace std;

//队尾插入，队头弹出
const int N=1e6+10;
int hh=0;//队头
int tt=-1;//队尾
int query[N];//数组模拟队列

//向队尾插入一个数 x
void push(int x)
{
    query[++tt]=x;
}

//从队头弹出一个数
void pop()
{
    hh++;
}

//判断队列是否为空
bool empty()
{
    if(hh<=tt) return false;//不是空的，比如插入一个元素：tt=0,再弹出一个元素：hh=1;
    else return true;
}

//查询队头元素
void check_query()
{
    cout<<query[hh]<<endl;
}

int main()
{
    int m;//操作次数
    cin>>m;
    
    string s;
    int x;
    
    while(m--)
    {
        cin>>s;
        if(s=="push")
        {
            cin>>x;
            push(x);
        }
        else if(s=="query")
        {
            check_query();
        }
        else if(s=="pop")
        {
            pop();
        }
        else if(s=="empty")
        {
            bool flag=empty();
            if(flag==1) cout<<"YES"<<endl;
            else cout<<"NO"<<endl;
        }
    }
    return 0;
}

2.队列之单调队列

单调队列：顾名思义其中所有的元素都是单调的（递增或者递减），承载的技术数据结构是队列，实现是双端队列，队头元素为窗口的最大最小元素。
队头删除不符合有效窗口的元素，队尾删除不符合最值的候选元素。
但是单调队列不是真正的队列，因为队列都是先进先出，而单调队列不符合FIFO。
删头操作：队头元素出队列。
去尾操作：队尾元素出队列，待新元素从队尾入队，从队尾开始删除影响队列单调性的元素。
但是要保证：插入必须在去尾之后来。也就是去掉尾部不符合单调性的元素后才能插入新元素。

例题20：滑动窗口

题目难度：简单
举例：比如1进来了没事，3再进来也没事，留下1，3。但是当-1进来时，1和3都要先删掉，再只留-1 。然后-3进来，只留-3。5进来留下，留下-3，5。当3进来时，删掉5，留下-3和3。6进来，此时i=6，i-k+1=4，队头是-3，他的下标q[hh]=3，所以此时滑动窗口，-3已经出了窗口，留下3，6。7进来，留下3，6，7

#include<iostream>
using namespace std;

const int N=1e6+10;
int n,k;//n，k分别代表数组长度和滑动窗口的长度
int a[N],q[N];//q[N]里面默认是0

int main()
{
 	cin>>n>>k;
    int hh=0,tt=-1;
    for(int i=0;i<n;i++) cin>>a[i];  
    for(int i=0;i<n;i++)
    {
        if(hh<=tt&&i-k+1>q[hh]) hh++;//i-k+1是新起点，i-k+1>q[hh]说明hh已经出了窗口了        
        while(hh<=tt&&a[i]<=a[q[tt]]) tt--;//a[i]是新进来数，a[q[tt]]是队尾的数
        //比如1进来了没事，3再进来也没事，留下1，3。但是当-1进来时，1和3都要先删掉，再只留-1 q[++tt]=i。
        //然后-3进来，只留-3。5进来留下，留下-3，5。当3进来时，删掉5，留下-3和3。
        //6进来，此时i=6，i-k+1=4，队头是-3，他的下标q[hh]=3，所以此时滑动窗口，-3已经出了窗口，留下3，6。
        //7进来，留下3，6，7
        q[++tt]=i;//会发现从i=0开始，q[0]=0;q[1]=1;q[2]=2;      
        if(i>=k-1) cout<<a[q[hh]]<<" ";//从第k个数开始才有输出
        //for(int j=hh;j<=tt;j++) cout<<a[q[j]];
    }
    puts("");//换行
    hh=0,tt=-1;
    for(int i=0;i<n;i++)
    {
        if(hh<=tt&&i-k+1>q[hh]) hh++;//i-k+1是新起点，i-k+1>q[hh]说明hh已经出了窗口了        
        while(hh<=tt&&a[i]>=a[q[tt]]) tt--;
        q[++tt]=i;//会发现从i=0开始，q[0]=0;q[1]=1;q[2]=2;       
        if(i>=k-1) cout<<a[q[hh]]<<" ";//从第k个数开始才有输出      
        //for(int j=hh;j<=tt;j++) cout<<a[q[j]];
    }
    return 0;
}

例题21：滑动窗口最大值

题目难度：困难

class MyQueue {
public:
    void pop(int value) {
    }
    void push(int value) {
    }
    int front() {
        return que.front();
    }
};

设计单调队列的时候，pop，和push操作要保持如下规则：

push(value)：如果push的元素value大于队列尾部元素的数值，那么就将队列尾部的元素弹出，直到push元素的数值小于等于队列尾部元素的数值为止。
pop(value)：如果窗口移除的元素value等于单调队列头部元素，那么队列弹出元素，否则不用任何操作。
que.front()就可以返回当前窗口的最大值。

class Solution {
public:

    class MyQueue 
    {
public:

        deque<int> que; // 使用deque来实现单调队列
        //去尾
        void push(int value) 
        {
            while(!que.empty()&&value>que.back())
            {
                que.pop_back();//队尾删除不符合最值的候选元素
            }
            que.push_back(value);//插入必须在去尾后面
        }
        //删头
        void pop(int value) 
        {
            if(!que.empty()&&value==que.front())
                {
                    que.pop_front();//队头删除不符合有效窗口的元素
                }
        }
        int front() 
        {
            return que.front();
        }
};
    vector<int> maxSlidingWindow(vector<int>& nums, int k) 
    {
        vector<int> max_value;
        MyQueue myque;
        for (int i = 0; i < k; i++)  // 先将前k的元素放进队列
        {
            myque.push(nums[i]);
        }
        max_value.push_back(myque.front());
        for(int i=k;i<nums.size();i++)
        {
            myque.pop(nums[i-k]);
            myque.push(nums[i]);
            
            int max=myque.front();
            max_value.push_back(max);
        }
        return max_value;
    }
};

3.队列之优先队列

什么是优先级队列呢？
其实就是一个披着队列外衣的堆，因为优先级队列对外接口只是从队头取元素，从队尾添加元素，再无其他取元素的方式，看起来就是一个队列。
而且优先级队列内部元素是自动依照元素的权值排列。那么它是如何有序排列的呢？
缺省情况下priority_queue利用max-heap（大顶堆）完成对元素的排序，这个大顶堆是以vector为表现形式的complete binary tree（完全二叉树）。

例题22：前 K 个高频元素

题目难度：简单

priority_queue<Type, Container, Functional>
Type 为数据类型， Container 为保存数据的容器，Functional 为元素比较方式。
如果不写后两个参数，那么容器默认用的是 vector，比较方式默认用 operator<，也就是优先队列是大顶堆(less)，队头元素最大，本题为小顶堆(greater)。
emplace、emplace_front、emplace_back分别对应insert、push_front和push_back。

class KthLargest {
public:
    int K;
    priority_queue<int,vector<int>,greater<int>> que;//小顶堆：从小到大
    KthLargest(int k, vector<int>& nums) 
    {
        K=k;
        
        int size=nums.size();
        for(int i=0;i<size;i++)
        {
            que.push(nums[i]);//将nums里面的元素进行从小到大排序
        }
        for(int j=0;j<(size-k);j++)//nums里面的元素只剩k个
        {
            que.pop();
        }
    }

    int add(int val) 
    {
        
        que.push(val);
        int size_new=que.size();
        for(int j=0;j<(size_new-K);j++)
        {
            que.pop();
        }
        return que.top();

    }
};

（五）串

1.反转字符串

例题23：反转字符串

反转字符串：

reverse(str.begin(), str.end());

反转数组：

int a[5] = {1, 2, 3, 4, 5};
reverse(a, a+5);//n为数组中的元素个数

这题的本意当然是不用库函数，怎么做：双指针思想

class Solution {
public:
    void reverseString(vector<char>& s) 
    {
        int length=s.size();
        for(int i=0,j=length-1;i<length/2;i++,j--)
        {
            swap(s[i],s[j]);
        }
    }
};

总结：

字符串的长度：s.length();
字符数组的长度：s.size();
利用string头文件中的strlen()函数：strlen(str)
C++的strlen(str)和str.length()和str.size()都可以求字符串长度。其中str.length()和str.size()是用于求string类对象的成员函数，strlen(str)是用于求字符数组的长度，其参数是char*。
这题里面的str是放在了vector字符数组里面，所以用size();

例题24：反转字符串 II

难度：简单

class Solution {
public:
    string reverseStr(string s, int k) 
    {
        int length=s.length();
        
        for(int j=0;j<length;j+=(2*k))//j=0,2k,4k....      
        {
            if(length-j<k)//如果剩余字符少于 k 个，则将剩余字符全部反转。
            {
                reverse(s.begin()+j,s.end());
            }
            else if((length-j<2*k)&&(length-j>=k))
            //如果剩余字符小于 2k 但大于或等于 k 个，则反转前 k 个字符，其余字符保持原样。
            {
                reverse(s.begin()+j,s.begin()+j+k);
            }
            else 
            {
                reverse(s.begin()+j,s.begin()+j+k);
            }
        }
        return s;
    }
};

总结：

begin
解释：begin()函数返回一个迭代器,指向字符串的第一个元素.
end
解释：end()函数返回一个迭代器，指向字符串的末尾(最后一个字符的下一个位置).

2.字符串之双指针

例题25：剑指 Offer 05 替换空格：请实现一个函数，把字符串 s 中的每个空格替换成"%20"。

方法一：replace
找有多少个空格，在有空格的位置用replace

class Solution {
public:
    string replaceSpace(string s) 
    {  
        for (int i = 0; i < s.length(); i++) 
        {
            if (s[i] == ' ') 
            {
                s.replace(i, 1, "%20");
            }
        }
        return s;
    }
};

方法二：双指针
首先扩充数组到每个空格替换成"%20"之后的大小。然后从后向前替换空格，也就是双指针法，j指向新长度的末尾，i指向旧长度的末尾。
问题：从前向后填充不行么？
从前向后填充就是O(n^2)的算法了，因为每次添加元素都要将添加元素之后的所有元素向后移动。其实很多数组填充类的问题，都可以先预先给数组扩容带填充后的大小，然后在从后向前进行操作。
这么做有两个好处：
（1）不用申请新数组。
（2）从后向前填充元素，避免了从前向后填充元素时，每次添加元素都要将添加元素之后的所有元素向后移动的问题。

class Solution {
public:
    string replaceSpace(string s) 
    {  
        int size=s.length();
        int count=0;
        for(int i=0;i<s.length();i++)
        {
            if(s[i]==' ')
            {
                count++;//有多少空格
            }
        }
        
        s.resize(2*count+size,' ');//扩充
        int size_new=s.length();
      
        for(int i=size-1,j=size_new-1;i<j;i--,j--)//j是新字符串的尾端
        {
            if(s[i]!=' ')
            {
                s[j]=s[i];
            }
            else
            {
                s[j]='0';
                s[j-1]='2';
                s[j-2]='%';
                j=j-2;
            }            
        }
        return s;
    }
};

3.字符串之匹配KMP算法

举个例子：要在文本串：aabaabaafa 中查找是否出现过一个模式串：aabaaf。

先在模式串里面找连续子串。
前缀是指不包含最后一个字符的所有以第一个字符开头的连续子串。
后缀是指不包含第一个字符的所有以最后一个字符结尾的连续子串。
在这些子串里面找最长相等前后缀。
得到前缀表（前缀表里面放的是最长相等前后缀的长度），前缀表是用来回退的，它记录了模式串与主串(文本串)不匹配的时候，模式串应该从哪里开始重新匹配。

子串	最长相同前后缀的长度
a	0
aa	1
aab	0
aaba	1
aabaa	2
aabaaf	0

找到的不匹配的位置，那么此时我们要看它的前一个字符的前缀表的数值是多少。
比如aabaaf里面不匹配的位置是f，他前一个字符的前缀表的数值是2，所以把下标移动到文本串下标2的位置继续比配。
最后就在文本串中找到了和模式串匹配的子串了

代码：

先构造next数组：
（1）初始化：定义两个指针i和j，j指向前缀末尾位置，i指向后缀末尾位置。next[i] 表示 i（包括i）之前最长相等的前后缀长度（其实就是j），所以next[0] = j;

int j = -1;
next[0] = j;

（2）处理前后缀不相同的情况：如果 s[i] 与 s[j+1]不相同，也就是遇到前后缀末尾不相同的情况，就要向前回退。
怎么回退呢？next[j]就是记录着j（包括j）之前的子串的相同前后缀的长度。那么 s[i] 与 s[j+1] 不相同，就要找 j+1前一个元素在next数组里的值（就是next[j]）。
（3）处理前后缀相同的情况：如果 s[i] 与 s[j + 1] 相同，那么就同时向后移动i 和j 说明找到了相同的前后缀，同时还要将j（前缀的长度）赋给next[i], 因为next[i]要记录相同前后缀的长度。

void getNext(int* next, const string& s) {
        int j = 0;
        next[0] = 0;
        for(int i = 1; i < s.size(); i++) {
            while (j > 0 && s[i] != s[j]) { // j要保证大于0，因为下面有取j-1作为数组下标的操作
                j = next[j - 1]; // 注意这里，是要找前一位的对应的回退位置了
            }
            if (s[i] == s[j]) {
                j++;
            }
            next[i] = j;
        }
    }

使用next数组来做匹配

class Solution 
{
public:
    void getNext(int* next, const string& s) 
    {
        int j = 0;
        next[0] = 0;
        for(int i = 1; i < s.size(); i++) //注意i从1开始
        {
            while (j > 0 && s[i] != s[j]) //前后缀不相同了
            {
                j = next[j - 1];
            }
            if (s[i] == s[j]) // 找到相同的前后缀
            {
                j++;
            }
            next[i] = j;// 将j（前缀的长度）赋给next[i]
        }
    }
    //下面用next数组做匹配
    int strStr(string haystack, string needle) 
    {
        if (needle.size() == 0) 
        {
            return 0;
        }
        int next[needle.size()];
        getNext(next, needle);
        int j = 0;
        for (int i = 0; i < haystack.size(); i++) // 注意i就从0开始
        {
            while(j > 0 && haystack[i] != needle[j]) 
            {
                j = next[j - 1];
            }
            if (haystack[i] == needle[j]) 
            {
                j++;
            }
            if (j == needle.size() )// 文本串s里出现了模式串t 
            {
                return (i - needle.size() + 1);
            }
        }
        return -1;
    }
};

例题26：KMP字符串

算法基础（二）（共有30道例题）

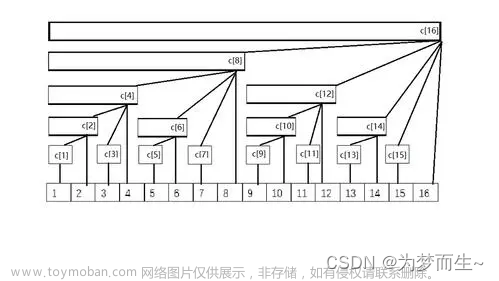
（六）树

（1）二叉树种类

1.1 空的二叉树
1.2 只有根结点的二叉树
1.3 只有左子树或者右子树的二叉树
1.4 左右子树都存在的时候：
（1）满二叉树
（2）完全二叉树：在完全二叉树中，除了最底层节点可能没填满外，其余每层节点数都达到最大值，并且最下面一层的节点都集中在该层最左边的若干位置。若最底层为第 h 层，则该层包含 1~ $2^(h-1)$ 个节点。
算法基础（二）（共有30道例题）

（2）遍历方式

2.1前序遍历（根在前面）
2.2中序遍历（根在中间）
2.3后序遍历（根在后面）算法基础（二）（共有30道例题）

3.C++代码

struct TreeNode //链式储存二叉树
{
    int val;
    TreeNode *left;
    TreeNode *right;
    TreeNode(int x) : val(x), left(NULL), right(NULL) {}
};

1.二叉树之递归遍历

（1）前序遍历

题目难度：简单

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    void Traversal(TreeNode *cur,vector<int> &vec)
    {
        if(cur==nullptr)
        {
            return;//相当于中断，意思是只要cur=null，就退出Traversal函数
        }
        vec.push_back(cur->val);//中
        Traversal(cur->left,vec);
        Traversal(cur->right,vec);
    }
    vector<int> preorderTraversal(TreeNode* root) 
    {
        vector<int> vec;
        Traversal(root,vec);
        return vec;
    }
};

（2）中序遍历

题目难度：简单

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    void Traversal(TreeNode *cur,vector<int> &vec)
    {
        if(cur==nullptr)
        {
            return;//相当于中断
        }
        Traversal(cur->left,vec);
        vec.push_back(cur->val);//中
        Traversal(cur->right,vec);
    }
    vector<int> preorderTraversal(TreeNode* root) 
    {
        vector<int> vec;
        Traversal(root,vec);
        return vec;
    }
};

（3）后序遍历

题目难度：简单

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    void Traversal(TreeNode *cur,vector<int> &vec)
    {
        if(cur==nullptr)
        {
            return;//相当于中断
        }
        Traversal(cur->left,vec);
        Traversal(cur->right,vec);
        vec.push_back(cur->val);
    }
    vector<int> postorderTraversal(TreeNode* root) 
    {
        vector<int> vec;
        Traversal(root,vec);
        return vec;
    }
};

2.二叉树之统一迭代遍历

（1）前序遍历

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 * */

class Solution {
public:
    vector<int> result;
    stack<TreeNode*> sta;
    vector<int> inorderTraversal(TreeNode* root)    
    {
    	if (root != nullptr) sta.push(root);
       
        while(!sta.empty())
        {
            TreeNode *cur=sta.top();
            
            if(cur!=nullptr)
            {
                sta.pop();//先把根结点弹出，防止重复
                 if(cur->right!=nullptr)
                {
                	sta.push(cur->right);//右
                }
				 if(cur->left!=nullptr)
                {
                	sta.push(cur->left);//左
                }
                 sta.push(cur);//中
                sta.push(nullptr);
            
            }
            else
            {
                sta.pop();
                result.push_back(sta.top()->val);
                sta.pop();
            }
        }
        return result;
    }
};

（2）中序遍历

大致可以分为如下四部曲。

root压入栈顶。
将栈顶节点取出，记为cur
判断：栈顶第一个非空节点是否被视作根节点处理过？（cur是否为null？）
如否：进行处理
将当前节点cur作为根节点。
为使出栈时符合左-根-右的顺序，以右-根-左的顺序将节点入栈，具体如下：
(1)将当前节点cur视作根节点，先出栈，以便后续操作
(2)如有右节点则入栈，无则不入
(3)当前节点cur入栈
(4)将空指针nullptr入栈，标志cur已被处理过。同时，如无左节点，结束处理流程。
(5)如有左节点，则左节点进入栈顶，结束处理流程。
注：(2)、(5)确保栈顶始终是cur节点的左节点（若无左节点则为nullptr）。
将重复此步处理，直到cur的左节点为空。此时，cur为下一个应加入result的节点。
如是：则该节点无左子树，或是左子树已被访问完毕。无论如何，现在，该节点应被加入result。
（1）将当前节点cur加入result。
（2）弹出栈顶的cur，以表示此节点已被加入result，无需再次被考虑。文章来源地址https://www.toymoban.com/news/detail-429609.html

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 * */

class Solution {
public:
    vector<int> result;
    stack<TreeNode*> sta;
    vector<int> inorderTraversal(TreeNode* root)    
    {
    	if (root != nullptr) sta.push(root);
       
        while(!sta.empty())
        {
            TreeNode *cur=sta.top();
            
            if(cur!=nullptr)
            {
                sta.pop();//先把根结点弹出，防止重复
                if(cur->right!=nullptr)
                {
                	sta.push(cur->right);//右
                }

                sta.push(cur);//中
                sta.push(nullptr);
                if(cur->left!=nullptr)
                {
                	sta.push(cur->left);//左
                }
            }
            else
            {
                sta.pop();
                result.push_back(sta.top()->val);
                sta.pop();
            }
        }
        return result;
    }
};

（3）后序遍历

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */

class Solution {
public:
    vector<int> result;
    stack<TreeNode*> sta;
    vector<int> postorderTraversal(TreeNode* root) 
    {
        if (root != nullptr) sta.push(root);
        
        while(!sta.empty())
        {
            TreeNode *cur=sta.top();
            if(cur!=nullptr)
            {
                sta.pop();

                sta.push(cur);
                sta.push(nullptr);

                if(cur->right!=nullptr)
                {
                    sta.push(cur->right);
                }
                if(cur->left!=nullptr)
                {
                    sta.push(cur->left);
                }
                
            }
            else
            {
                sta.pop();
                result.push_back(sta.top()->val);
                sta.pop();
            }
        }
        return result;
    }
};

3.二叉树之层序遍历

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    vector<vector<int>> levelOrder(TreeNode* root) 
    {
        queue<TreeNode*> que;
        
        vector<vector<int>> result;

        if(root!=NULL)
        {
            que.push(root);
        }

        while(!que.empty())
        {
            vector<int> vec;
            //vec要放在这里定义，如果放在while外面定义，这样他的生存期就在这个函数里面。
            //等到下次调用这个while函数就可以得到一个空的vec;
            int size=que.size();//本层节点的个数

            while(size--)
            {
                TreeNode *node=que.front();
                
                vec.push_back(node->val);
                que.pop();
                
                if(node->left) que.push(node->left);
                if(node->right) que.push(node->right);
                
            }
            result.push_back(vec);
        }
        return result;
    }
}

到了这里，关于算法基础（二）（共有30道例题）的文章就介绍完了。如果您还想了解更多内容，请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章，希望大家以后多多支持TOY模板网！

算法基础（二）（共有30道例题）

六、数据结构

（一）数组

1.数组之二分查找

例题1：二分查找

例题2：数的范围

例题3：在排序数组中查找元素的第一个和最后一个位置

2.数组之移除元素

例题4：移除元素

（二）链表

1.链表之静态链表(用数组模拟单链表)

例题5：单链表

2.链表之静态链表（用数组模拟双链表）

例题6：双链表

3.链表之删除元素

例题7：移除链表元素：给你一个链表的头节点 head 和一个整数 val ，请你删除链表中所有满足 Node.val == val 的节点，并返回 新的头节点 。

例题8：删除排序链表中的重复元素给定一个已排序的链表的头 head ， 删除所有重复的元素，使每个元素只出现一次 。返回 已排序的链表 。

例题9：删除链表的倒数第N个结点：给你一个链表，删除链表的倒数第 n 个结点，并且返回链表的头结点。

2.链表之交换结点：

例题10： 两两交换链表中的节点：给你一个链表，两两交换其中相邻的节点，并返回交换后链表的头节点。你必须在不修改节点内部的值的情况下完成本题（即，只能进行节点交换）。

3.链表之反转：

例题11：反转链表：给你单链表的头节点 head ，请你反转链表，并返回反转后的链表。

（三）栈

1.用数组模拟栈

例题12：模拟栈

2.栈之单调栈

例题13：单调栈

3.栈与队列的关系

例题14：用栈实现队列

例题15：用两个队列实现栈

补充：用一个队列实现栈

4.栈与匹配

例题16：有效的括号(此题想了很久，最后看了答案)

例题17：删除字符串中的所有相邻重复项

5.栈之逆波兰

例题18：逆波兰表达式求值（输入直接就是后缀表达式）

例题19：表达式求值（输入是中缀表达式）

（四）队列

1.用数组模拟队列

例题19：模拟队列

2.队列之单调队列

例题20：滑动窗口

例题21：滑动窗口最大值

3.队列之优先队列

例题22：前 K 个高频元素

（五）串

1.反转字符串

例题23：反转字符串

例题24：反转字符串 II

2.字符串之双指针

例题25：剑指 Offer 05 替换空格：请实现一个函数，把字符串 s 中的每个空格替换成"%20"。

3.字符串之匹配KMP算法

例题26：KMP字符串

（六）树

（1）二叉树种类

（2）遍历方式

3.C++代码

1.二叉树之递归遍历

（1）前序遍历

（2）中序遍历

（3）后序遍历

2.二叉树之统一迭代遍历

（1）前序遍历

（2）中序遍历

（3）后序遍历

3.二叉树之层序遍历

相关文章

觉得文章有用就打赏一下文章作者

支付宝扫一扫打赏

微信扫一扫打赏

支付宝扫一扫领取红包，优惠每天领

二维码1

二维码2

例题7：移除链表元素：给你一个链表的头节点 head 和一个整数 val ，请你删除链表中所有满足 Node.val == val 的节点，并返回新的头节点。

例题8：删除排序链表中的重复元素给定一个已排序的链表的头 head ，删除所有重复的元素，使每个元素只出现一次。返回已排序的链表。

例题10：两两交换链表中的节点：给你一个链表，两两交换其中相邻的节点，并返回交换后链表的头节点。你必须在不修改节点内部的值的情况下完成本题（即，只能进行节点交换）。