参考书籍:陈强.机器学习及R应用.北京:高等教育出版社,2020
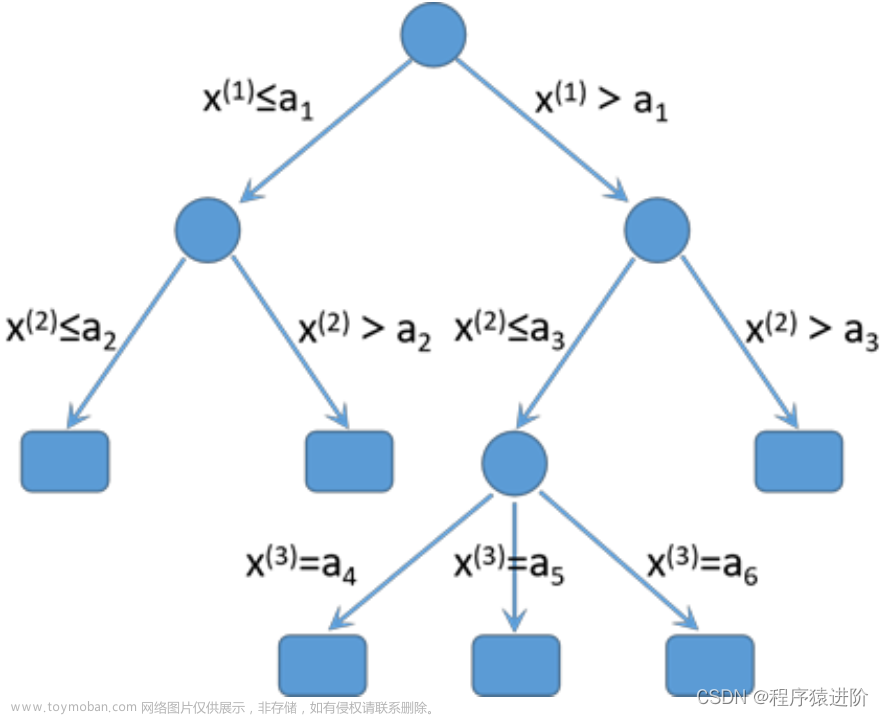
“决策树"算法是一种非参数方法,它本质上也是一种“近邻”方法,因此本章分别介绍运用于回归问题以及分类问题的决策树算法。
一 回归树
在本例中,使用Boston房价数据,该数据集包含1970年波士顿506个社区有关房价的14个变量,响应变量为社区房价中位数medv,下面使用rpart包估计决策树,该算法与CART非常接近。部分数据集及R代码如下所示。

#估计回归树
library(rpart)
library(MASS)
dim(Boston) #506个观测,14个变量
#[1] 506 14
set.seed(1)
train<-sample(506,354) #随机选取354个观测值(70%)作为训练集,其余作为测试集
set.seed(123)
fit<-rpart(medv~.,data = Boston,subset = train)
fit #结果展示如下,默认进行10折交叉验证
#n= 354
node), split, n, deviance, yval
* denotes terminal node
1) root 354 32268.9600 22.95085
2) rm< 6.945 296 10831.8100 19.82230
4) lstat>=14.405 119 2214.7900 14.84202
8) crim>=5.76921 56 636.1371 12.04286 *
9) crim< 5.76921 63 749.8527 17.33016 *
5) lstat< 14.405 177 3681.0470 23.17062
10) rm< 6.543 138 1690.0800 21.85580 *
11) rm>=6.543 39 908.2292 27.82308 *
3) rm>=6.945 58 3754.2630 38.91724
6) rm< 7.445 33 749.6655 33.12727 *
7) rm>=7.445 25 438.0200 46.56000 *通过结果,显示出共有11节点,而后跟”*“号则为终节点,每行输出结果的内容依次为:node(节点)、split(到节点的分裂条件),n(该节点的样本数),deviance(该节点的偏离度,对回归问题就是残差平方和),yval(该节点的预测值,即y的平均值)。但是这样的结果没有这么直观,因此可用图像的形式加以表述。
#决策树图像
op<-par(no.readonly = TRUE)
par(mar=c(1,1,1,1)) #设置图像的英分单位
plot(fit,margin = 0.1) #参数margin表示在决策树的边框留下0.1的空间
text(fit) #在图像中加入文字信息
par(op)
该图像的右边表示“是”,左边表示“否",如根节点的分裂条件为房间数“rm<6.945”。如果不满足此条件’则为“大宅”向右,满足条件“rm>=6.945”的大宅又可进一步细分为“rm>=7.445“的“豪宅”以及满足“rm<7.445“的—般大宅。该图还显示终节点“豪宅’,的预测均价为46.56而终节点“—般大宅”的预测均价为33.13.
数据集总有13个特征变量,但此决策树仅用了3个变量,对于树规模的合理确定,可使决策树拥有更好的泛化预测能力,可用交叉验证来确定。
#确定决策树规模
plotcp(fit)
在交叉验证误差图中,下方横轴为复杂性参数cp,控制对模型复杂度的惩罚力度,上方横轴为决策树规模,即终节点的数目,纵轴为交叉验证误差。
在此图中显示终节点数目为6时,交叉验证误差最低,如果使用“一个标准误(1SE)”的规则,则应选择终节点数目为5,图中虚线表示离最优cp值一个标准差的位置,此图的具体信息还可通过cptable来查看,过程如下:
fit$cptable
fit$cptable
# CP nsplit rel error xerror xstd
1 0.54798440 0 1.0000000 1.0079393 0.09789436
2 0.15296356 1 0.4520156 0.4815081 0.04954874
3 0.07953702 2 0.2990520 0.3307847 0.03894189
4 0.03355353 3 0.2195150 0.2525102 0.03664166
5 0.02568412 4 0.1859615 0.2267945 0.03582720
6 0.01000000 5 0.1602774 0.1959728 0.03280781其中第1列为复杂性参数CP:第2列nsplit为分裂数,也就是终节点数目减1;第3列rel error为训练集的相对误差;第4列xerror为交叉验证误差;第5列xstd为交叉验证误差的标准误。
为得到修枝后的最优模型,需提取能使交叉验证误差xerror最小化的最优复杂性参数cp,如下所示:
#决策树修枝
min_cp<-fit$cptable[which.min(fit$cptable[,"xerror"]),"CP"] #选出xerror最小cp值
min_cp
#[1] 0.01
fit_best<-prune(fit,cp=min_cp) #使用修枝函数,得到最终决策树
library(rpart.plot)
prp(fit_best,type=2) #画出修枝后的最优决策树图像,type可设为1-5
下面,对测试集进行预测,并计算测试误差:
tree.pred<-predict(fit_best,newdata = Boston[train,])
y.test<-Boston[-train,"medv"]
mean((tree.pred-y.test)^2)
#[1] 36.2319
plot(tree.pred,y.test,main = "Boston Housing")
abline(0,1)通过结果可知测试集的均方误为36.23,因此画出测试集效应变量的实际值与预测值的散点图:
(abline(0,1)表示直线“y=0+1*x”)

如图所见,此回归树模型只有6个预测值,而实际值变化较大。因此尝试用”一个标准差“的规则来预测,在修枝时,可通过设定参数cp=0.03来实现
#1SE规则
fit_1se<-prune(fit,cp=0.03)
tree.pred.1se<-predict(fit_1se,newdata = Boston[-train,])
mean((tree.pred.1se-y.test)^2)
#[1] 38.17137然而,测试集的均方误差反而上升至38.17,最后作为对比,考察线性回归(ols)模型的测试误差:
#ols
ols.fit<-lm(medv~.,Boston,subset = train)
ols.pred<-predict(ols.fit,newdata = Boston[-train,])
mean((ols.pred-y.test)^2)
#[1] 27.31196结果显示,ols回归的测试集均方误差仅为27.31,明显低于回归树的均方误差,进一步直观地展示ols的预测效果
plot(ols.pred,y.test,main = "OLS Prediction")
abline(0,1)
从图可见,与决策树的6个预测值相比,OLS的预测值更为多样化,故图中的散点更为紧密地围绕在45度线周围。虽然在此例中,决策树的预测效果不及线性回归,但基于决策树的随机森林却明显优于OLS。
二 分类树
在本例中,使用葡萄牙银行市场营销的数据集来演示分类树的R操作,部分数据集及操作过程如下所示:

bank <- read.csv("bank-additional.csv",header = TRUE,sep=";")
str(bank,vec.len=1)
#'data.frame': 4119 obs. of 21 variables:
$ age : int 30 39 ...
$ job : chr "blue-collar" ...
$ marital : chr "married" ...
$ education : chr "basic.9y" ...
$ default : chr "no" ...
$ housing : chr "yes" ...
$ loan : chr "no" ...
$ contact : chr "cellular" ...
$ month : chr "may" ...
$ day_of_week : chr "fri" ...
$ duration : int 487 346 ...
$ campaign : int 2 4 ...
$ pdays : int 999 999 ...
$ previous : int 0 0 ...
$ poutcome : chr "nonexistent" ...
$ emp.var.rate : num -1.8 1.1 ...
$ cons.price.idx: num 92.9 ...
$ cons.conf.idx : num -46.2 -36.4 ...
$ euribor3m : num 1.31 ...
$ nr.employed : num 5099 ...
$ y : chr "no" ...函数str()的参数“vec.1en=1”限制作为示例的观测值个数,默认值为4。结果显示,此数据框包含4119个观测值与21个变量,其中,响应变量Y为因子(取值为”yes“或"no“)’表示在接到银行的直销电话后,客户是否会购买“银行定期存款"产品。特征变量包括客户的个人特征,比如年龄、职业
类型、婚姻状况、教育程度;经济状况,比如是否有信用违约、是否有房贷,是否有个人贷款,工作单位人数;营销状态 ,比如自上次联络以来的天数等。
特别地’特征变量duration表示自上次去电后过了多少秒,显然,在去电前,这个变量对于预测客户购买意愿毫无意义,故从数据框中去掉:
bank$duration<-NULL
prop.table(table(bank$y)) #考虑样本中有购买金融产品意愿的比例
# no yes
0.8905074 0.1094926 结果显示,只有10.9%的客户有购买银行定期存款的意愿。下面,我们把样本随机分为两组保留1000个观测值作为测试集’而以其余3119个观测值为训练集,并使用rpart()函数估计分类树,画出交叉验证图,结果如下所示:
set.seed(1)
train <- sample(4119,3119) #随机选择3119组观测作为训练集
library(rpart)
set.seed(123)
fit <- rpart(y~.,data=bank,subset=train)
plotcp(fit)
使用rpart()函数无须区别分类树或回归树,因为它会根据响应变量的类型自动识别。也可用参数“method=class”指定分类树;或用参数“method=ANOVA”指定回归树。
由图可见,当分类树规模,也就是终节点数目为3时,交叉验证误差达到最小值,进一步可显示交叉验证的细节:
#交叉验证细节
fit$cptable
# CP nsplit rel error xerror xstd
1 0.06051873 0 1.0000000 1.0000000 0.05060858
2 0.01056676 2 0.8789625 0.8904899 0.04808341
3 0.01008646 5 0.8472622 0.9769452 0.05009393
4 0.01000000 7 0.8270893 0.9769452 0.05009393
min_cp <- fit$cptable[which.min(fit$cptable[,"xerror"]),"CP"]
min_cp
#[1] 0.01056676结果显示,当复杂性参数CP等于0.01056676,分裂数nsplit为2(故终节点数为3)时,交叉验证误差xerror达到最小。因此估计修枝后的最优模型,并画此分类树的结构图:
fit_best <- prune(fit, cp = min_cp) #最优决策树
op <- par(no.readonly = TRUE)
par(mar=c(1,1,1,1))
plot(fit_best,uniform=TRUE,margin=0.1)
text(fit_best,cex=1.5)
par(op)
参数“uniform=TRUE”表示使不同节点垂直下降的高度保持一致(默认与基尼指数的下
降幅度成正比)。
图中的决策树只有3个终节点,这意味着只要给这一类客户致电即可,即工作单位人数小于5088人,而且自上次营销致电已过去12.5天的客户。
下面,在测试集中进行预测,并展示混淆矩阵:
#测试集预测
tree.pred <- predict(fit_best,bank[-train,],type="class")
y.test <- bank[-train,"y"]
(table <- table(tree.pred,y.test))
# y.test
tree.pred no yes
no 890 87
yes 6 17
(accuracy <- sum(diag(table))/sum(table)) #准确率
#[1] 0.907
(sensitivity <- table[2,2]/(table[1,2]+table[2,2])) #灵敏度
#[1] 0.1634615结果显示,虽然预测准确率(accuracy)高达90.7%;但算法的灵敏度(sensitivity)仅有16.3%,即只能成功识别16.3%有购买意向的客户。因为无购买意向的客户占比达到89.1%,故只要猜想所有客户都不够买,即可达到89.1%的准确率。
在做以上预测时可默认以“概率大于0.5”作为预测标准。为提高算法的灵敏度,以识别更多有购买意向的潜在客户’可降低此概率门槛值,比如将“概率大于0.1”即视为有购买意向。为此’输人以下命令:
tree.prob <- predict(fit_best,bank[-train,],type="prob")
tree.pred <- tree.prob[,2] >= 0.1
(table <- table(tree.pred,y.test))
# y.test
tree.pred no yes
FALSE 826 59
TRUE 70 45
(accuracy <- sum(diag(table))/sum(table))
#[1] 0.871
(sensitivity <- table[2,2]/(table[1,2]+table[2,2]))
#[1] 0.4326923函数rpart()默认使用基尼系数估计分类树,下面尝试使用信息(parms=list(split="information"))作为分裂准则,结果显示所得的混淆矩阵及预测率都与基尼指数结果完全相同。
#信息熵准则
set.seed(123)
fit <- rpart(y~.,data=bank,subset=train,parms=list(split="information"))
min_cp <- fit$cptable[which.min(fit$cptable[,"xerror"]),"CP"]
fit_best <- prune(fit, cp = min_cp)
tree.pred <- predict(fit_best,bank[-train,],type="class")
(table <- table(tree.pred,y.test))
# y.test
tree.pred no yes
no 890 87
yes 6 17
(accuracy <- sum(diag(table))/sum(table))
#[1] 0.907为了避免过拟合,函数rpart()还设置了默从的参数值“minsplit=20”,表示如果节点样本数少于20即不再分裂;以及“minbucket=5”表示终节点至少应包含5个观测值。下面尝试去掉这两个限制,再次进行预测:文章来源:https://www.toymoban.com/news/detail-429865.html
#去限制
set.seed(123)
fit <- rpart(y~.,data=bank,subset=train,control=rpart.control(minsplit = 0,minbucket = 0))
min_cp <- fit$cptable[which.min(fit$cptable[,"xerror"]),"CP"]
fit_best <- prune(fit, cp = min_cp)
tree.pred <- predict(fit_best,bank[-train,],type="class")
(table <- table(tree.pred,y.test))
# y.test
tree.pred no yes
no 890 87
yes 6 17
(accuracy <- sum(diag(table))/sum(table))
#[1] 0.907其中,函数rpart()的参数“control=rpart.control(minsplit = 0,minbucket = 0))”,表示既不限制节点分裂的前提条件,也不限制终节点的规模。结果显示,变动这两个参数,对于混淆矩阵与预测准确率并无影响。可能的原因是,虽然未限制节点分裂条件与终节点规模,或许导致过拟合(决策树过于枝繁叶茂),但经过交叉验证进行修枝后,模型的复杂性依然能得到合理控制。文章来源地址https://www.toymoban.com/news/detail-429865.html
到了这里,关于R语言机器学习篇——决策树的文章就介绍完了。如果您还想了解更多内容,请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章,希望大家以后多多支持TOY模板网!