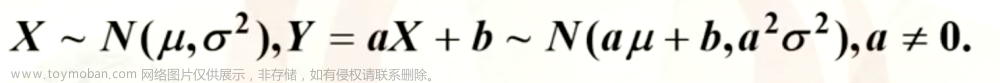概论第6章_正态总体的抽样分布_样本均值的期望与样本方差的期望_

这篇具有很好参考价值的文章主要介绍了概论第6章_正态总体的抽样分布_样本均值的期望与样本方差的期望__方差的期望。希望对大家有所帮助。如果存在错误或未考虑完全的地方，请大家不吝赐教，您也可以点击"举报违法"按钮提交疑问。

下面的定理给出 样本均值的期望，方差的期望，样本方差的期望, 它不依赖于总体的分布形式。

一. 定理：

假设有总体X, 均值 $\mu$ , E(X)= $\mu$ , 有方差 $\sigma^2$ , $\space$ D(X) = $\sigma^2$ $<+\infty$ 。
$X_1, X_2, ... X_n$ 为来自X的样本，n为样本容量, $\overline x$ 表示样本均值， $S^2$ 表示样本方差，则有

1. $E(\overline x) =$ $\mu$ , 即样本均值的期望等于总体均值

2. $D(\overline x) =$ $\frac{\sigma^2}{n}$ ，样本均值的方差等于总体方差除以样本容量

3. $E(S^2) =$ $\sigma^2$ , 样本方差的期望等于总体方差

4. $D(S^2)=$ $\frac{2\sigma^4}{n-1}$

定理表明： 样本均值的期望与总体均值相同，样本均值的方差是总体方差的 $\frac{1}{n}$ , 即 $D(\overline x) =$ $\frac{D(X)}{n}$

二. 看例题

设 $x_1, x_2, ...,x_8$ 是从正态总体N(10, 9)中抽取的样本，试求样本均值 $\space \overline x$ 的标准差。

解: $\space\space \sqrt {D(x)} =$ $\sqrt{\frac{\sigma^2}{n}}$ = $\sqrt{\frac{9}{8}}$ = $\frac{3}{2\sqrt{2}}$ .

从正态总体N(3.4, 36)中抽取容量为 n 的样本，如果要求其样本均值位于区间(1.4, 5.4)内的概率不小于 0.95, 问样本容量 n 至少应取多大？
附表：标准正态分布表

解：依题意，需要求P{1.4< $\overline x$ <5.4} $\geqslant$ 0.95,
设样本均值为 $\overline x$
因为 P{X在a到b之间} = $\Phi(\frac{b-\mu}{\sigma}) - \Phi(\frac{a-\mu}{\sigma})$ ,
已知 $\mu = 3.4$ ,

P{1.4< x ‾ \overline x x<5.4} = Φ ( 5.4 − 3.4 6 n ) − Φ ( 1.4 − 3.4 6 n ) \Phi(\frac{5.4-3.4}{\frac{6}{\sqrt{n}}}) - \Phi(\frac{1.4-3.4}{\frac{6}{\sqrt{n}}}) Φ(n 65.4−3.4)−Φ(n 61.4−3.4) = Φ ( 2 6 n ) − Φ ( − 2 6 n ) \Phi(\frac{2}{\frac{6}{\sqrt{n}}}) - \Phi(\frac{-2}{\frac{6}{\sqrt{n}}}) Φ(n 62)−Φ(n 6−2) = Φ ( n 3 ) − Φ ( − n 3 ) \Phi(\frac{\sqrt{n}}{3}) - \Phi(-\frac{\sqrt{n}}{3}) Φ(3n )−Φ(−3n ) （1）

因为 $\Phi(a) = 1- \Phi(-a)$ ,
(1)式 = 2 $\Phi(\frac{\sqrt{n}}{3}) - 1\geqslant0.95$

有， $\Phi(\frac{\sqrt{n}}{3}) \geqslant0.975$ ，
查表格，有 $\frac{\sqrt{n}}{3} \geqslant1.96$ , $n\geqslant 34.5744$
所以样本容量n 至少为35.
~~~文章来源地址https://www.toymoban.com/news/detail-429895.html