数学建模——插值与拟合-Toy模板网

这篇具有很好参考价值的文章主要介绍了数学建模——插值与拟合。希望对大家有所帮助。如果存在错误或未考虑完全的地方，请大家不吝赐教，您也可以点击"举报违法"按钮提交疑问。

插值与拟合在建模过程中是一种十分重要的方法，由于赛题中给出的数据可能出现缺失，此时就需要用到插值的方式来对数据进行补全，又或者是给出一部分数据，需要你对未来一部分数据进行预测，这个时候就需要用到拟合的相关知识。

插值篇：

在实际中，常常要处理由实验或测量所得到的一些离散数据。插值与拟合方法就是要通过这些数据去确定某一类已知函数的参数或寻求某个近似函数，使所得到的近似函数与已知数据有较高的拟合精度。如果要求这个近似函数（曲线或曲面）经过所已知的所有数据点，则称此类问题为插值问题。（不需要函数表达式）

在MATLAB中提供了一些内置函数来实现插值，如interp1(一维插值)、intero2(二维插值)、interp3(三维插值)等等

一维插值使用方法：

yi：在xi处插值的结果

x，y：插值节点

xi：被插值点

method：插值方法（‘nearest’最邻近插值，‘linear’线性插值，‘spline’三次样条插值，‘cubic’立方插值，当缺省时为分段线性插值）

具体案例：

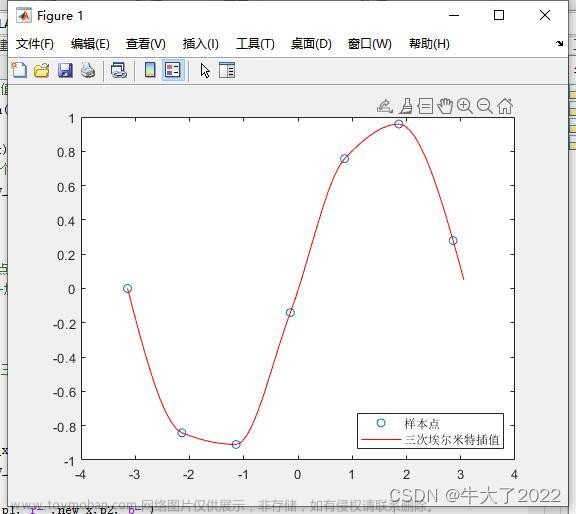
这就是一个典型的插值问题，只给出一部分数据，让我们把每个数据点之间的数据估计出来，我们可以使用interp1命名解决，代码如下：

x = 1:12;
y = [5 8 9 15 25 29 31 30 22 25 27 24];
xi = 1:0.01:12;
yi = interp1(x,y,xi,'spline');
plot(x,y,'*',xi,yi,'r')
xlabel('时间')，ylabel('温度')

我们可以得到如下结果：（是不是非常简单便捷(✪ω✪)）

数学建模——插值与拟合

看完一维插值，我们一起瞅瞅二维插值吧！

二维插值使用方法：

x0、y0、z0：插值节点

x、y：被插值点

method：插值方法（‘nearest’最邻近插值，‘linear’双线性插值、‘cubic’双三次插值、缺省时为双线性插值）

举个栗子吧：数学建模——插值与拟合

对于上面这个问题，我们可以采用二维插值的方式来进行处理：

%%绘制原图

x = 1:5;
y = 1:3;
wendu = [82 81 80 82 84;
         79 63 61 65 81;
         84 84 82 85 86];
%mesh(x,y,wendu)

%%开始插值

xi = 1:0.2:5;
yi = 1:0.2:3;
zi = interp2(x,y,wendu,xi',yi,'cubic');
mesh(xi,yi,zi)

插值前：

数学建模——插值与拟合

插值后：

数学建模——插值与拟合

区别还是很明显的，一目了然，插值篇到这里就结束了，接下来我们进入拟合篇！

拟合篇：

对于已给一批实测数据，由于实测方法、实验环境等一些外界因素的影响，不可避免地会产生随机干扰和误差。我们自然希望根据数据分布的总趋势去剔除观察数据中的偶然误差，这就是所谓的数据修匀（或称数据平滑）问题。

同样，在MATLAB中也存在着拟合函数的内置函数，如对多项式： $数学建模——插值与拟合$ 进行拟和

可利用已有程序：a = ployfit(x,y,m) 注意：m为拟合多项式的次数

多项式在x出的值y可以用以下命令计算：y = ployval(a,x)

此处给出一个代码实例：

x = 0:0.1:1;
y = [-0.447 1.978 3.28 6.16 7.08 7.34 7.66 9.56 9.48 9.30 11.2];
A = polyfit(x,y,2)   %A为拟合出来的函数
z = polyval(A,x);    %求多项式在x处的值z
plot(x,y,'k+',x,z,'r')

拟合结果如下：

数学建模——插值与拟合