二叉树C语言实现

最新代码仓库：https://github.com/sixsixQAQ/binary-tree

一、指针 VS 数组+索引

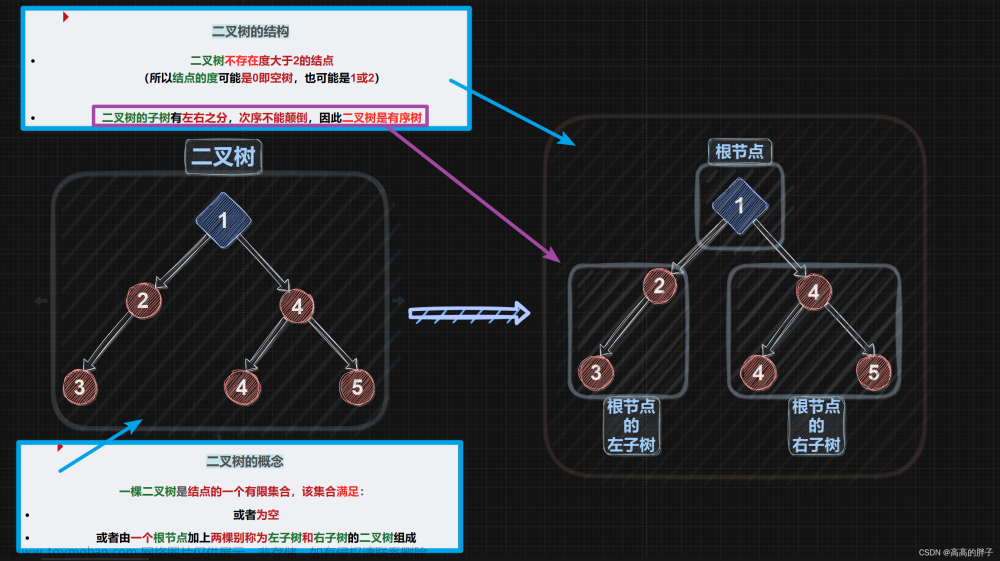
二叉树的实现，既可以用数组 + 索引来实现，也可以用指针来实现。

指针实现比索引+数组实现有天然的优势：

1. 指针可以用NULL判空，无序另设判空用的值。

   • 比如索引实现时，通常需要用-1来表示非法索引/空索引。

2. 指针实现传参更少。

   • 比如指针可以很方便地递归，只要tree->lchild就可以递归下一个子树；
   • 而索引实现时，当前树如果想要递归到子树，总是需要再传一个索引来递归。
   • 这是因为指针直指内存，而数组 + 索引才能实现这一效果，比如tree->lchild，用数组+索引表达就是tree[index].lchild，更像是在模拟指针。

3. 指针实现的代码更清晰。

   • 单纯更清晰而已，用索引会出现多层的方括号，信息密度高，可读性差。

指针实现见在后文。

仓库的还提供了一个数组+索引实现的版本供参考，接口和指针实现差不多。

可以先看看下面一个小小对比，指针更方便：

#include <stdlib.h>
#include <stdio.h>

typedef struct binary_tree_I binary_tree_I;
struct binary_tree_I {
	char data;
	int lchild, rchild;
};

typedef struct binary_tree_P binary_tree_P;
struct binary_tree_P {
	char data;
	binary_tree_P *lchild, *rchild;
};


binary_tree_P *
get_lchild_P (binary_tree_P *tree)
{
	return tree->lchild;
}

binary_tree_P *
get_rchild_P (binary_tree_P *tree)
{
	return tree->rchild;
}

binary_tree_I *
get_lchild_I (binary_tree_I *tree, int curr)
{
	return &tree[ tree[curr].lchild ];
}

binary_tree_I *
get_rchild_I (binary_tree_I *tree, int curr)
{
	return &tree[ tree[curr].rchild];
}

int
main (void)
{

}

二、指针实现

main.c：

#include <stdio.h>
#include <string.h>
#include "binary_tree.h"


void
print_all (binary_tree_node *tree)
{
	printf ("先序遍历: "), binary_tree_print_data (tree, DLR), putchar ('\n');
	printf ("中序遍历: "), binary_tree_print_data (tree, LDR), putchar ('\n');
	printf ("后序遍历: "), binary_tree_print_data (tree, LRD), putchar ('\n');
	printf ("层序遍历: "), binary_tree_print_data (tree, LEVEL), putchar ('\n');
	
	printf ("打印树： "), binary_tree_print_tree (tree), putchar ('\n');
	
	printf ("结点数：%d\n", binary_tree_get_node_count (tree));
	printf ("叶子结点数：%d\n", binary_tree_get_leaf_node_count (tree));
	printf ("树深：%d\n", binary_tree_get_tree_depth (tree));
}

int
main (void)
{

	/**
	 * Demo
	 *                  A
	 *                /   \
	 *              B      G
	 *            /  \    / \
	 *          C     F  H   I
	 *        /
	 *      D
	 *       \
	 *        E
	*/
	
	{
		char DLR_data[] = {'A', 'B', 'C', 'D', -1, 'E', -1, -1, -1, 'F', -1, -1, 'G', 'H', -1, -1, 'I', -1, -1};
		binary_tree_node *tree = binary_tree_new_DLR (DLR_data);
		
		print_all (tree);
		
		binary_tree_delete (tree);
	}
	
	{
		puts ("--------------重建树--------------：");
		char *DLR_sequence = "ABCDEFGHI";
		char *LDR_sequence = "DECBFAHGI";
		
		binary_tree_node *tree = binary_tree_rebuild_from_DLR_and_LDR (
		                             DLR_sequence, LDR_sequence, strlen (DLR_sequence)
		                         );
		                         
		print_all (tree);
		
		binary_tree_delete (tree);
	}
	puts ("----------------------------------------------------------");
	
	
	
	/**
	 * Demo 2
	 *                  A
	 *                /   \
	 *              B      C
	 *            /  \    / \
	 *          D     E  F   G
	 *           \      / \
	 *            H    I   J
	*/
	{
		char DLR_data[] = {'A', 'B', 'D', -1, 'H', -1, -1, 'E', -1, -1, 'C', 'F', 'I', -1, -1, 'J', -1, -1, 'G', -1, -1};
		binary_tree_node *tree = binary_tree_new_DLR (DLR_data);
		print_all (tree);
		binary_tree_delete (tree);
	}
	{
		puts ("--------------重建树--------------：");
		char *DLR_sequence = "ABDHECFIJG";
		char *LDR_sequence = "DHBEAIFJCG";
		
		binary_tree_node *tree = binary_tree_rebuild_from_DLR_and_LDR (
		                             DLR_sequence, LDR_sequence, strlen (DLR_sequence)
		                         );
		                         
		print_all (tree);
		
		binary_tree_delete (tree);
	}
}

输出结果：

先序遍历: A B C D E F G H I 
中序遍历: D E C B F A H G I 
后序遍历: E D C F B H I G A 
层序遍历: A B G C F H I D E 
打印树： A(B(C(D(,E)),F),G(H,I))
结点数：9
叶子结点数：4
树深：5
--------------重建树--------------：
先序遍历: A B C D E F G H I 
中序遍历: D E C B F A H G I 
后序遍历: E D C F B H I G A 
层序遍历: A B G C F H I D E 
打印树： A(B(C(D(,E)),F),G(H,I))
结点数：9
叶子结点数：4
树深：5
----------------------------------------------------------
先序遍历: A B D H E C F I J G 
中序遍历: D H B E A I F J C G 
后序遍历: H D E B I J F G C A 
层序遍历: A B C D E F G H I J 
打印树： A(B(D(,H),E),C(F(I,J),G))
结点数：10
叶子结点数：5
树深：4
--------------重建树--------------：
先序遍历: A B D H E C F I J G 
中序遍历: D H B E A I F J C G 
后序遍历: H D E B I J F G C A 
层序遍历: A B C D E F G H I J 
打印树： A(B(D(,H),E),C(F(I,J),G))
结点数：10
叶子结点数：5
树深：4

binary_tree.h：

#ifndef BINARY_TREE_H
#define BINARY_TREE_H

#include <stdbool.h>
#include <stddef.h>

typedef char data_type;

typedef struct binary_tree_node binary_tree_node;
struct binary_tree_node {
	data_type data;
	binary_tree_node *lchild, *rchild;
};

binary_tree_node *binary_tree_new_DLR (const data_type *data_array);

void binary_tree_delete (binary_tree_node *tree);

void binary_tree_traverse_DLR (binary_tree_node *tree,
                               void (*solve) (binary_tree_node *, void *),
                               void *arg);
void binary_tree_traverse_LDR (binary_tree_node *tree,
                               void (*solve) (binary_tree_node *, void *),
                               void *arg);
void binary_tree_traverse_LRD (binary_tree_node *tree,
                               void (*solve) (binary_tree_node *, void *),
                               void *arg);
void binary_tree_traverse_level (binary_tree_node *tree,
                                 void (*solve) (binary_tree_node *, void *),
                                 void *arg);

void binary_tree_traverse_DLR_const (const binary_tree_node *tree,
                                     void (*solve) (const binary_tree_node *, void *),
                                     void *arg);
void binary_tree_traverse_LDR_const (const binary_tree_node *tree,
                                     void (*solve) (const binary_tree_node *, void *),
                                     void *arg);
void binary_tree_traverse_LRD_const (const binary_tree_node *tree,
                                     void (*solve) (const binary_tree_node *, void *),
                                     void *arg);
void binary_tree_traverse_level_const (const binary_tree_node *tree,
                                       void (*solve) (const binary_tree_node *, void *),
                                       void *arg);

bool binary_tree_is_leaf_node (const binary_tree_node *node);

int binary_tree_get_node_count (const binary_tree_node *tree);

int binary_tree_get_leaf_node_count (const binary_tree_node *tree);

int binary_tree_get_tree_depth (const binary_tree_node *tree);

typedef enum binary_tree_traverse_order {
	DLR, LDR, LRD, LEVEL
} binary_tree_traverse_order;

void binary_tree_print_tree (const binary_tree_node *tree);
void binary_tree_print_data (const binary_tree_node *tree, binary_tree_traverse_order order);

binary_tree_node *binary_tree_rebuild_from_DLR_and_LDR (
    const data_type *DLR_sequence,
    const data_type *LDR_sequence,
    size_t length
);



#endif // BINARY_TREE_H

binary_tree.c：文章来源地址https://www.toymoban.com/news/detail-430020.html

#include "binary_tree.h"
#include <stdlib.h>
#include <stddef.h>
#include <stdio.h>
#include <string.h>

static inline void *
Malloc (size_t size)
{
	void *mem = malloc (size);
	if (mem == NULL) {
		fprintf (stderr, "malloc() failed");
		exit (EXIT_FAILURE);
	}
	return mem;
}

static const data_type EMPTY_BRANCH = -1;

static binary_tree_node *
real_binary_tree_new_DLR (const data_type *data_array, int *curr)
{
	binary_tree_node *tree;
	if (data_array[*curr] == EMPTY_BRANCH) {
		tree = NULL, ++*curr;
	} else {
		tree = Malloc (sizeof (binary_tree_node));
		tree->data = data_array[*curr], ++*curr;
		tree->lchild = real_binary_tree_new_DLR (data_array, curr);
		tree->rchild =  real_binary_tree_new_DLR (data_array, curr);
	}
	return tree;
}

binary_tree_node *
binary_tree_new_DLR (const data_type *data_array)
{
	int beg = 0;
	return real_binary_tree_new_DLR (data_array, &beg);
}

void
binary_tree_delete (binary_tree_node *tree)
{
	if (tree == NULL)
		return;
	else {
		binary_tree_delete (tree->lchild);
		binary_tree_delete (tree->rchild);
		free (tree);
	}
}

void
binary_tree_traverse_DLR (binary_tree_node *tree, void (*solve) (binary_tree_node *, void *), void *arg)
{
	if (tree == NULL)
		return;
	solve (tree, arg);
	binary_tree_traverse_DLR (tree->lchild, solve, arg);
	binary_tree_traverse_DLR (tree->rchild, solve, arg);
}

void
binary_tree_traverse_LDR (binary_tree_node *tree, void (*solve) (binary_tree_node *, void *), void *arg)
{
	if (tree == NULL)
		return;
	binary_tree_traverse_LDR (tree->lchild, solve, arg);
	solve (tree, arg);
	binary_tree_traverse_LDR (tree->rchild, solve, arg);
}

void
binary_tree_traverse_LRD (binary_tree_node *tree, void (*solve) (binary_tree_node *, void *), void *arg)
{
	if (tree == NULL)
		return;
	binary_tree_traverse_LRD (tree->lchild, solve, arg);
	binary_tree_traverse_LRD (tree->rchild, solve, arg);
	solve (tree, arg);
}

void
binary_tree_traverse_DLR_const (const binary_tree_node *tree,
                                void (*solve) (const binary_tree_node *, void *),
                                void *arg)
{
	binary_tree_traverse_DLR (
	    (binary_tree_node *) tree,
	    (void (*) (binary_tree_node *, void *)) solve,
	    arg
	);
}

void
binary_tree_traverse_LDR_const (const binary_tree_node *tree,
                                void (*solve) (const binary_tree_node *, void *),
                                void *arg)
{
	binary_tree_traverse_LDR (
	    (binary_tree_node *) tree,
	    (void (*) (binary_tree_node *, void *)) solve,
	    arg
	);
}

void
binary_tree_traverse_LRD_const (const binary_tree_node *tree,
                                void (*solve) (const binary_tree_node *, void *),
                                void *arg)
{
	binary_tree_traverse_LRD (
	    (binary_tree_node *) tree,
	    (void (*) (binary_tree_node *, void *)) solve,
	    arg
	);
}

bool
binary_tree_is_leaf_node (const binary_tree_node *node)
{
	if (node == NULL)
		return false;
	else
		return node->lchild == NULL && node->rchild == NULL;
}



static void inline
callback_INC_node_count (const binary_tree_node *tree, void *count)
{
	++* (int *) count;
}

int
binary_tree_get_node_count (const binary_tree_node *tree)
{
	int count = 0;
	binary_tree_traverse_DLR_const (tree, callback_INC_node_count, &count);
	return count;
}

static void inline
callback_INC_leaf_node_count (const binary_tree_node *tree, void *count)
{
	if (binary_tree_is_leaf_node (tree))
		++* (int *) count;
}

int
binary_tree_get_leaf_node_count (const binary_tree_node *tree)
{
	int count = 0;
	binary_tree_traverse_DLR_const (tree, callback_INC_leaf_node_count, &count);
	return count;
}

int
binary_tree_get_tree_depth (const binary_tree_node *tree)
{
	if (tree == NULL)
		return 0;
	else {
		int ldepth = binary_tree_get_tree_depth (tree->lchild);
		int rdepth = binary_tree_get_tree_depth (tree->rchild);
		if (ldepth > rdepth)
			return ldepth + 1;
		else
			return rdepth + 1;
	}
}

typedef
void (*binary_tree_traverse_func) (
    binary_tree_node *, void (*) (binary_tree_node *, void *), void *
);

typedef
void (*binary_tree_traverse_func_const) (
    const binary_tree_node *, void (*) (const binary_tree_node *, void *), void *
);

static binary_tree_traverse_func
get_traverse_func (binary_tree_traverse_order order)
{
	static binary_tree_traverse_func func_array[4] = {NULL};
	
	if (func_array[0] == NULL) {
		func_array[DLR] = binary_tree_traverse_DLR;
		func_array[LDR] = binary_tree_traverse_LDR;
		func_array[LRD] = binary_tree_traverse_LRD;
		func_array[LEVEL] = binary_tree_traverse_level;
	}
	
	return func_array[order];
}

static binary_tree_traverse_func_const
get_traverse_func_const (binary_tree_traverse_order order)
{
	static binary_tree_traverse_func_const func_array[4] = {NULL};
	
	if (func_array[0] == NULL) {
		func_array[DLR] = binary_tree_traverse_DLR_const;
		func_array[LDR] = binary_tree_traverse_LDR_const;
		func_array[LRD] = binary_tree_traverse_LRD_const;
		func_array[LEVEL] = binary_tree_traverse_level_const;
	}
	
	return func_array[order];
}

static void
callback_print_node_data (const binary_tree_node *tree, void *unused)
{
	printf ("%c ", tree->data);
}

void
binary_tree_print_data (const binary_tree_node *tree, binary_tree_traverse_order order)
{
	binary_tree_traverse_func_const func = get_traverse_func_const (order);
	func (tree, callback_print_node_data, NULL);
}

void
binary_tree_print_tree (const binary_tree_node *tree)
{
	if (tree == NULL)
		return;
	putchar (tree->data);
	if (tree->lchild != NULL) {
		putchar ('(');
		
		binary_tree_print_tree (tree->lchild);
		if (tree->rchild != NULL) {
			putchar (',');
			binary_tree_print_tree (tree->rchild);
		}
		
		putchar (')');
	} else if (tree->rchild != NULL) {
		putchar ('(');
		
		binary_tree_print_tree (tree->lchild);
		if (tree->rchild != NULL) {
			putchar (',');
			binary_tree_print_tree (tree->rchild);
		}
		
		putchar (')');
	}
}

binary_tree_node *
binary_tree_rebuild_from_DLR_and_LDR (const data_type *DLR_sequence, const data_type *LDR_sequence, size_t length)
{
	if (length == 0)
		return NULL;
	else {
		binary_tree_node *tree = Malloc (sizeof (binary_tree_node));
		char D = DLR_sequence[0];
		tree->data = D;
		
		char *D_in_LDR_sequence = strchr (LDR_sequence, D);
		size_t llength = D_in_LDR_sequence - LDR_sequence;
		size_t rlength = length - llength - 1;
		
		tree->lchild = binary_tree_rebuild_from_DLR_and_LDR (&DLR_sequence[1], LDR_sequence, llength);
		tree->rchild = binary_tree_rebuild_from_DLR_and_LDR (&DLR_sequence[1 + llength], D_in_LDR_sequence + 1, rlength);
		return tree;
	}
}

void
binary_tree_traverse_level (binary_tree_node *tree,
                            void (*solve) (binary_tree_node *, void *),
                            void *arg)
{
	const int QUEUE_MAX_SIZE = 4096;
	binary_tree_node *queue[QUEUE_MAX_SIZE];
	int front, rear, tmp;
	front = rear = 0;
	
#define ENQUEUE(node)\
	queue[rear] = node, rear = (rear +1) % QUEUE_MAX_SIZE
	
#define DEQUEUE()                           \
	( tmp = front,                          \
	  front = (front +1) % QUEUE_MAX_SIZE,  \
	  queue[tmp]                            \
	)
#define IS_QUEUE_EMPTY()\
	( rear == front )
#define IS_QUEUE_FULL()\
	( (rear +1 ) % QUEUE_MAX_SIZE == front )
	
	
	ENQUEUE (tree);
	for (; !IS_QUEUE_EMPTY() ;) {
		binary_tree_node *curr = DEQUEUE();
		solve (curr, arg);
		if (curr->lchild != NULL)
			ENQUEUE (curr->lchild);
		if (curr->rchild != NULL)
			ENQUEUE (curr->rchild);
	}
	
#undef ENQUEUE
#undef DEQUEUE
#undef IS_QUEUE_EMPTY
#undef IS_QUEUE_FULL
}

void
binary_tree_traverse_level_const (const binary_tree_node *tree,
                                  void (*solve) (const binary_tree_node *, void *),
                                  void *arg)
{
	binary_tree_traverse_level (
	    (binary_tree_node *) tree,
	    (void (*) (binary_tree_node *, void *)) solve,
	    arg
	);
}

到了这里，关于二叉树C语言实现的文章就介绍完了。如果您还想了解更多内容，请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章，希望大家以后多多支持TOY模板网！