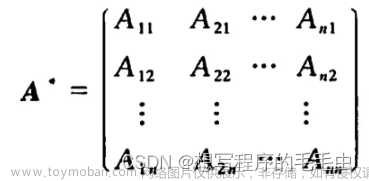
正定矩阵
在线性代数里,正定矩阵 (positive definite matrix) 有时会简称为正定阵。
广义定义:设M是n阶方阵,如果对任何非零向量z,都有
z
⃗
T
M
z
⃗
>
0
\vec{z}^TM\vec{z}>0
zTMz>0,则称M为正定矩阵。
狭义定义:一个n阶的实对称矩阵M是正定的的条件是当且仅当对于所有的非零实系数向量z,都有
z
⃗
T
M
z
⃗
>
0
\vec{z}^TM\vec{z}>0
zTMz>0。
- 若A是正定矩阵,则A的逆矩阵也是正定矩阵
- 若A是正定矩阵,则存在实可逆矩阵C使得 A = C T C A=C^TC A=CTC
矩阵的1/2次方
求矩阵A的1/2次方的前提是A为正定阵,这时A一定相似于主对角元素都为正数的对角阵,也就是说:存在可逆阵P,使得 P − 1 A P = Λ = d i a ( λ 1 , λ 2 , . . . , λ n ) P^{-1}AP=Λ=dia(λ_1,λ_2,...,λ_n) P−1AP=Λ=dia(λ1,λ2,...,λn)是对角阵。取 B = P ⋅ d i a g ( λ 1 , λ 2 , . . . , λ n ) P − 1 B=P·diag(\sqrt{λ_1},\sqrt{λ_2},...,\sqrt{λ_n})P^{-1} B=P⋅diag(λ1,λ2,...,λn)P−1,则 B 2 = A B^2=A B2=A,即 B = A 1 / 2 B=A^{1/2} B=A1/2。
矩阵的-1/2次方
同上,再对 B 1 / 2 B^{1/2} B1/2求逆。
拉普拉斯矩阵
拉普拉斯矩阵(Laplacian matrix) 也叫做导纳矩阵、基尔霍夫矩阵或离散拉普拉斯算子,主要应用在图论中,作为一个图的矩阵表示。
D:度矩阵,A:邻接矩阵,L:拉普拉斯矩阵
Combinatorial Laplacian:
L
=
D
−
A
L = D - A
L=D−A
图神经网络中常用的是正则化拉普拉斯矩阵 Symmetric normalized Laplacian:
L
=
D
−
1
/
2
L
D
1
/
2
L = D^{-1/2}LD^{1/2}
L=D−1/2LD1/2,这种代数形式和原本形式的区别是相当于做了一个归一化处理,具体到元素是(拉普拉斯矩阵的元素级的定义):
随机游走归一化拉普拉斯矩阵 Random walk normalized Laplacian
L
r
w
=
D
−
1
L
L^{rw}=D^{-1}L
Lrw=D−1L
为什么GCN要用拉普拉斯矩阵?
(1)拉普拉斯矩阵是对称矩阵,可以进行特征分解(谱分解);
(2)拉普拉斯矩阵只在中心顶点和一阶相连的顶点上(1-hop neighbor)有非0元素,其余之处均为0;
(3)通过拉普拉斯算子与拉普拉斯矩阵进行类比。文章来源:https://www.toymoban.com/news/detail-430210.html
- L是半正定矩阵(每个特征值 λ i ≥ 0 \lambda_i\geq0 λi≥0)
- L的每一行每一列的和为0
- L的最小特征值为0。
Reference
1.图神经网络——(2)图卷积神经网络
2. 拉普拉斯算子和拉普拉斯矩阵
3. 理解图的拉普拉斯矩阵
4. GNN入门之路: 01.图拉普拉斯矩阵的定义、推导、性质、应用
5. 图谱论学习—拉普拉斯矩阵背后的含义文章来源地址https://www.toymoban.com/news/detail-430210.html
到了这里,关于图拉普拉斯矩阵的文章就介绍完了。如果您还想了解更多内容,请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章,希望大家以后多多支持TOY模板网!