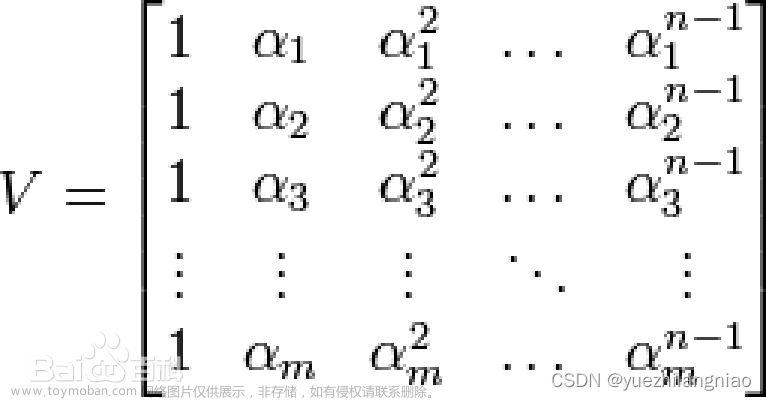
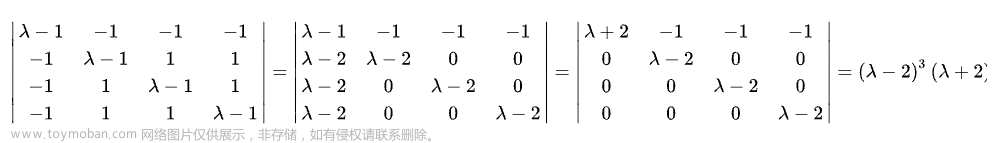先给结论:行列式是线性变化的伸缩因子
给定一个二阶行列式:
由行列式的计算方法可得:
矩阵可表示为二维空间上的两个向量和,这两个向量可以组成一个平行四边形。
下面证明
(平行四边形)
由:
三角形的面积公式:
得:
平行四边形的面积为:
由:
内积计算公式:
得
将代入平行四边形的面积公式得:
由此可以把二阶行列式理解为将面积为1的正方形伸缩变换为面积为的平行四边形(或者说D为矩阵对应的线性变换前后的面积比),正负号表示伸缩变换的方向。三阶行列式可理解为将体积为1的正方体伸缩变化为体积为的六面体。
各轴之间的顺序要求符合右手法则,即以右手握住Z轴,让右手的四指从X轴的正向以90度的直角转向Y轴的正向,这时大拇指所指的方向就是Z轴的正向。这样的三个坐标轴构成的坐标系称为右手空间直角坐标系.与之相对应的是左手空间直角坐标系.一般在数学中更常用右手空间直角坐标系 。
因此可证明以下结论:
1.行列式与其转置行列式相等,即。
由于转置只会改变图形位置,而不会改变面积,所以
2.对调两行(或列)行列式改变符号。
对调行或列表示将坐标轴对调,方向相反,所以会改变符号
3.行列式某行(或列)有公因子,可以提取到行列式的外面。
将某个向量扩大(或缩小)n倍,它与其它向量所组成的平行四边形的面积也会扩大(或缩小)n倍
4.若行列式某行或列元素全为0,则该行列式值为0。
一个向量为零,另一个向量无法围成平行四边形,因而不能算面积
5.若行列式某两行(或列)元素相同,则行列式值为0。
6.若行列式某两行(或列)元素对应成比例,则行列式值为0。
5和6都表示两个向量重合,其余向量无法围成封闭图形,因而不能算面积(或体积)
7.行列式某行(或列)的每个元素皆为两数之和,行列式可分解为两个行列式之和。
即:
可理解为将一次伸缩变化分解为两次伸缩变化。
8.行列式的某行(或某列)的倍数加到另一行(或列)行,列式不变。
由向量性质可证。文章来源:https://www.toymoban.com/news/detail-430279.html
文章来源地址https://www.toymoban.com/news/detail-430279.html
到了这里,关于讨论行列式的几何意义的文章就介绍完了。如果您还想了解更多内容,请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章,希望大家以后多多支持TOY模板网!