1 前言
1.1 奇异值分解
奇异值分解(Singular Value Decomposition,SVD)是一种重要的矩阵分解技术,它可以将一个矩阵分解为三个矩阵的乘积,分别为左奇异矩阵、奇异值矩阵和右奇异矩阵。SVD 的原理可以描述如下:
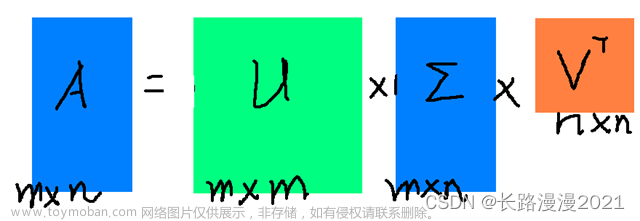
对于任意 m × n m \times n m×n 的矩阵 A A A,它的 SVD 分解为:
A = U $\sigma $ V T V^T VT
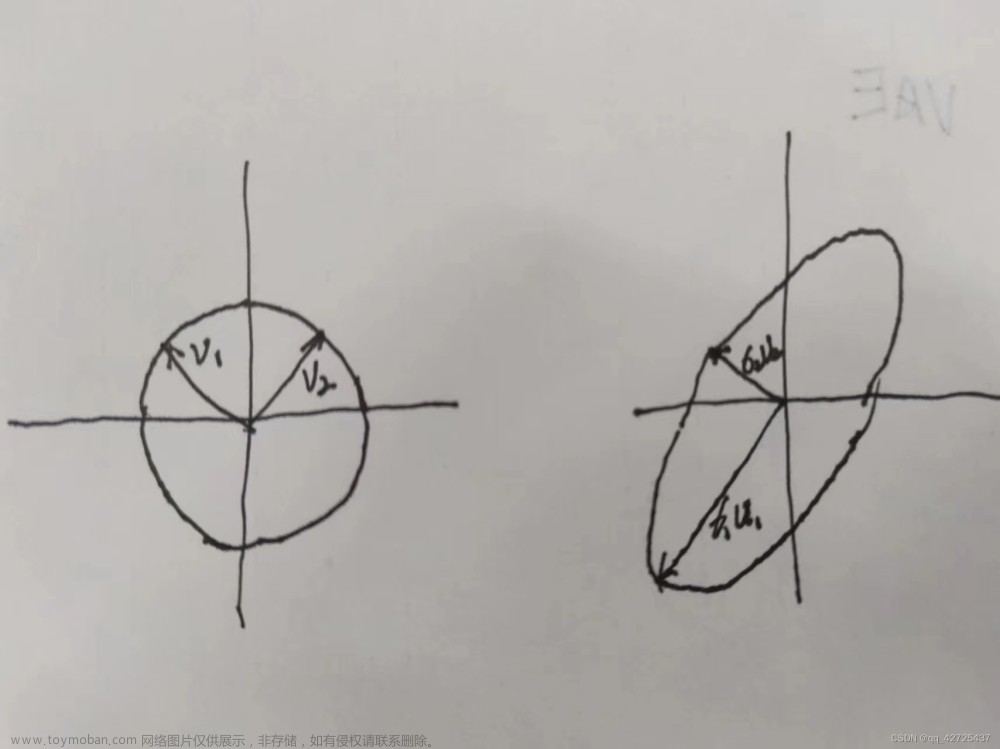
其中 A 是待分解的矩阵,U 是一个正交矩阵,$\sigma $ 是一个对角矩阵, V T V^T VT 是V 的转置。这个公式表示将 A 分解为三个矩阵的乘积,其中 U 和 V T V^T VT 表示矩阵 A 在左右两个方向上的正交基,$\sigma $ 表示每个基向量上的缩放因子,称为奇异值。
优点:
- SVD 可以处理非方阵和稠密矩阵,这是其他矩阵分解方法(如LU分解和QR分解)无法处理的情况。
- SVD 可以有效地进行降维,保留最重要的特征,从而可以在不影响模型性能的情况下减少特征数量。
- SVD 分解得到的三个矩阵可以分别表示原矩阵在行空间、列空间和主对角线方向的信息,有助于对矩阵的性质和特征进行分析。
缺点:
- SVD 运算时间复杂度较高,在处理大型矩阵时需要大量的计算资源。
- SVD 分解后得到的矩阵可能存在精度问题,特别是对于非常接近零的奇异值。
- SVD 分解的结果可能存在多解的情况,这需要根据实际问题和领域知识进行进一步的分析和处理。
1.2 奇异值分解的应用
奇异值分解是一种重要的矩阵分解方法,具有广泛的应用。以下是一些常见的应用场景:
-
数据降维:SVD 可以对高维数据进行降维处理,减少数据的冗余信息和噪声,提取最重要的特征。这种方法在数据挖掘、机器学习等领域广泛应用。
-
图像处理:SVD 可以将图像矩阵分解成三个矩阵,其中一个矩阵可以表示图像的主要特征,从而可以实现图像压缩、降噪等处理。此外,SVD 在图像水印、图像检索等方面也有重要应用。
-
推荐系统:SVD 可以将用户-物品评分矩阵分解成三个矩阵,其中一个矩阵可以表示用户的偏好特征,另一个矩阵可以表示物品的属性特征。这种方法在推荐系统中广泛应用,例如Netflix竞赛中的著名算法。
-
自然语言处理:SVD 可以对文本矩阵进行分解,提取文本的重要主题和特征,用于文本分类、文本聚类、文本推荐等任务。
-
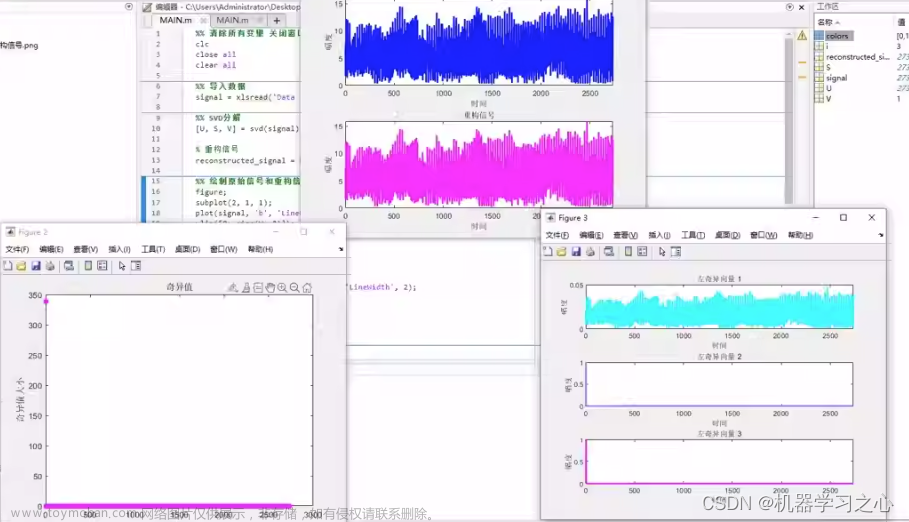
信号处理:SVD 可以将信号分解成一系列奇异值,这些奇异值表示信号的能量和频率分布等信息,从而可以实现信号分离、降噪、压缩等处理。
2 简单计算SVD
2.1 NumPy 计算 SVD
在numpy.linalg中使用 SVD 获得完整的矩阵 U、S 和 V。请注意,S 是一个对角矩阵,这意味着它的大部分条目都是零。这称为稀疏矩阵。为了节省空间,S 返回为奇异值的一维数组而不是完整的二维矩阵
import numpy as np
from numpy.linalg import svd
# 将矩阵定义为二维numpy数组
A = np.array([[4, 0], [3, -5]])
U, S, VT = svd(A)
print("Left Singular Vectors:")
print(U)
print("Singular Values:")
print(np.diag(S))
print("Right Singular Vectors:")
print(VT)
print(U @ np.diag(S) @ VT)

2.2 scikit-learn 计算截断 SVD
一般情况下用sklearn.decomposition中的TruncatedSVD修剪我们的矩阵。可以将输出中所需的特征数指定为n_components参数。n_components 应严格小于输入矩阵中的特征数:
import numpy as np
from sklearn.decomposition import TruncatedSVD
A = np.array([[-1, 2, 0], [2, 0, -2], [0, -2, 1]])
print("Original Matrix:")
print(A)
svd = TruncatedSVD(n_components = 2)
A_transf = svd.fit_transform(A)
print("Singular values:")
print(svd.singular_values_)
print("Transformed Matrix after reducing to 2 features:")
print(A_transf)

2.3 scikit-learn 计算随机 SVD
随机 SVD 给出与截断 SVD 相同的结果,并且计算时间更快。截断 SVD 使用精确求解器 ARPACK,而随机 SVD 使用近似技术。
import numpy as np
from sklearn.utils.extmath import randomized_svd
A = np.array([[-1, 2, 0], [2, 0, -2], [0, -2, 1]])
u, s, vt = randomized_svd(A, n_components = 2)
print("Left Singular Vectors:")
print(u)
print("Singular Values:")
print(np.diag(s))
print("Right Singular Vectors:")
print(vt)

3 demo数据演示
3.1 导入函数
加载cv2需要下载一下,在shell中下载用以下命令,在jupyter中运行记得加!,这里为了齐全下载了opencv-contrib-python
pip install opencv-python (如果只用主模块,使用这个命令安装)
pip install opencv-contrib-python (如果需要用主模块和contrib模块,使用这个命令安装)
# !pip install opencv-contrib-python
import numpy as np
import matplotlib.pyplot as plt
import cv2
3.2 导入数据
构建一个简单矩阵
A = np.ones((6, 6))
A[:,:2] = A[:,:2]*2
A[:,2:4] = A[:,2:4]*3
A[:,4:] = A[:,4:]*4
print(A)
# 定义颜色
our_map = 'hot'
#our_map = 'gray'
# 构建完整矩阵
U, S, VT = np.linalg.svd(A)
S = np.diag(S)
3.3 计算SVD
写一个一个构建绘制矩阵函数的def,类似于R的function,定义为draw_svd
def draw_svd(A,U, S, VT, our_map):
plt.subplot(221 )
plt.title('Original matrix')
plt.imshow(A, cmap =our_map)
plt.axis('off')
plt.subplot(222)
plt.title('U matrix')
plt.imshow(U, cmap =our_map)
plt.axis('off')
plt.subplot(223)
plt.title('Sigma matrix')
plt.imshow(S, cmap =our_map)
plt.axis('off')
plt.subplot(224)
plt.title('V matrix')
plt.imshow(VT, cmap =our_map)
plt.axis('off')
如果对角线 sigma 值太小,出于数值/美学目的,我们将删除相应的非常小的 (u ), (v ) 元素。例如,如果一个奇异值是 1e-08 它不会影响重建,所以我们将这些小值设置为零:
def truncate_u_v(S, U, VT):
threshold = 0.001
s = np.diag(S)
index = s < threshold
U[:,index] = 0
VT[index,:]=0
return U, VT
U, VT = truncate_u_v(S, U, VT)
draw_svd(A, U, S, VT, our_map)

这里用秩r近似值(这里r = 1),也称rank-1 近似计算有多少个求和项:
r = 1
A0_r = np.matmul(U[:,:r] , S[:r,:r])
A0_r = np.matmul (A0_r , VT[:r,:])
plt.imshow(A0_r, cmap = our_map)
plt.axis('off')

对于这个例子,我们之前已经看到标志可以表示为 rank-1 近似值。在 ($\sigma $) 矩阵中,第一个上部元素是唯一的非零元素。此外,请注意,矩阵 (U ) 和 (V ) 被归一化,因此它们的 L2 范数等于 1。(V ) 矩阵有一行,其元素决定了不同的颜色值。
求解前面部分的 ($2\times2 $) 矩阵的数值示例。稍后将 Python 获得的值与我们已经计算出的值进行比较:
A = [[1, 0], [1, 1]]
U, S, VT = np.linalg.svd(A)
S = np.diag(S)
print(f"U {U}\nS {S}\nVT {VT}")

4 讨论
SVD 正在将我们的矩阵 $(A ) 分解为一组向量 分解为一组向量 分解为一组向量 (v $) 和 $(u $),以及一个对角矩阵。将有用于乘法的列向量、行向量和标量。这实际上是奇异值分解,将矩阵分解为项:
如果我们有一个 rank = ($2 $),我们可以将矩阵分解为:
u 1 v 1 T + u 2 v 2 T u_{1}v_{1}^{T}+u_{2}v_{2}^{T} u1v1T+u2v2T
如果 rank = ($1 $),结果应该是这样的:
u 1 v 1 T u_{1}v_{1}^{T} u1v1T
稍微复杂一点的分解是添加标量 (($\sigma $) – σ \sigma σ),这将存储在对角矩阵中。我们对 rank-($2 $) 矩阵 ($2 $) 的基本分解:
A = σ 1 u 1 v 1 T + σ 2 u 2 v 2 T A= \sigma _{1} u_{1}v_{1}^{T}+\sigma _{2} u_{2}v_{2}^{T} A=σ1u1v1T+σ2u2v2T
这里很明显的一件事是,实际上我们可以将这些 σ \sigma σ 值视为加权系数。稍后,我们将它们存储在对角矩阵中。
SVD最常见的应用还是关于图像的,和笔者研究方向数据分析重合度不算高,后者只需要针对数据进行简单的降维即可,但对于图像压缩,图像恢复特征量,谱聚类,视频背景去除等对于我这个学生物统计的真的裂开,文章来源:https://www.toymoban.com/news/detail-430441.html
SVD这一部分实在难啃,建议阅读原文细品:文章来源地址https://www.toymoban.com/news/detail-430441.html
- https://datahacker.rs/009-the-singular-value-decompositionsvd-illustrated-in-python/
- https://scicoding.com/how-to-calculate-singular-value-decomposition-svd-in-python/
到了这里,关于机器学习实战:Python基于SVD奇异值分解进行矩阵分解(八)的文章就介绍完了。如果您还想了解更多内容,请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章,希望大家以后多多支持TOY模板网!