高级数据结构 Trie树(字典树）

高级数据结构 Trie树（字典树）

（Trie Tree）字典树_Rkun18的博客-CSDN博客

字典树节点表示

#define TRIE_MAX_CHAR_NUM 26
//这里你可以自由设置 根据不同需求设置 如果有大小或者其他符号你就需要增大这个数字

struct TrieNode{
    TrieNode *child[TRIE_MAX_CHAR_NUM];
    bool isEnd;
    TrieNode():isEnd(false){
        for (int i = 0; i < TRIE_MAX_CHAR_NUM; ++i) {
            child[i]=0;
        }
    }
};

构造字典树

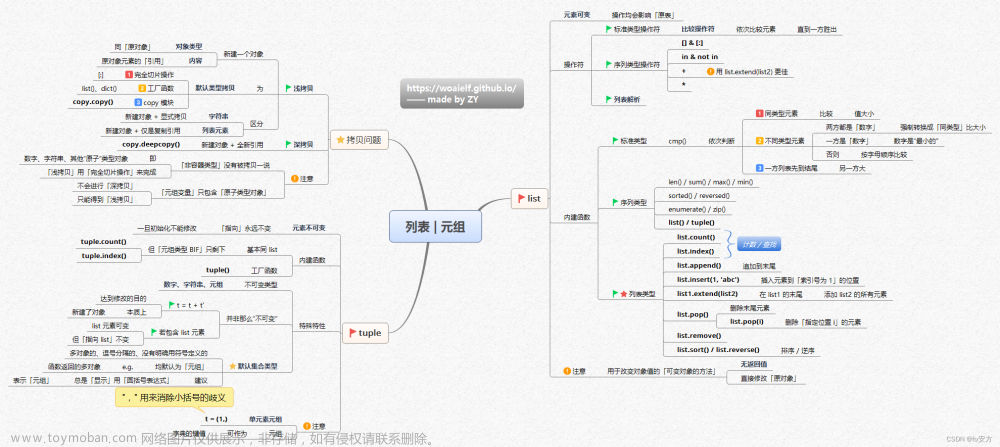
这里使用维基百科里的一幅图举例，由于只是举例，使用较小的26个字母，把大小写统一规定成小写，图里’A’变成’a’，方便构造树

int main() {
    TrieNode root;//根
    TrieNode n1,n2,n3;//树的第一层
    root.child['t'-'a']=&n1;
    root.child['a'-'a']=&n2;
    root.child['i'-'a']=&n3;
    n2.isEnd= true;//单个字符串走到末尾
    n3.isEnd= true;
    TrieNode n4,n5,n6;//第二层
    n1.child['o'-'a']=&n4;
    n4.isEnd= true;
    n1.child['e'-'a']=&n5;
    n3.child['n'-'a']=&n6;
    n6.isEnd= true;
    TrieNode n7,n8,n9,n10;//最后一层
    n5.child['a'-'a']=&n7;
    n7.isEnd= true;
    n5.child['d'-'a']=&n8;
    n8.isEnd= true;
    n5.child['n'-'a']=&n9;
    n9.isEnd= true;
    n6.child['n'-'a']=&n10;
    n10.isEnd= true;
    preorder(&root,0);//先序遍历







    return 0;
}

先序遍历

void preorder(TrieNode *node,int layer){
    for (int i = 0; i < TRIE_MAX_CHAR_NUM; ++i) {
        if(node->child[i]){
            for (int j = 0; j <layer ; ++j) {
                printf("-");
            }
            printf("%c",i+'a');
            if(node->child[i]->isEnd){
                printf("[done]");
            }
            printf("\n");
            preorder(node->child[i],layer+1);
        }


    }

}

main方法运行：

a[done]  
i[done]  
-n[done] 
--n[done]
t        
-e       
--a[done]
--d[done]
--n[done]
-o[done] 

Trie获取所有单词

• 深度搜索trie树，对于正在搜索的节点node

• 遍历该节点的所有孩子指针child[i]，如果指针不为空，将child[i]对应字符放入栈里

• 如果孩子指针isEnd为真,从栈底到栈顶对栈遍历，生成字符串，将它保存至结果数组中去

• 深度搜索child[i]

• 弹出栈顶字符

void get_all_word(TrieNode *node, string &word, vector<string> &wordList) {
    for (int i = 0; i < TRIE_MAX_CHAR_NUM; ++i) {
        if (node->child[i]) {
            word.push_back((char) i + 'a');//字符入栈
            if (node->child[i]->isEnd) {
                wordList.push_back(word);
            }
            get_all_word(node->child[i], word, wordList);
            word.erase(word.length() - 1, 1);//弹出栈顶字符

        }

    }
}

int main() {
    TrieNode root;//根
    TrieNode n1, n2, n3;//树的第一层
    root.child['t' - 'a'] = &n1;
    root.child['a' - 'a'] = &n2;
    root.child['i' - 'a'] = &n3;
    n2.isEnd = true;//单个字符串走到末尾
    n3.isEnd = true;
    TrieNode n4, n5, n6;//第二层
    n1.child['o' - 'a'] = &n4;
    n4.isEnd = true;
    n1.child['e' - 'a'] = &n5;
    n3.child['n' - 'a'] = &n6;
    n6.isEnd = true;
    TrieNode n7, n8, n9, n10;//最后一层
    n5.child['a' - 'a'] = &n7;
    n7.isEnd = true;
    n5.child['d' - 'a'] = &n8;
    n8.isEnd = true;
    n5.child['n' - 'a'] = &n9;
    n9.isEnd = true;
    n6.child['n' - 'a'] = &n10;
    n10.isEnd = true;
    vector<string> wordList;
    string word = "";
    get_all_word(&root, word, wordList);
    for (int i = 0; i < wordList.size(); ++i) {
        cout << wordList[i] << endl;
    }


    return 0;
}

a
i  
in 
inn
tea
ted
ten
to 

整体功能

class Trie{
public:
    Trie(){
    }
    ~Trie(){
        for (int i = 0; i <_node_vec.size() ; ++i) {
             delete _node_vec[i];
        }
    } //插入
    void insert(const char *word){

    }//查找
    bool search(const char *word){

    }//是否有以某个字符串为前缀的
    bool startsWith(const char *prefix){

    }
    TrieNode *root(){
        return &_root;
    }


private:
    TrieNode *newNode(){
        TrieNode *node=new TrieNode();
        _node_vec.push_back(node);
        return node;

    }
    vector<TrieNode *>_node_vec;
    TrieNode _root;
};

插入

• 使用指针ptr指向root

• 逐个遍历待插入字符串中的各个字符

• 计算下标pos=’正在遍历字符’-‘a’

• 如果ptr指向第pos孩子为假:

• 创建该节点第pos个孩子

• ptr指向该节点的第pos个孩子

• 标记ptr指向节点的isEnd为true

   void insert(const char *word){
        TrieNode *ptr=&_root;
        while (*word){
            int pos=*word-'a';
            if(!ptr->child[pos]){
                ptr->child[pos]=newNode();
                
            }
            ptr=ptr->child[pos];
            word++;
            
        }
        ptr->isEnd= true;

    }

搜索

• 使用ptr指针指向root

• 逐个遍历带搜索字符各个字符

• 计算下标pos=’正在遍历字符’-‘a’

• 如果ptr指向节点第pos个孩子为假：返回假

• ptr指向第pos个孩子

• 返回ptr指向节点的isEnd

 bool search(const char *word){
        TrieNode *ptr=&_root;
        while (*word){
            int pos=*word-'a';
            if(!ptr->child[pos]){
                return false;
            }
            ptr=ptr->child[pos];
            word++;
        }
        return ptr->isEnd;

    }

判断前缀是否存在

bool startsWith(const char *prefix){
        TrieNode *ptr=&_root;
        while (*prefix){
            int pos=*prefix-'a';
            if(!ptr->child[pos]){
                return false;
            }
            ptr=ptr->child[pos];
            prefix++;
        }
        return true;

    }

前缀树代码

class Trie{
public:
    Trie(){
    }
    ~Trie(){
        for (int i = 0; i <_node_vec.size() ; ++i) {
             delete _node_vec[i];
        }
    }
    void insert(const char *word){
        TrieNode *ptr=&_root;
        while (*word){
            int pos=*word-'a';
            if(!ptr->child[pos]){
                ptr->child[pos]=newNode();

            }
            ptr=ptr->child[pos];
            word++;

        }
        ptr->isEnd= true;

    }
    bool search(const char *word){
        TrieNode *ptr=&_root;
        while (*word){
            int pos=*word-'a';
            if(!ptr->child[pos]){
                return false;
            }
            ptr=ptr->child[pos];
            word++;
        }
        return ptr->isEnd;

    }
    bool startsWith(const char *prefix){
        TrieNode *ptr=&_root;
        while (*prefix){
            int pos=*prefix-'a';
            if(!ptr->child[pos]){
                return false;
            }
            ptr=ptr->child[pos];
            prefix++;
        }
        return true;

    }
    TrieNode *root(){
        return &_root;
    }


private:
    TrieNode *newNode(){
        TrieNode *node=new TrieNode();
        _node_vec.push_back(node);
        return node;

    }
    vector<TrieNode *>_node_vec;
    TrieNode _root;
};

测试

int main() {
    Trie trie;
    trie.insert("hello");
    trie.insert("echo");
    trie.insert("eleven");
    trie.insert("how");
    cout<<"preorder_trie:"<<endl;
    preorder(trie.root(),0);
    vector<string>ls;
    string word;
    cout<<"All words:"<<endl;
    get_all_word(trie.root(),word,ls);
    for (int i = 0; i < ls.size(); ++i){
        cout<<ls[i]<<endl;
    }
    cout<<"Search:"<<endl;
    printf("hello :%d\n",trie.search("hello"));
    printf("hel :%d\n",trie.search("hel"));
    cout<<"StartsWith:"<<endl;
    printf("hello :%d\n",trie.startsWith("hello"));
    printf("hel :%d\n",trie.startsWith("hel"));




    return 0;
}

e             
-c            
--h           
---o[done]    
-l            
--e           
---v          
----e         
-----n[done]  
h             
-e            
--l           
---l          
----o[done]   
-o            
--w[done]     
All words:    
echo          
eleven        
hello         
how           
Search:       
hello :1      
hel :0        
StartsWith:
hello :1
hel :1

208. 实现 Trie (前缀树)

力扣

直接使用Trie类，改个名，调用方法把string通过c_str()，变成字符数组

#define TRIE_MAX_CHAR_NUM 26
//这里你可以自由设置 根据不同需求设置 如果有大小或者其他符号你就需要增大这个数字

struct TrieNode{
    TrieNode *child[TRIE_MAX_CHAR_NUM];
    bool isEnd;
    TrieNode():isEnd(false){
        for (int i = 0; i < TRIE_MAX_CHAR_NUM; ++i) {
            child[i]=0;
        }
    }
};


using namespace std;
class Trie1{
public:
    Trie1(){
    }
    ~Trie1(){
        for (int i = 0; i <_node_vec.size() ; ++i) {
             delete _node_vec[i];
        }
    }
    void insert(const char *word){
        TrieNode *ptr=&_root;
        while (*word){
            int pos=*word-'a';
            if(!ptr->child[pos]){
                ptr->child[pos]=newNode();

            }
            ptr=ptr->child[pos];
            word++;

        }
        ptr->isEnd= true;

    }
    bool search(const char *word){
        TrieNode *ptr=&_root;
        while (*word){
            int pos=*word-'a';
            if(!ptr->child[pos]){
                return false;
            }
            ptr=ptr->child[pos];
            word++;
        }
        return ptr->isEnd;

    }
    bool startsWith(const char *prefix){
        TrieNode *ptr=&_root;
        while (*prefix){
            int pos=*prefix-'a';
            if(!ptr->child[pos]){
                return false;
            }
            ptr=ptr->child[pos];
            prefix++;
        }
        return true;

    }
    TrieNode *root(){
        return &_root;
    }


private:
    TrieNode *newNode(){
        TrieNode *node=new TrieNode();
        _node_vec.push_back(node);
        return node;

    }
    vector<TrieNode *>_node_vec;
    TrieNode _root;
};







class Trie {
public:
    Trie() {

    }
    
    void insert(string word) {
       trie.insert(word.c_str());
    }
    
    bool search(string word) {
       return trie.search(word.c_str());
    }
    
    bool startsWith(string prefix) {
        return trie.startsWith(prefix.c_str());
    }
private:
   Trie1 trie;
};

/**
 * Your Trie object will be instantiated and called as such:
 * Trie* obj = new Trie();
 * obj->insert(word);
 * bool param_2 = obj->search(word);
 * bool param_3 = obj->startsWith(prefix);
 */

211. 添加与搜索单词 - 数据结构设计

力扣

这里考虑搜索遇到’.'如何

• 当遍历到单词结束时

• 如果node指向的节点标记为单词的结尾(isEnd==true)返回真，否则返回假

• 如果word遇到’.’

• 遍历所有node的孩子指针，继续递归搜索，单词指针向前移动一个位置，如果递归搜索结果为真，返回真

• 如果不是’.’

• 计算孩子位置pos,pos指向当前孩子为真，继续深搜，指针向前移动一个位置，如果搜索结果为真，返回真

下面来改写这个search方法文章来源地址https://www.toymoban.com/news/detail-430451.html

#define TRIE_MAX_CHAR_NUM 26
//这里你可以自由设置 根据不同需求设置 如果有大小或者其他符号你就需要增大这个数字

struct TrieNode {
    TrieNode *child[TRIE_MAX_CHAR_NUM];
    bool isEnd;

    TrieNode() : isEnd(false) {
        for (int i = 0; i < TRIE_MAX_CHAR_NUM; ++i) {
            child[i] = 0;
        }
    }
};




class Trie {
public:
    Trie() {
    }

    ~Trie() {
        for (int i = 0; i < _node_vec.size(); ++i) {
            delete _node_vec[i];
        }
    }

    void insert(const char *word) {
        TrieNode *ptr = &_root;
        while (*word) {
            int pos = *word - 'a';
            if (!ptr->child[pos]) {
                ptr->child[pos] = newNode();

            }
            ptr = ptr->child[pos];
            word++;

        }
        ptr->isEnd = true;

    }

    bool search_tire(TrieNode *node, const char *word) {
        if (*word == '\0') {
            if (node->isEnd) {
                return true;
            }
            return false;
        }
        if (*word == '.') {
            for (int i = 0; i < TRIE_MAX_CHAR_NUM; ++i) {
                if (node->child[i] && search_tire(node->child[i], word + 1)) {
                    return true;
                }

            }
        } else {
            int pos = *word - 'a';
            if (node->child[pos] && search_tire(node->child[pos], word + 1)) {
                return true;
            }
        }
        return false;


    }

    bool startsWith(const char *prefix) {
        TrieNode *ptr = &_root;
        while (*prefix) {
            int pos = *prefix - 'a';
            if (!ptr->child[pos]) {
                return false;
            }
            ptr = ptr->child[pos];
            prefix++;
        }
        return true;

    }

    TrieNode *root() {
        return &_root;
    }


private:
    TrieNode *newNode() {
        TrieNode *node = new TrieNode();
        _node_vec.push_back(node);
        return node;

    }

    vector<TrieNode *> _node_vec;
    TrieNode _root;
};



class WordDictionary {
public:
    WordDictionary() {

    }
    
    void addWord(string word) {
        trie.insert(word.c_str());


    }
    
    bool search(string word) {
       return trie.search_tire(trie.root(),word.c_str());
    }
private:
      Trie trie;
};

/**
 * Your WordDictionary object will be instantiated and called as such:
 * WordDictionary* obj = new WordDictionary();
 * obj->addWord(word);
 * bool param_2 = obj->search(word);
 */

到了这里，关于高级数据结构 Trie树(字典树）的文章就介绍完了。如果您还想了解更多内容，请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章，希望大家以后多多支持TOY模板网！