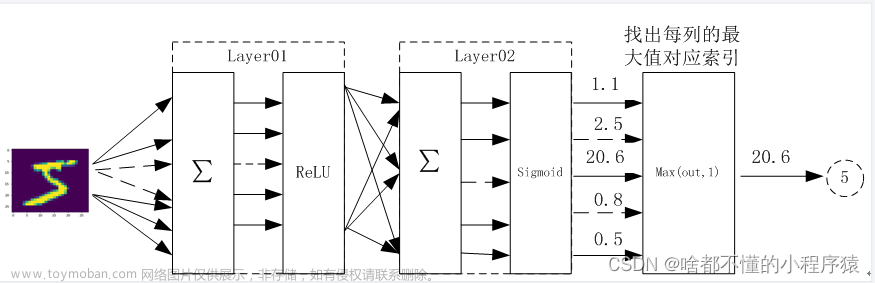
手写数字识别神经网络
基本原理
图像本质上被认为是一个矩阵,每个像素点都是一个对应的像素值,相当于在多维数据上进行相关的归类或者其他操作。
线性函数
线性函数的一个从输入到输出的映射,用于给目标一个每个类别对应的得分。
图像 ( 32 ∗ 32 ∗ 3 ) → f ( x , W ) Y 图像(32*32*3) \stackrel{f(x,W)}{\rightarrow} Y 图像(32∗32∗3)→f(x,W)Y
其中 x x x为3072维的一个向量,
W W W为parameters
Y Y Y为图像对应每个类别对应的得分
f ( x , W ) = W x ( + b ) f(x,W)=Wx(+b) f(x,W)=Wx(+b)
其中 f ( x , W ) f(x,W) f(x,W)是10*1维度
W W W是10*3072维度
x x x是3072*1维度
b b b是10*1维度

损失函数
得到了输入图像和分类目标直接对应的每类得分,我们如何去分析衡量分类的结果?我们可以使用损失函数去明确当前模型的效果是好是坏。
损失函数可以表示为:
损失函数 = 数据损失 + 正则化惩罚项
L
=
1
N
∑
i
=
1
N
m
a
x
(
0
,
f
(
x
i
;
W
)
j
−
f
(
x
i
;
W
)
y
i
+
1
)
+
λ
R
(
W
)
L=\frac{1}{N} \sum\limits\limits_{i=1}^{N}max(0,f(x_i;W)_j-f(x_i;W)_{y_i}+1)+\lambda R(W)
L=N1i=1∑Nmax(0,f(xi;W)j−f(xi;W)yi+1)+λR(W)
其中R(W)项为正则化惩罚项,用于减少模型复杂度,防止过拟合,其中其
λ
\lambda
λ参数越大惩罚力度越大,也就是我们约不希望他过拟合。
R
(
W
)
=
∑
k
∑
l
W
k
,
l
2
R(W)=\sum\limits_{k}\sum\limits_{l}W _{k,l}^{2}
R(W)=k∑l∑Wk,l2
其中一个常用损失函数为
L
i
=
∑
j
≠
y
i
m
a
x
(
0
,
s
j
−
s
y
i
+
1
)
L_{i}=\sum\limits_{j \neq y_i}max(0,s_j-s_{y_i}+1)
Li=j=yi∑max(0,sj−syi+1)
在某次训练过程中,几个任务图像的线性函数输出结果如下所示:

我们分别计算其损失函数:
= m a x ( 0 , 5.1 − 3.2 + 1 ) + m a x ( 0 , − 1.7 − 3.2 + 1 ) = m a x ( 0 , 2.9 ) + m a x ( 0 , − 0.39 ) = 2.9 \begin{aligned} &=max(0,5.1-3.2+1)+max(0,-1.7-3.2+1) \\ &=max(0,2.9)+max(0,-0.39)\\ &=2.9 \end{aligned} =max(0,5.1−3.2+1)+max(0,−1.7−3.2+1)=max(0,2.9)+max(0,−0.39)=2.9
= m a x ( 0 , 1.3 − 4.9 + 1 ) + m a x ( 0 , 2.0 − 4.9 + 1 ) = m a x ( 0 , − 2.6 ) + m a x ( 0 , − 1.9 ) = 0 \begin{aligned} &=max(0,1.3-4.9+1)+max(0,2.0-4.9+1) \\ &=max(0,-2.6)+max(0,-1.9)\\ &=0 \end{aligned} =max(0,1.3−4.9+1)+max(0,2.0−4.9+1)=max(0,−2.6)+max(0,−1.9)=0
=
m
a
x
(
0
,
2.2
−
(
−
3.1
)
+
1
)
+
m
a
x
(
0
,
2.5
−
(
−
3.1
)
+
1
)
=
m
a
x
(
0
,
5.3
)
+
m
a
x
(
0
,
5.6
)
=
10.9
\begin{aligned} &=max(0,2.2-(-3.1)+1)+max(0,2.5-(-3.1)+1) \\ &=max(0,5.3)+max(0,5.6)\\ &=10.9 \end{aligned}
=max(0,2.2−(−3.1)+1)+max(0,2.5−(−3.1)+1)=max(0,5.3)+max(0,5.6)=10.9
我们可以根据本轮损失函数的计算去判断当前分类效果的好坏。
所以损失值我们通过一下流程进行得到:

前向传播(梯度下降)
我们知道了当前的模型的性能效果,那么肯定要对模型进行更新来达到一个更佳的状态
暂略
整体架构

数据模块
我们可以使用现成的torch中帮忙封装的MNIST数据,通过datasets包可以直接进行下载,并且使用dataloader加载数据。
def data_pre():
train_data=torchvision.datasets.MNIST(
root='MNIST',
train=True,
transform=torchvision.transforms.ToTensor(),
download=True
)
test_data=torchvision.datasets.MNIST(
root='MNIST',
train=False,
transform=torchvision.transforms.ToTensor(),
download=True
)
train_load=DataLoader(dataset=train_data,batch_size=100,shuffle=True)
test_load=DataLoader(dataset=test_data,batch_size=100,shuffle=True)
return train_data, test_data
torchvision.datasets.MNIST参数含义
- root:
存放训练和测试数据的文件根目录
- train:(数据类型bool)
如果为True则从training创建数据集,否则从test.pt创建数据集
- download:(数据类型bool)
如果为ture则从网络上下载数据集并放在根目录下,如果数据已经存在不会进行重复下载
- transform:(数据类型callable)
对数据内容进行转换处理的函数,具体见torchvision.transforms中的参数设置,此处为将PIL文件转换成tensor的数据格式
DataLoader参数含义
- dataset:(数据类型 dataset)
PyTorch中的数据集类型。
- batch_size:(数据类型 int)
每次输入数据的行数,默认为1。PyTorch训练模型时调用数据不是一个一个进行的,而是一批一批输入用于提升效率。这里就是定义每次喂给神经网络多少行数据,如果设置成1,那就是一行一行进行(个人偏好,PyTorch默认设置是1)。
- shuffle:(数据类型 bool)
洗牌。默认设置为False。在每次迭代训练时是否将数据洗牌,默认设置是False。将输入数据的顺序打乱,是为了使数据更有独立性,但如果数据是有序列特征的,就不要设置成True了。
神经网络框架
class neuralnet():
def __init__(self, input_nodes, hidden_nodes, output_nodes, learning_rate):
self.inodes = input_nodes # 输入层节点设定
self.hnodes = hidden_nodes # 隐藏层节点设定
self.onodes = output_nodes # 输出层节点设定
self.lr = learning_rate # 学习率设定
# 初始化w_ih
# 输入层与隐藏层之间的连接参数
self.wih = (np.random.normal(0.0, pow(self.hnodes, -0.5),\
(self.hnodes, self.inodes)))
# 隐藏层与输出层之间的连接参数
self.who = (np.random.normal(0.0, pow(self.onodes,-0.5),\
(self.onodes,self.hnodes)))
# 激活函数,返回sigmoid函数
self.activation_function = lambda x:spe.expit(x)
def train(self, inputs_list, targets_list):
# 输入进来的二维图像数据
inputs = np.array(inputs_list, ndmin=2).T
# 隐藏层计算
hidden_inputs = np.dot(self.wih, inputs)
# 隐藏层的输出经过sigmoid函数处理
hidden_outputs = self.activation_function(hidden_inputs)
# 输出层计算
final_inputs = np.dot(self.who, hidden_outputs)
# 输出经过sigmoid函数处理
final_outputs = self.activation_function(final_inputs)
# 取得对应的标签
targets = np.array(targets_list, ndmin=2).T
# 计算数据预测误差,将其用于向前反馈
output_errors = targets - final_outputs
# 根据公式计算得到反向传播参数
hidden_errors = np.dot(self.who.T,output_errors)
# 根据反馈参数去修改两个权重
self.who += self.lr * np.dot((output_errors * final_outputs *(1.0 - final_outputs)),np.transpose(hidden_outputs))
self.wih += self.lr * np.dot((hidden_errors * hidden_outputs * (1.0-hidden_outputs)), np.transpose(inputs))
def query(self, inputs_list):
# 输入进来的二维图像数据
inputs = np.array(inputs_list, ndmin=2).T
# 隐藏层计算
hidden_inputs = np.dot(self.wih, inputs)
# 隐藏层的输出经过sigmoid函数处理
hidden_outputs = self.activation_function(hidden_inputs)
# 输出层计算
final_inputs = np.dot(self.who, hidden_outputs)
# 输出经过sigmoid函数处理
final_outputs = self.activation_function(final_inputs)
return final_outputs
参考
(29条消息) [ PyTorch ] torch.utils.data.DataLoader 中文使用手册_江南蜡笔小新的博客-CSDN博客
(29条消息) 「学习笔记」torchvision.datasets.MNIST 参数解读/中文使用手册_江南蜡笔小新的博客-CSDN博客_torchvision.datasets.mnist
Python scipy.special.expit用法及代码示例 - 纯净天空 (vimsky.com)
002-深度学习数学基础(神经网络、梯度下降、损失函数) - 小小猿笔记 - 博客园 (cnblogs.com)文章来源:https://www.toymoban.com/news/detail-430453.html
TensorBoard的最全使用教程:看这篇就够了 - 腾讯云开发者社区-腾讯云 (tencent.com)文章来源地址https://www.toymoban.com/news/detail-430453.html
到了这里,关于神经网络基础-手写数字识别的文章就介绍完了。如果您还想了解更多内容,请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章,希望大家以后多多支持TOY模板网!