引言
重新复习了一下机器人学DH参数，并且利用matlab符号运算进行了推导，验证了公式。
1.DH参数原理
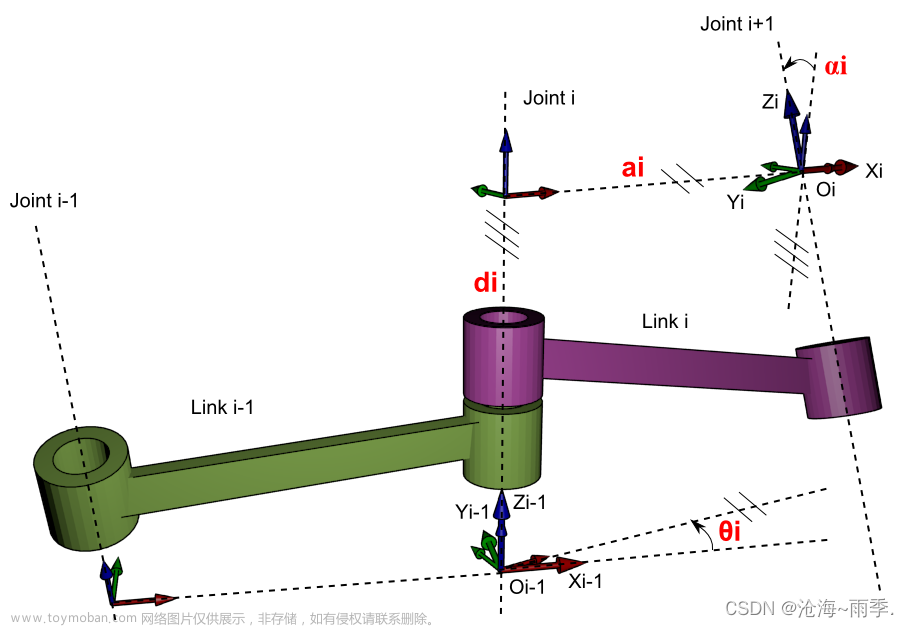
图中的坐标系定义：
- 坐标系 i {i} i的 z z z轴 z i z_i zi和关节轴线 i i i共线，指向任意规定。
- 坐标系 i {i} i的 x x x轴 x i x_i xi和 a i a_i ai重合，由关节 i i i指向关节 i + 1 i+1 i+1，当 a i = 0 a_i=0 ai=0，取 x i = ± z i + 1 × z i x_i=±z_{i+1}\times z_i xi=±zi+1×zi。
- 坐标系 i {i} i的 y y y轴 y i y_i yi按右手法则规定。
- 坐标系 i {i} i的原点 o i o_i oi取在 x i x_i xi和 z i z_i zi的交点上；当 z i z_i zi和 z i + z_{i+} zi+相交时，原点取再两轴交点上，当 z i z_i zi和 z i + z_{i+} zi+平行时，原点取在使 d i + 1 = 0 d_{i+1}=0 di+1=0的地方。
利用连杆坐标系定义相应的连杆参数：
- a i a_i ai=从 z i z_i zi到 z i + 1 z_{i+1} zi+1沿 x i x_i xi测量的距离（公垂线长度）
- α i \alpha_i αi=从 z i z_i zi到 z i + 1 z_{i+1} zi+1沿 x i x_i xi旋转的角度
- d i d_i di=从 x i − 1 x_{i-1} xi−1到 x i x_{i} xi沿 z i z_i zi测量的距离
- θ i \theta_i θi=从 x i − 1 x_{i-1} xi−1到 x i x_{i} xi沿 z i z_i zi旋转的角度
坐标系 { i } \{i\} {i}相对坐标系 { i − 1 } \{i-1\} {i−1}的变换矩阵 i − 1 T i {}^{i-1}T_{i} i−1Ti可以看作四个子变换矩阵的乘积：
- 绕
x
i
−
1
x_{i-1}
xi−1轴转
α
i
−
1
\alpha_{i-1}
αi−1角
R o t x ( α i − 1 ) = [ 1 0 0 0 0 c o s α i − 1 − s i n α i − 1 0 0 s i n α i − 1 c o s α i − 1 0 0 0 0 1 ] R o t_{x}\left(\alpha_{i-1}\right)=\begin{bmatrix}1 &0&0&0\\ 0&cos\alpha_{i-1}&{-sin\alpha_{i-1}}&0\\0&{sin\alpha_{i-1}}&{cos\alpha_{i-1}}&{0}\\ {0}&{0}&{0}&{1}\end{bmatrix} Rotx(αi−1)=⎣⎢⎢⎡10000cosαi−1sinαi−100−sinαi−1cosαi−100001⎦⎥⎥⎤ - 沿
x
i
−
1
x_{i-1}
xi−1轴移动
a
i
−
1
a_{i-1}
ai−1
T r a n s x ( a i − 1 ) = [ 1 0 0 a i − 1 0 1 0 0 0 0 1 0 0 0 0 1 ] T r a n s_{x}\left(a_{i-1}\right)=\begin{bmatrix}1 &0&0&a_{i-1}\\ 0&1&0&0\\0&0&1&{0}\\ {0}&{0}&{0}&{1}\end{bmatrix} Transx(ai−1)=⎣⎢⎢⎡100001000010ai−1001⎦⎥⎥⎤ - 沿
z
i
z_{i}
zi轴移动
θ
i
\theta_{i}
θi
R o t z ( θ i ) = [ c o s θ i − s i n θ i 0 0 s i n θ i c o s θ i 0 0 0 0 1 0 0 0 0 1 ] R o t_{z}\left(\theta_{i}\right)=\begin{bmatrix}{cos\theta_{i}}&{-sin\theta_{i}}&0&0\\ {sin\theta_{i}}&{cos\theta_{i}}&0&0\\0&0&1&0\\ {0}&{0}&{0}&{1}\end{bmatrix} Rotz(θi)=⎣⎢⎢⎡cosθisinθi00−sinθicosθi0000100001⎦⎥⎥⎤ - 沿
z
i
z_{i}
zi轴移动
d
i
d_{i}
di
T r a n s z ( d i ) = [ 1 0 0 0 0 1 0 0 0 0 1 d i 0 0 0 1 ] T r a n s_{z}\left(d_{i}\right)=\begin{bmatrix}1 &0&0&0\\ 0&1&0&0\\0&0&1&d_i\\ {0}&{0}&{0}&{1}\end{bmatrix} Transz(di)=⎣⎢⎢⎡10000100001000di1⎦⎥⎥⎤
这些变换都是相对运动坐标系描述的，满足从左到右的原则，可以得到最终变换公式如下：
i
i
−
1
T
=
R
o
t
x
(
α
i
)
T
r
a
n
s
x
(
a
i
)
R
o
t
z
(
θ
i
)
T
r
a
n
s
z
(
d
i
)
_{i}^{i-1}T=R o t_{x}\left(\alpha_{i}\right)T r a n s_{x}\left(a_{i}\right)R o t_{z}\left(\theta_{i}\right)T r a n s_{z}\left(d_{i}\right)
ii−1T=Rotx(αi)Transx(ai)Rotz(θi)Transz(di)
通常规定
a
i
≥
0
a_i\ge0
ai≥0，因为它代表连杆长度，而
α
i
,
d
i
,
θ
i
\alpha_i, d_i, \theta_i
αi,di,θi可正可负。
i i − 1 T = [ c o s θ i − s i n θ i 0 a i − 1 s i n θ i c o s α i − 1 c o s θ i c o s α i − 1 − s i n α i − 1 − d i s i n α i − 1 s i n θ i s i n α i − 1 c o s θ i s i n α i − 1 c o s α i − 1 d i c o s α i − 1 0 0 0 1 ] _{i}^{i-1}T=\begin{bmatrix}{cos\theta_{i}}&{-sin\theta_{i}}&0&{a _{i-1}}\\ {sin\theta_{i}cos\alpha_{i-1}}&{cos\theta_{i}cos\alpha_{i-1}}&{-sin\alpha_{i-1}}&{-d_isin\alpha_{i-1}}\\{sin\theta_{i}sin\alpha_{i-1}}&{cos\theta_{i}sin\alpha_{i-1}}&{cos\alpha_{i-1}}&{d_icos\alpha_{i-1}}\\ {0}&{0}&{0}&{1}\end{bmatrix} ii−1T=⎣⎢⎢⎡cosθisinθicosαi−1sinθisinαi−10−sinθicosθicosαi−1cosθisinαi−100−sinαi−1cosαi−10ai−1−disinαi−1dicosαi−11⎦⎥⎥⎤
2.Matlab符号运算验证
利用Matlab的符号运算进行公式推导进行一下公式的验证文章来源：https://www.toymoban.com/news/detail-430463.html
syms theta d alpha a
M=DH_Trans(theta,d,alpha,a)
function M=DH_Trans(theta,d,alpha,a)
R_z_theta=[cos(theta),-sin(theta),0,0;...
sin(theta),cos(theta),0,0;...
0,0,1,0;...
0,0,0,1];
T_z_d=[1,0,0,0;...
0,1,0,0;...
0,0,1,d;...
0,0,0,1];
R_x_alpha=[1,0,0,0;...
0,cos(alpha),-sin(alpha),0;...
0,sin(alpha),cos(alpha),0;...
0,0,0,1];
T_x_a=[1,0,0,a;...
0,1,0,0;...
0,0,1,0;...
0,0,0,1];
M=R_x_alpha*T_x_a*R_z_theta*T_z_d;
end
结果是一致的
文章来源地址https://www.toymoban.com/news/detail-430463.html
到了这里，关于机器人学DH参数及利用matlab符号运算推导的文章就介绍完了。如果您还想了解更多内容，请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章，希望大家以后多多支持TOY模板网！
