1. 前言
对于基环树的讲解,分上、下 2 篇,上篇以理解连通分量、环以及使用深度搜索算法检查连通性和环为主,下篇以基于基环树结构的应用为主。
什么是基环树?
所谓基环树指由n个节点n条边所构建而成的连通图。
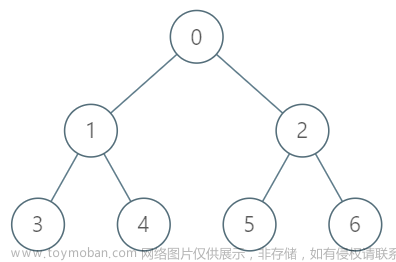
如下图所示,树结构中共有 7 个节点, 6 条边。此时在树结构上添加一条边,必然会形成一个树环。因树结构中有环,故得此名。基环树也称为环套树。

如下图基环树结构中有 7 个节点,7 条边。

上述为无向边基环树。针对于有向边,基环树分:
-
内向树:树中每个点有且仅有一条出边(或者说每个节点的出度为
1)。

-
外向树:树中每个点有且仅有一条入边(或者说每个点的入度为
1)。

基于基环树有一项基本操作,寻找基环树上的环。
下文将深入讲解如何使用深度搜索算法在无向图中查找环结构。
2. 查找环
在图中查找环的常用的算法有:
- 深度搜索算法。
- 广度搜索算法。
- 并查集。
- 拓扑排序算法。
广度和深度搜索是原生算法,面对较复杂的图结构时,略显拙劣。较优的方案是使用优化过的并查集和拓扑排序算法,其在性能和技巧上都很精妙。
Tips: 关于并查集和拓扑排序算法可查阅我的相关博文。
2.1 问题分析
起点和终点相同的路径称为回路或称为环(Cycle),除第一个顶点与最后一个顶点之外,其他顶点不重复出现的回路称为简单回路,本文仅对简单回路进行讨论。
Tips: 一般而言,回路至少需要
3个顶点。
图中是否有环的前提条件:边数至少要等于顶点数。
所以对于有 n个顶点的无向(有向)图,是否存在环,可以先检查边的数量 m与顶点数量之间的关系。
Tips: 本文主要以无向图为讨论对象。
- 如果
m=n-1。可以是下面的几种情况。
-
一个连通分量图情况。可以理解为以任何一个顶点为根节点构建成的树结构,此时连通分量为
1,显然此情况无法成环。Tips: 所谓连通图,指任意两个顶点之间都有路径的图。


-
上文说过,如果存在回路,顶点数量和边数至少要相等,这句话不能狭义地诠释为如果边数小于顶点数,则图中无环。
当
m=n-1时,顶点数可以拆分成n=m+1。这里遵循一个拆分原则,尽可能在已有边数的基础上成全图中某些顶点成环的要求。如下图所示,连通分量有
2个,其中一个子图中存在一个环。所以当边数少于顶点数时,需要讨论是否存在子图。

也可以是如下几种图形:


-
m<n-1时,如果m<=2则无法构建成环。其它情况下都能构建出一个有环的子图。

- 当
m>=n因为边数已经大于顶点数,显然图中有环。



2.2 深度搜索算法思想
2.2.1 连通分量
可以使用深度搜索算法查找图中是否有环,先了解一下深度搜索算法的搜索流程。
Tips: 深度搜索算法可以使用递归和非递归实现。本质是使用栈进行数据存储。
- 先创建一个栈(非递归实现),用来存储搜索到的顶点。

- 以
A顶点为出发点,且把A顶点压入栈中,用于初始化栈。并在图的A顶点上做已入栈的标志。

- 查询出与
A顶点相邻的顶点B、E,并且压入栈中。

- 继续查询与
E顶点相邻的顶点(即入栈操作完成后,再查询与栈顶元素相邻的顶点)D,且压入栈中。

- 检查与
D顶点相邻的顶点C,且压入栈中。

经过上述操作后,可发现图结构中所有顶点全部被压入栈中,此时,能证明什么?
至少有一点是可以证明的:栈中的顶点在一个集合或在一个连通分量上。
使用如上搜索方案时,是否能找到此连通分量上的所有顶点?
先看下图的搜索结果:
当查询与 D顶点相邻的顶点时,因 D和C没有连通性,故C无法入栈。栈中的顶点在一个连通分量上,是不容质疑的,而实际上 C也是此连通分量上的一份子。

所以,使用仅入栈不出栈的搜索方案,无法找到同一个连通分量上的所有顶点。
可以把深度搜索方案改一下,采用入栈、出栈形式。
- 初始
A入栈。

-
A出栈,找到与A相邻的顶点B、E,且入栈。

-
E出栈,找到与E相邻的D顶点,且让其入栈。

-
D出栈,因没有与D相邻的顶点(每个顶点只能入一次栈)可入栈。继续B出栈,因C是与之相邻的顶点且没有入过栈,C入栈。

- 最后
C出栈,栈空。

至此,可以得到一个结论:
- 在一次深度搜索过程中,入过栈的顶点都在一个集合中(或一个连通分量上)。
- 使用出栈、入栈方案时,可以保证搜索到一个连通分量上的所有顶点。
**Tips: **使用广度搜索一样能找到一个连通分量上的所有顶点。
原理很简单,深度搜索是按纵深方式进行搜索的(类似于一条线上的蚂蚱),在互相有关联的纵深线上的顶点能被搜索到。
如下图所示:从A开始,有左、右两条纵深线,在搜索完左边的纵深线后。

可以继续搜索另一条纵深线。

一次深度搜索只能检查到一条连通分量。如果图中存在多个连通分量时,需要使用多次深度搜索算法。如下图所示:

连通分量与找环有什么关系?
连通分量与环之间有很一个简单的关系:环一定是存在一个连通分量上。找环之前,先要确定目标顶点是不是在一个连通分量上。否则,都不在一起,还找什么环?
是否在一个连通分量上的顶点一定有环?
如下图,所有顶点都在一个连通分量中,实际情况是,图没有环。所以,仅凭顶点全部在一个连通分量上,是无法得到图中一定有环的结论。

那么,使用深度搜索算法在图中搜索时,怎么证明图中有环?
根据前面的推断,可以得出结论:
- 所有搜索的顶点在一个连通分量上,且图或子图边数大于或等于顶点数时,那么图或子图中必然存在环。

那么?环上的顶点有什么特点?
如果图中存在环,那么,环上每个顶点必然至少有 2条边分别和环上另 2 个顶点相连,边的数量决定与其相邻顶点的数量。
Tips:道理很简单,如果有
n个人通过手牵手围成一个圈,如果其中有一个人只原意出一只手,则圈是无法形成的。 可以把此人移走,剩余人可以围成一个圈。

2.2.2 小结
查询环上的顶点时,需要满足如下几个要求:
- 所有顶点在一个连通分量上。
- 连通分量上的边数要大于或等于顶点数。
- 环上至少有
2条边的顶点可认定是环上的顶点。
2.3 编码实现
顶点类:
#include <iostream>
#include <vector>
#define MAXVERTEX 10
using namespace std;
/*
*顶点类
*/
struct Vertex {
//编号
int vid;
//数据
char val;
//与之相邻的边数
int edges;
//是否访问过
bool isVisited;
//前驱节点编号
int pvid;
Vertex() {
this->vid=-1;
this->edges=0;
this->isVisited=false;
}
Vertex(int vid,char val) {
this->vid=vid;
this->edges=0;
this->val=val;
this->isVisited=false;
}
};
图类: 先在图类提供常规API(对顶点的维护函数,添加顶点和添加顶点之间的关系)。
/*
* 图类
*/
class Graph {
private:
//所有顶点
Vertex allVertex[MAXVERTEX];
//二维矩阵,存储顶点关系(边)
int matrix[MAXVERTEX][MAXVERTEX];
//顶点数量
int num;
public:
Graph() {
this->num=0;
for(int i=0; i<MAXVERTEX; i++) {
for(int j=0; j<MAXVERTEX; j++) {
this->matrix[i][j]=0;
}
}
}
/*
*添加顶点,返回顶点编号
*/
int addVertex(char val) {
Vertex ver(this->num,val);
this->allVertex[this->num]=ver;
return this->num++;
}
/*
*添加顶点之间的关系
*/
void addEdge(int from,int to) {
//无向图中,需要双向添加
this->allVertex[from].edges++;
this->matrix[from][to]=1;
this->allVertex[to].edges++;
this->matrix[to][from]=1;
}
/*
*深度搜索算法找环
*/
void findCycle() { }
/*
*显示矩阵中边信息
*/
void showEdges() {
for(int i=0; i<this->num; i++) {
for(int j=0; j<this->num; j++) {
cout<<this->matrix[i][j]<<"\t";
}
cout<<endl;
}
}
};
下图的子图A、B、E、D就是基环树。现使用代码构建下图:

//测试
int main() {
Graph graph;//=new Graph();
//添加顶点
int aid= graph.addVertex('A');
int bid= graph.addVertex('B');
int cid= graph.addVertex('C');
int did= graph.addVertex('D');
int eid= graph.addVertex('E');
//添加顶点之间关系
graph.addEdge(aid,bid); //A ---- B
graph.addEdge(aid,eid); //A --- E
graph.addEdge(bid,eid); //B ---- E
graph.addEdge(did,eid); // E----D
graph.showEdges();
return 0;
}
确认图的构建是否正确。

核心函数: 使用深度搜索算法检查图中是否存在环。
/*
*深度搜索算法找环
*/
void findCycle(int from) {
//记录连通分量中的边数
int sides=0;
//栈
stack<int> myStack;
//初始化栈
myStack.push(from);
//标志已经入过栈
this->allVertex[from].isVisited=true;
//存储搜索过的顶点
vector<int> vers;
//出栈操作
while( !myStack.empty() ) {
//出栈
int vid= myStack.top();
//存储搜索顶点
vers.push_back(vid);
//删除
myStack.pop();
//检查相邻节点
for(int i=0; i<this->num; i++ ) {
if( this->matrix[vid][i]==1 ) {
// i 是 from 的相邻顶点
sides++;
//标志此边已经被记录
this->matrix[vid][i]=-1;
if(this->allVertex[i].isVisited==false ) {
//边对应顶点是否入过栈
myStack.push(i);
this->allVertex[i].isVisited=true;
}
}
}
}
//输出搜索结果
cout<<"输出连通分量中的顶点:"<<endl;
for(int i=0; i<vers.size(); i++)
cout<< this->allVertex[vers[i]].val<<"\t";
cout<<endl;
//存储搜索结果
allConns.push_back(vers);
//检查环
if(sides>=vers.size() && vers.size()>3 ) {
//边数大于或等于搜索过的顶点数。表示搜索过的顶点在一个集合中,且有环
cout<<"存在环:"<<endl;
for(int i=0; i<vers.size(); i++) {
if( this->allVertex[vers[i]].edges>=2 ) {
cout<<this->allVertex[vers[i]].val<<"->\t";
}
}
cout<<endl;
}
//检查是否还有其它连通分量
for(int i=0; i<this->num; i++) {
bool isExist=false;
//是否已经搜索
for(int j=0; j<allConns.size(); j++) {
auto res = find( begin( allConns[j] ), end( allConns[j] ),this->allVertex[i].vid );
if(res!=end(allConns[j] ) ) {
//搜索过
isExist=true;
break;
}
}
if(!isExist) {
findCycle(this->allVertex[i].vid );
}
}
}
//显示图中所有连通分量
void showConn() {
cout<<"图中存在"<<allConns.size()<<"个连通分量"<<endl;
}
测试:
int main() {
//省略……
graph.showEdges();
graph.findCycle(0);
graph.showConn();
graph.showEdges();
return 0;
}
输出结果:

3. 总结
本文讲解怎么使用深度搜索算法在无向图中查找环,当然,也可以使用广度搜索算法实现。文章来源:https://www.toymoban.com/news/detail-430804.html
检查图中连通性的最好的方案是使用并查集。文章来源地址https://www.toymoban.com/news/detail-430804.html
到了这里,关于C++ 树进阶系列之探讨深度搜索算法查找环的细枝末节的文章就介绍完了。如果您还想了解更多内容,请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章,希望大家以后多多支持TOY模板网!