相关文章
数字IC前端专栏https://blog.csdn.net/weixin_45791458/category_12173698.html?spm=1001.2014.3001.5482
-
引言
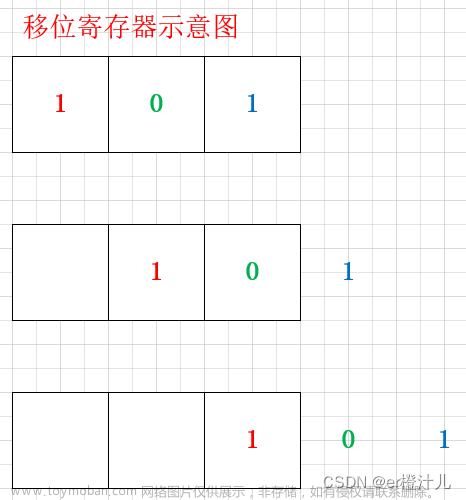
LFSR(线性反馈移位寄存器)用于产生可重复的伪随机序列PRBS(Pseudo-Random Binary Sequence),结构包括n级D触发器和一些异或门(或同或门)组成,在每个时钟沿,后级D触发器输出会以某种方式反馈至前级电路,而反馈结果为某些寄存器的输出进行异或运算得到。
LFSR的初始值被称为序列的种子,末级触发器在循环输出同一个伪随机序列(特别的,对于斐波那契LFSR,每一个触发器都在循环输出同一个伪随机序列)。由n个触发器构成的LFSR电路可以产生的伪随机序列长度为2^n-1(减一是因为对于异或门构成的LFSR,全0状态是不允许存在的,因为0无论怎么异或,结果都是0,这会进入死循环,对于同或门构成的LFSR,全1状态不允许存在,理由同上)。目前有两类常用的LFSR:斐波那契LFSR和伽罗瓦LFSR,下面分别介绍。
-
斐波那契LFSR和伽罗瓦LFSR
(1)斐波那契LFSR(又称外反馈LFSR、多到一LFSR),即多个触发器的输出通过异或逻辑驱动最前级的一个触发器,具体电路如下图所示。

在该例中,x3和x2输出的结果异或运算并连接到最前级x1的输入,反馈多项式意思即为在x3和x2的输出处有抽头反馈。而且可以看到异或门的反馈是在外部的(即异或门的输入和输出连接的并不是相邻寄存器)。
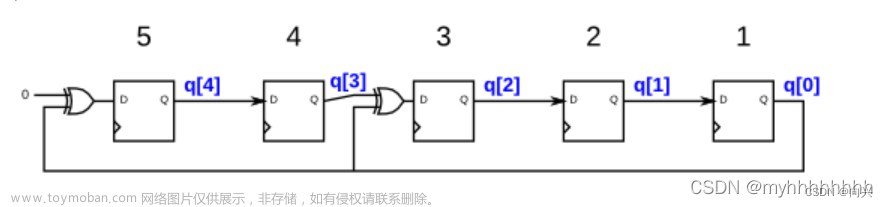
(2)伽罗瓦LFSR(又称内反馈LFSR、一到多LFSR),即最后级触发器的的输出和前级各级触发器的输出异或运算驱动下一级触发器,具体电路如下图所示。

在该例中,最后一级触发器的输出和x3输出的结果异或运算并连接到x3的下一级x2的输入,而且可以看到异或门的反馈是在内部的(即异或门的一个输入和输出连接的是相邻寄存器)。
-
LFSR的用法
LFSR具有广泛的应用,下面对其中的一些典型应用进行介绍。
LFSR计数器
LFSR可用于构造通过随机状态进行计数的计数器。与常见的计数器相比,LFSR计数器具有速度快、消耗逻辑门少的特点。
扰码器/解扰器
LFSR可用作扰码器来产生重复的比特图案。当重复间隔较大时,该比特图案看上去就像一个随机的比特序列。用户数据发送前和扰码器生成的序列进行异或,然后发出,此时发送的数据就是经过扰码的数据。接收电路采用与发送电路相同的多项式,这样,解扰器就可以将发送端原始的用户数据恢复出来。(注:与同一个数连续异或两次,最终结果是自身)文章来源:https://www.toymoban.com/news/detail-431117.html
以上内容来源于《Verilog高级数字系统设计技术和实例分析》文章来源地址https://www.toymoban.com/news/detail-431117.html
到了这里,关于数字IC前端学习笔记:LSFR(线性反馈移位寄存器)的文章就介绍完了。如果您还想了解更多内容,请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章,希望大家以后多多支持TOY模板网!