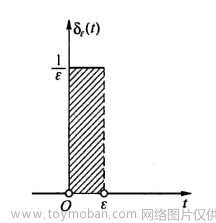
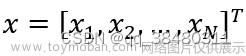深入理解傅里叶变换（一）-Toy模板网

这篇具有很好参考价值的文章主要介绍了深入理解傅里叶变换（一）。希望对大家有所帮助。如果存在错误或未考虑完全的地方，请大家不吝赐教，您也可以点击"举报违法"按钮提交疑问。

三棱镜分解太阳光实验

深入理解傅里叶变换（一）
三棱镜能将太阳光分解成七种颜色的可见光。我们知道这七种颜色有不同的波长范围，从而对应不同的频率范围。这给我们一个启示：太阳光这种看起来是白色的光，其实是由不同频率的光组成的，而三棱镜能起到将太阳光分解成不同频率的光的作用。

如果把三棱镜看作是一个算法，把太阳光看作是一段信号，那么我们就可以设想：存在一种算法，能将一段信号分解成不同频率的信号。

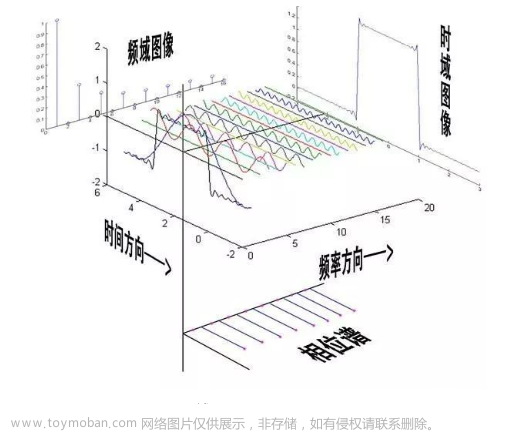
从时域到频域

深入理解傅里叶变换（一）
上图表示的是同一段信号，左图为时域图，右图为频域图，频域图中y轴的值最大的那个尖峰（即第二个尖峰）是时域信号最为重要的一个分量（或者说，最为相似的一个分量），而第一个尖峰所对应的频率则被称为基频F0。

那么该如何做这个分解呢，直观来看，分为以下几个步骤：

将原始时域信号，与不同频率的正弦信号，比较相似度
比较相似度的结果是，我们得到不同频率的正弦信号对应的振幅和初相
正弦信号的振幅越大，该频率的正弦信号与原始时域信号的相似度就越大

傅里叶变换

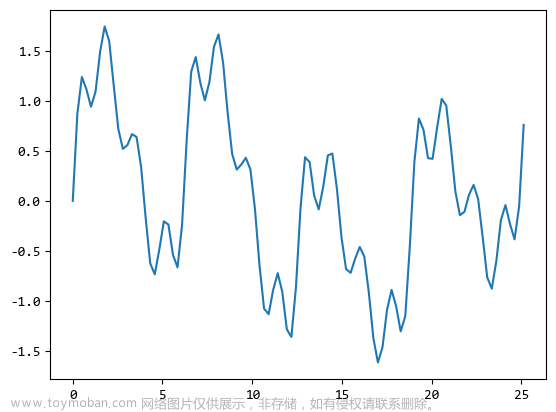
加载一段音频信号，指定采样率为16000Hz，然后绘制出其时域图像

import librosa
import librosa.display
import matplotlib.pyplot as plt
import numpy as np
import scipy as sp


def wav_to_ft(filename):
    signal, sr = librosa.load(filename, sr=16000)
    librosa.display.waveshow(y=signal, sr=sr, alpha=0.5)

    plt.show()


if "__main__" == __name__:
    filename = r"10 - Fourier Transform_ The Intuition\audio\piano_c.wav"
    wav_to_ft(filename)

深入理解傅里叶变换（一）
然后使用FFT，得到不同频率对应的振幅和初相，注意：

不同的频率是通过将采样频率等分得到的
这里的是振幅和初相是用复数给出的，需要求模长得到振幅
初相一般在机器学习中不重要，所以略去

def wav_to_ft(filename):
    signal, sr = librosa.load(filename, sr=16000)
    ft = np.fft.fft(signal)
    magnitude = np.abs(ft)
    frequency = np.linspace(0, sr, len(magnitude))

    plt.subplot(1, 2, 1)
    librosa.display.waveshow(y=signal, sr=sr, alpha=0.5)

    plt.subplot(1, 2, 2)
    plt.plot(frequency, magnitude)
    plt.xlabel("Frequency Hz")
    plt.ylabel("Magnitude")

    plt.show()

深入理解傅里叶变换（一）
惊奇的发现FFT得到的频率-振幅图像是对称的，原因暂且按下不表。由于对称性，我们可以只显示一半的图像，即(1+sr//2)。

plt.plot(frequency[:1 + sr // 2], magnitude[:1 + sr // 2])

深入理解傅里叶变换（一）
第一个尖峰对应频率：524Hz
第二个尖峰对应频率：1053Hz
第三个尖峰对应频率：1591Hz
第四个尖峰对应频率：2136Hz
近似为等差数列，理论上而言，的确应该为等差数列。即第一个尖峰为基波（基音），其他的为基频整数倍的尖峰为谐波（泛音）。

如何寻找这些正弦波

基波频率为524Hz，则一个基波周期为1/524Hz=0.0019s，大概为2ms，而一个采样的持续时间为1/16000Hz=0.0000625s，即32个采样点的持续时间大概为一个基波周期。

我们就取出原始信号的一个320个采样点的局部，大概为十个基波周期，看看这个局部范围内的信号是如何找寻基波的初相的。

def wav_to_ft(filename):
    signal, sr = librosa.load(filename, sr=16000)
    ft = np.fft.fft(signal)
    magnitude = np.abs(ft)
    phase = np.angle(ft)
    frequency = np.linspace(0, sr, len(magnitude))

    samples = range(len(signal))
    time = librosa.samples_to_time(samples=samples, sr=sr)

    f0, voiced_flag, voiced_probs = librosa.pyin(y=signal,
                                                 fmin=librosa.note_to_hz('C2'),
                                                 fmax=librosa.note_to_hz('C7'),
                                                 sr=sr)
    fs = [int(f0[1]), 2 * int(f0[1]), 3 * int(f0[1])]

    mag0 = 0.5
    phase0 = phase[fs[0]]
    sin0 = mag0 * np.sin(2 * np.pi * fs[0] * time + phase0)

    mag1 = 0.5
    phase1 = phase0 + 2 * np.pi * 0.3
    sin1 = mag1 * np.sin(2 * np.pi * fs[0] * time + phase1)

    mag2 = 0.5
    phase2 = phase0 + 2 * np.pi * 0.5
    sin2 = mag2 * np.sin(2 * np.pi * fs[0] * time + phase2)

    mul0 = sin0 * signal
    mul1 = sin1 * signal
    mul2 = sin2 * signal

    # plt.subplot(1, 2, 1)
    # librosa.display.waveshow(y=signal, sr=sr, alpha=0.5)

    # plt.subplot(1, 2, 2)
    # plt.plot(frequency[:1 + sr // 2], magnitude[:1 + sr // 2])
    # plt.xlabel("Frequency Hz")
    # plt.ylabel("Magnitude")

    fig, ax = plt.subplots(3, 1, sharex=True)
    ax[0].plot(time[1000:1000 + 320], signal[1000:1000 + 320])
    ax[0].plot(time[1000:1000 + 320], sin0[1000:1000 + 320])
    ax[0].fill_between(time[1000:1000 + 320], mul0[1000:1000 + 320])

    ax[1].plot(time[1000:1000 + 320], signal[1000:1000 + 320])
    ax[1].plot(time[1000:1000 + 320], sin1[1000:1000 + 320])
    ax[1].fill_between(time[1000:1000 + 320], mul1[1000:1000 + 320])

    ax[2].plot(time[1000:1000 + 320], signal[1000:1000 + 320])
    ax[2].plot(time[1000:1000 + 320], sin2[1000:1000 + 320])
    ax[2].fill_between(time[1000:1000 + 320], mul2[1000:1000 + 320])

    plt.show()

深入理解傅里叶变换（一）
频率已限制为基频，振幅设置为最接近原始信号的0.5，接下来就是寻找使得该正弦波与原始信号相似度最大的初相，一个直观的办法是将对应采样点的信号全部对应相乘，然后累加起来，使得该累加值最大的初相就是要找的初相。

上图中的蓝色填充就是两信号相乘后的值，可见，当最准确的初相变化半个周期后，值全部变为负。

因此，寻找一个正弦波分量的直观过程如下：

选择一个频率
在该频率下，设定振幅为1，然后寻找使两信号相乘再相加后，取得最大值的初相
计算对应的振幅
对于振幅，之前已经提到过，振幅表征了该正弦波与原始信号的相似度，所以振幅就是两信号相乘再相加后的累加值。

对于傅里叶变换，需要在所有可能的频率取值中，迭代地进行上述找寻正弦波分量的过程。

寻找一个正弦波分量的公式表述如下：
$\begin{aligned} \varphi_f &= argmax_{\varphi \in [0,1)} (\int s(t) \cdot sin[2 \pi (ft - \varphi )] \cdot dt ) \\ d_f &= (\int s(t) \cdot sin[2 \pi (ft - \varphi_f )] \cdot dt ) \end{aligned}$
下一部分将与傅里叶变换的数学有关文章来源地址https://www.toymoban.com/news/detail-431131.html