IRB 1600-6/1.45 ABB 改进DH参数计算正解逆解-Toy模板网

这篇具有很好参考价值的文章主要介绍了IRB 1600-6/1.45 ABB 改进DH参数计算正解逆解。希望对大家有所帮助。如果存在错误或未考虑完全的地方，请大家不吝赐教，您也可以点击"举报违法"按钮提交疑问。

一、参考文章

最近在项目中，需要通过笛卡尔空间已知点的位置求解机器人关节空间的状态，最终选择最优方式到达目标点。实验室正好有ABB机器人，型号为IRB 1600-6/1.45。
方法步骤：
1、获取机器人DH参数
2、fk、ik代码
3、robotstudio验证

abb dh参数获取：
dh参数1
dh参数2

参考视频：哔哩哔哩，强烈推荐
台大机器人运动学

fk-ik计算推导参考：
fk-ik2
fk_ik2

二、改进DH参数获取

在上文链接中，按照链接1、2所述，获取到的DH参数应为MDH，其获取结果如下图所示，但是通过最终验证，只有欧拉角计算正确，空间位置并不正确。
IRB 1600-6/1.45 ABB 改进DH参数计算正解逆解

后续通过其他途径获取相关改进DH参数，见下述内容，如有需要，见私信。

三、fk推导

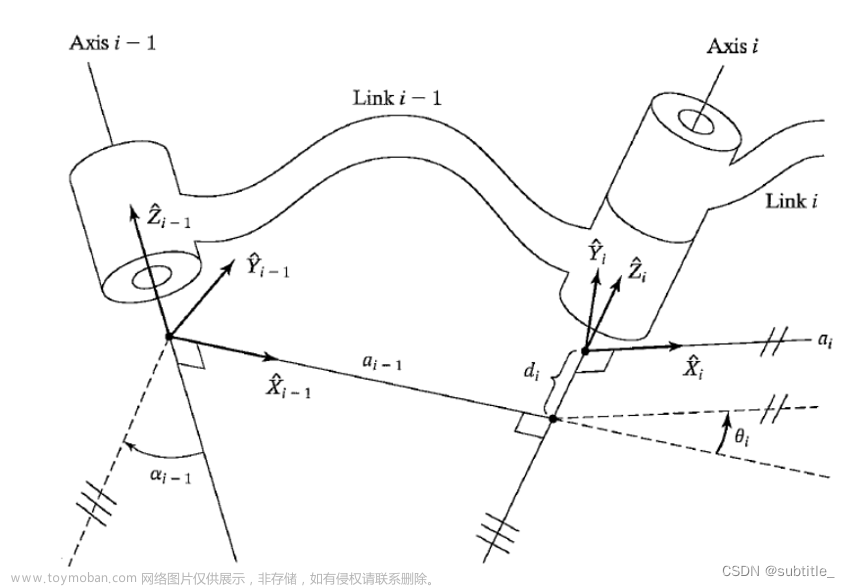
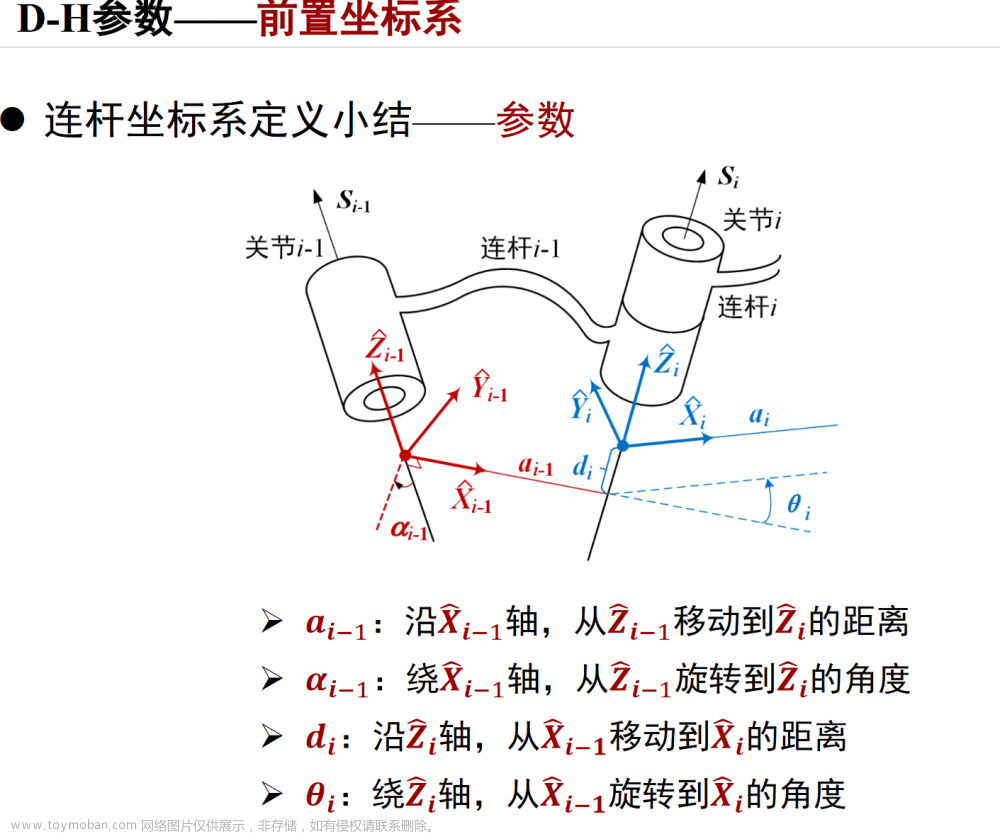
根据上述链接，建立相关坐标系，建立过程如下图所示；
IRB 1600-6/1.45 ABB 改进DH参数计算正解逆解

以课程中示例所示，第i-1与第i杆之间坐标经历α(i-1)，a(i-1)，θ(i）,d(i)。该方法为改进DH参数。其中：
α(i-1) 表示第i-1坐标系z轴经旋转后与第i坐标系z轴平行,逆时针为正；
a(i-1) 表示经过上述操作后的第i-1坐标系z轴与第i坐标系z轴异面直线距离；
θ(i）表示经过上述操作后的第i-1坐标系x轴经旋转后与第i坐标系x轴平行；
d(i) 表示经过上述操作后的i-1坐标系与第i坐标系之间偏移距离。

注意初始坐标系与末尾坐标系中参数，具体见推荐课程。
参考fk-ik2链接中图片，对ABB六轴机器人建立对应的坐标系，轻易可得：

IRB 1600-6/1.45 ABB 改进DH参数计算正解逆解
可得ABB中对应的MDH为，具体型号见技术参数：

最终变换公式如下图所示，T的左上角为以哪一个坐标系作为基准。将上表中数带入下图公式，最终可以得到机器人正解。

最终，将变换矩阵转换为XYZABC格式，只需将旋转矩阵转换为欧拉角即可。

四、ik推导

针对ik推导，具体推导公式不详细列出，最终结果存在多解，为下图所示；
IRB 1600-6/1.45 ABB 改进DH参数计算正解逆解

懒得写了，抽时间再写，依据上述链接中计算后续的theta。

五、测试验证

打开robotstudio，建立机器人工程，打开虚拟示教器，随意设定一个位姿，分别记录笛卡尔空间坐标与关节空间状态，如下图所示，分别进行fk ik计算。
IRB 1600-6/1.45 ABB 改进DH参数计算正解逆解
最终得到位姿如下图所示：
可以看出fk、ik计算正确，为了验证其他关节状态是否正确，分别移动虚拟示教器，让关节状态满足其余七个状态，记录笛卡尔坐标。

关节空间验证

大概位姿，非准确，只是测试是否准确：
第2组、
IRB 1600-6/1.45 ABB 改进DH参数计算正解逆解

第3组、第4组中第五轴超出量程范围；
第5组：

第6组
IRB 1600-6/1.45 ABB 改进DH参数计算正解逆解

第7组、第8组中二轴的超出量程范围；

综上，可以验证abb机器人正解及逆解的正确性；文章来源地址https://www.toymoban.com/news/detail-431335.html

附录-代码部分

#include <iostream>
#include <cmath>
#include <vector>
#include <Eigen/core>
#include <cmath>
using namespace std;
const double pi = 3.14159265397932384626433;

//MDH参数
vector<double> joints_alpha = { 0, -90, 0, 90, -90, 90 };
vector<double> joints_a = { 0, a1, -a2, -0, 0, 0 };
vector<double> joints_d = { d1, 0, 0, d4, 0, d6 };
vector<double> joints_theta = { 0, 90, 0, 0, 0, 0 };
//MDH参数-矩阵
Eigen::Matrix4d dh_matrix(double alpha, double a, double d, double theta);

//旋转矩阵转换为欧拉角
vector<double> computeEularAngles(Eigen::Matrix4d & R, bool israd);

//欧拉角转换为旋转矩阵 xyzabc
Eigen::Matrix4d computeTrans(vector<double> pos);

//fk计算
vector<double> fk_robot(vector<double>joints_alpha, vector<double> joints_a, vector<double> joints_d, vector<double> joints_theta);

//ik计算
vector<vector<double>> ik_robot(Eigen::Matrix4d trans);

int main()
{

	vector<double> temp_theta = { 20.24,14.44,24.48,-22.07,26.14,-84.27 };//关节空间表示
	vector<double> pos = { 773.17,273.55,730.15,-60.93,-14.71,-155.71 };//笛卡尔空间表示

	 //fk 
	vector<double> theta1;
	for (int i = 0; i < joints_theta.size(); i++)
	{
		theta1.push_back(joints_theta[i]+ temp_theta[i]);
	}
	auto rst = fk_robot(joints_alpha, joints_a, joints_d, theta1);
	
	cout << "笛卡尔空间表示：\n"<<"x: "<<rst[0] << "\ty: " << rst[1] << "\tz:" << rst[2] << "\tA: " << rst[3] << "\tB: " << rst[4] << "\tC: " << rst[5] << endl;


	//ik计算
	auto test = computeTrans(pos);
	auto joint=ik_robot(test);

	cout << "关节空间表示：" << endl;
	for (int i = 0; i < joint.size(); i++)
	{
		for (int j = 0; j < joint[i].size(); j++)  cout << "theta"+ to_string(j)+":   "<<joint[i][j] << "\t";
		cout << "\n";
	}

	system("pause");
	return 0;
}