如果你使用 Python 处理数据,你可能听说过 statsmodel 库。Statsmodels 是一个 Python 模块,它提供各种统计模型和函数来探索、分析和可视化数据。该库广泛用于学术研究、金融和数据科学。在本文中,我们将介绍 statsmodel 库的基础知识、如何使用它以及它的好处。

什么是 Statsmodel 库?
Statsmodels 是一个 Python 模块,它提供各种统计模型和函数来探索、分析和可视化数据。它是一个构建在 NumPy、SciPy 和 Pandas 库之上的开源库。它广泛应用于学术研究、金融和数据科学。
Statsmodels 有很多特性,包括:
- 线性回归模型
- 广义线性模型
- 时间序列分析
- 多元统计
- 非参数方法
- 稳健的统计方法
- 可视化工具
安装 Statsmodel 库
statsmodel 库的安装很简单。
pip install statsmodels
此命令将安装最新版本的 statsmodel 库。
加载数据
在开始使用 statsmodel 库之前,我们需要加载数据,这使用 pandas 加载数据:
import pandas as pd
df = pd.read_csv('data.csv')
在从名为“data.csv”的 CSV 文件中读取数据。可以将文件名替换为其他需要的数据文件名。
使用 Statsmodel 探索和分析数据
我们已经加载了数据,现在可以开始使用 statsmodel 探索和分析它。我们将在本节中涵盖三个主要主题:描述性统计、数据可视化和假设检验。
1、描述性统计
描述性统计有助于我们了解数据的基本特征。我们可以使用 statsmodel 库中的 describe() 函数来获取描述性统计数据:
import statsmodels.api as sm
print(data.describe())
describe() 函数返回数据的综述、平均值、标准差、最小值、最大值和四分位数。
2、数据可视化
数据可视化是数据分析的重要组成部分。我们可以直接使用matplotlab来进行可视化:
import matplotlib.pyplot as plt
import seaborn as sns
sns.scatterplot(data=data, x='X', y='Y')
plt.xlabel('X')
plt.ylabel('Y')
plt.show()
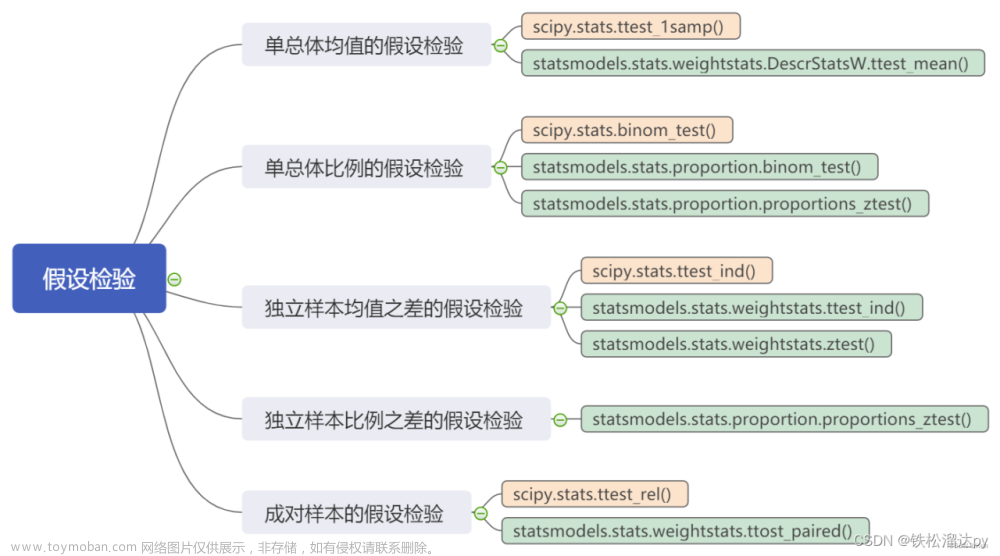
3、假设检验
假设检验是一种检验假设是否成立的统计方法。在 statsmodel 中,我们可以使用 t 检验和 p-value 进行假设检验。
t检验是一种统计方法,用于比较两组数据的均值。它告诉我们两组均值之间的差异是否具有统计显着性。换句话说,它帮助我们确定观察到的两组之间的差异是否可能是偶然的,或者它是否是一个重要的真正差异。t检验是科学研究中常用的一种比较两组数据的比较简单直接的方法。
p-value是统计假设检验中针对原假设的证据强度的度量。它告诉我们在原假设为真的情况下观察到的结果比我们得到的结果更极端的概率。简而言之,它可以帮助我们确定仅靠偶然获得结果的可能性。
如果 p 值非常小(通常小于 0.05),我们可以拒绝零假设并得出观察到的效果具有统计显着性的结论。p值是统计分析中的一个重要概念,在科学研究中被广泛使用。
假设我们要测试线性回归模型中“X”变量的系数是否具有统计显着性。我们可以使用 t 检验和 p 值来检验这个假设:
import statsmodels.formula.api as smf
model = smf.ols('Y ~ X', data=data).fit()
print(model.summary())
summary() 函数将返回一个表格,其中包含线性回归模型的系数、标准误差、t 值和 p 值。
我们可以使用 p 值来检验“X”变量的系数是否具有统计显着性。如果 p 值小于 0.05,我们可以拒绝原假设并得出系数具有统计显着性的结论。
使用 Statsmodel 进行简单线性回归
上面是statsmodel 库的基础知识,让我们更深入地研究线性回归模型。线性回归是一种对因变量与一个或多个自变量之间的关系进行建模的统计方法。我们将介绍使用 statsmodel 的简单线性回归。
上面的代码是对“X”和“Y”变量之间的关系进行建模。我们可以使用 Statsmodel 进行多元线性回归
假设要对“Y”变量与两个自变量“X1”和“X2”之间的关系建模,那么代码如下:
model = smf.ols('Y ~ X1 + X2', data=data).fit()
这里建立了一个线性回归模型,其中“Y”是因变量,“X1”和“X2”是自变量。
总结
本文简单介绍了 statsmodel 库的基础知识以及如何使用它进行统计分析。涵盖了数据操作、汇总统计、假设检验、线性回归模型以及可视化。Statsmodel 是一个强大的库,可以帮助我们轻松地进行复杂的统计分析。广泛应用于金融、经济、社会科学、工程等各个行业。
https://avoid.overfit.cn/post/7e442e350ab340d59d8b8143e4b8c6f1文章来源:https://www.toymoban.com/news/detail-431339.html
作者:panData文章来源地址https://www.toymoban.com/news/detail-431339.html
到了这里,关于使用Statsmodel进行假设检验和线性回归的文章就介绍完了。如果您还想了解更多内容,请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章,希望大家以后多多支持TOY模板网!