对于dfs和bfs,全称为深度优先搜索和广度优先搜索。
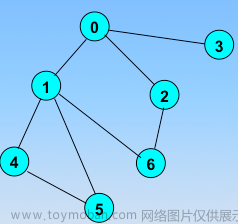
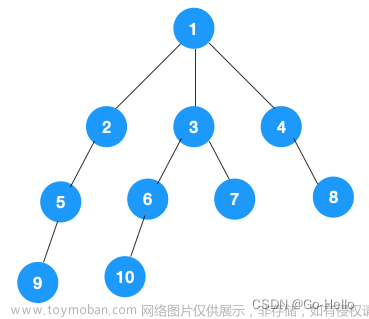
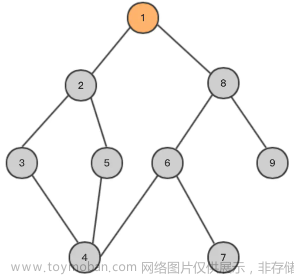
深度优先搜索就是从上一直走到下,如果不能再走,那就回溯,然后再次往下走,直到全部走完或者走到需要的结果返回。例如上图,从0到1,1到3,3到7,不能再走,然后回溯到3,3到8,不能再走;然后回溯到1,1到4,4到9等等等。
广度优先搜索就是一层一层走,直到走到最后一层或者走到需要的结果返回。例如上图,第一层时,然后走到第二层,1和2,然后第三层3、4、5、6,然后一直往下走,因此可以看出广度优先搜索是拥有最短路的性质的,可以相对求出一些最短路问题。
一、dfs
1.全排列问题:最经典的dfs
全排列问题应该是学搜索最开始接触的问题了,以n=3为例,给大家画个图吧。
如图所示,先从1开始,然后2,然后3,发现到了最后;开始回溯,回溯到1再次开始,然后是3,然后是2;开始回溯到2再次开始........大致就是这样一个过程,所有的dfs都是围绕这样一个过程展开的,必须先把底层原理搞清楚,然后再去大量刷题,最后从蒟蒻成为大牛。
给大家写一下代码吧:另外dfs其实就是递归
# include <iostream>
using namespace std;
int n;
int a[30];
bool st[30];
void dfs(int u)
{
if(u>n)
{
for(int i=1;i<=n;i++) cout<<a[i]<<" ";
cout<<endl;
return ;
}
for(int i=1;i<=n;i++)
{
if(st[i]==0)
{
st[i]=1;
a[u]=i;
dfs(u+1);
st[i]=0;
a[u]=0;
}
}
}
int main ()
{
cin>>n;
dfs(1);
return 0;
} 从代码上给大家解释一下吧,输入n以后,进去dfs函数中,也就是递归之中,为啥是递归,因为dfs要回溯,而递归实际上是机器本身会给我们做一个回溯,不用我们自身去进行操作。进入dfs之后,先进行判断,看看是否已经循环到了最底层,如果是,将数全部输入,然后return ,进行回溯处理,另外dfs中需要注意的就是还原现场,因为我们在第一次遍历的过程中,已经将所有数都标记过,如果回溯不还原现场的话,那么将会一直输出此前的结果。
2.经典例题


马走日问题,马走日在算法竞赛中较为常见,给大家写一个如何表示马走日的坐标:
int dx[8] = {-2, -1, 1, 2, 2, 1, -1, -2};
int dy[8] = {1, 2, 2, 1, -1, -2, -2, -1};对于此题来说,一步一步走,那么应该如何来想呢?当给出起点坐标后,我们可以走八个方向,然后其中的一个方向又有八个方向........当我们可以走完所有的格子时,总数加1;如果不能走到的话,那么在限制条件中就会停止,由于递归自己就可以实现回溯,因而并不会出现死循环。
给大家写一下代码,来源于acwing的题:
# include <iostream>
# include <cstring>
using namespace std;
int n,m,sum;
bool st[50][50];
int dx[8] = {-2, -1, 1, 2, 2, 1, -1, -2};
int dy[8] = {1, 2, 2, 1, -1, -2, -2, -1};
void dfs(int x,int y,int cnt)
{
if(cnt==n*m)
{
sum++;
return ;
}
for(int i=0;i<8;i++)
{
int x1=x+dx[i];
int y1=y+dy[i];
if(x1>=0&&x1<n&&y1>=0&&y1<m&&st[x1][y1]==0)
{
st[x1][y1]=1;
dfs(x1,y1,cnt+1);
st[x1][y1]=0;
}
}
}
int main ()
{
int T;cin>>T;
while(T--)
{
int x,y;sum=0;
cin>>n>>m>>x>>y;
memset(st, 0, sizeof st);
st[x][y]=1;
dfs(x,y,1);
cout<<sum<<endl;
}
return 0;
}
二、bfs
1.迷宫问题


走迷宫问题应该算是最经典的bfs模型了,走迷宫大致就是从左上角走到右下角,找一条最短路,这就是利用bfs来做的。用bfs来做,首先需要了解pair二元组和队列的基本知识,dfs是没有模板的,重要的是思路,而bfs有一个基本的模板就是利用队列来做,因为是一层一层来搜索,因此将第一层压入队列中,依次进行搜索,然后将第二层压入队列中,一层一层查找,直到最后的结果。
给大家看一下代码,通过代码理解一下,然后再给大家讲解一下代码:
# include <iostream>
# include <cstring>
# include <queue>
using namespace std;
int n,m;
int a[110][110]; //存储迷宫
int b[110][110]; //存储距离
queue <pair<int,int>> q;
int bfs()
{
int dx[4] = {-1, 0, 1, 0};
int dy[4] = {0, 1, 0, -1};
memset(b,-1,sizeof(b));
q.push({1,1}); //存储第一个点
b[1][1]=0;
while(q.size())
{
auto t=q.front();
q.pop();
for(int i=0;i<4;i++)
{
for(int i=0;i<4;i++)
{
int x=t.first+dx[i];
int y=t.second+dy[i];
if(x>=1&&x<=n&&y>=1&&y<=m&&a[x][y]==0&&b[x][y]==-1)
{
b[x][y]=b[t.first][t.second]+1;
q.push({x,y});
}
}
}
}
return b[n][m];
}
int main ()
{
cin>>n>>m;
for(int i=1;i<=n;i++)
for(int j=1;j<=m;j++)
cin>>a[i][j];
cout<<bfs();
return 0;
}bfs中定义的东西较多,首先是初始输入的数组,然后需要一个数组记录开始到所求结果的距离,然后需要定义一个队列将元素压进去,如上码,输入迷宫后,进去bfs中,将初始位置压入队列中,然后进行一层一层遍历,当一个元素遍历之后,一定要在队列中将此元素删除,否则会一直循环下去,这就是大致过程,最后我们输出右下角的距离数组的元素就行。
2. 矩阵距离(上点难度:多源bfs)


多源bfs其实相对也没那么难,只不过是一般的题只压入一个元素,然后进行遍历,而多源bfs是压入多个元素进行遍历,只要理解单个元素的,多源bfs也就不会有难度了。
# include <iostream>
# include <queue>
# include <cstring>
using namespace std;
int n,m;
char a[1010][1010];
int st[1010][1010];
queue <pair <int,int>> s;
int dx[4] = {-1, 0, 1, 0}, dy[4] = {0, 1, 0, -1};
void bfs()
{
while(s.size())
{
auto t=s.front();
s.pop();
for(int i=0;i<4;i++)
{
int x=dx[i]+t.first;
int y=dy[i]+t.second;
if(x>=0&&x<n&&y>=0&&y<m&&st[x][y]==-1)
{
st[x][y]=st[t.first][t.second]+1;
s.push({x,y});
}
}
}
}
int main()
{
memset(st, -1, sizeof st);
cin>>n>>m;
for(int i=0;i<n;i++)
{
for(int j=0;j<m;j++)
{
cin>>a[i][j];
}
}
for(int i=0;i<n;i++)
{
for(int j=0;j<m;j++)
{
if(a[i][j]=='1')
{
s.push({i,j});
st[i][j]=0;
}
}
}
bfs();
for(int i=0;i<n;i++)
{
for(int j=0;j<m;j++)
{
cout<<st[i][j]<<" ";
}
cout<<endl;
}
return 0;
}看了这么多,我觉得已经不需要我解释代码了,同学们自己就可以理解了。我下来说说我的理解,看看同学们和我的想法一样不。先给大家讲一下题意吧,将需要解决的问题抽丝剥茧出来就是,如果当前为0,那么距离自己最近的1的距离是多少。我的想法就是将所有1压入队列中,再利用bfs,一步一步将所有0都变成1,同时需要另一个数组来记录距离,最后输出即可。
三、总结
其实不论是bfs和dfs,都是暴力搜索,一般数据范围不会太大,而且很多情况下bfs和dfs是可以通用的,也就是一道题既可以用bfs,也可以用dfs。
最后,再给大家来一道两者皆可的题目,必须要吐槽一下这道题,当时还没接触过搜索,但是在我们二次招新中出现了,根本看不懂,我是蒟蒻,我啥都不会。
奇怪的电梯:来源于洛谷


直接给大家上代码了:文章来源:https://www.toymoban.com/news/detail-431464.html
//用bfs做的
# include <iostream>
# include <queue>
using namespace std;
int n,a,b;
int sum;
int lou[300];
int d[300];
int pan[300];
queue <int> s;
int bfs()
{
s.push(a);
while(s.size())
{
auto t=s.front();
pan[t]=1;
s.pop();
int x=t+lou[t];
if(x>=1&&x<=n&&pan[x]==0)
{
d[x]=d[t]+1;
pan[x]=1;
s.push(x);
if(x==b) return d[x];
}
int y=t-lou[t];
if(y>=1&&y<=n&&pan[y]==0)
{
d[y]=d[t]+1;
pan[y]=1;
s.push(y);
if(y==b) return d[y];
}
}
return -1;
}
int main ()
{
cin>>n>>a>>b;
for(int i=1;i<=n;i++) cin>>lou[i];
if(a==b) cout<<"0";
else
cout<<bfs();
return 0;
} //用dfs做的
# include <iostream>
using namespace std;
int n,a,b;
int c[3000];
bool d[3000];
int x=0x7ffffff;
void dfs(int louceng,int num)
{
if(louceng==b) x=min(x,num);
if(num>x) return ;
d[louceng]=1;
if(louceng+c[louceng]<=n&&d[louceng+c[louceng]]==0)
dfs(louceng+c[louceng],num+1);
if(louceng-c[louceng]>=1&&d[louceng-c[louceng]]==0)
dfs(louceng-c[louceng],num+1);
d[louceng]=0;
}
int main ()
{
cin>>n>>a>>b;
for(int i=1;i<=n;i++) cin>>c[i];
d[a]=1;
dfs(a,0);
if(x!=0x7ffffff) cout<<x;
else printf("-1");
return 0;
} 完结撒花文章来源地址https://www.toymoban.com/news/detail-431464.html
到了这里,关于算法之搜索(C++)的文章就介绍完了。如果您还想了解更多内容,请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章,希望大家以后多多支持TOY模板网!