题目链接
题目
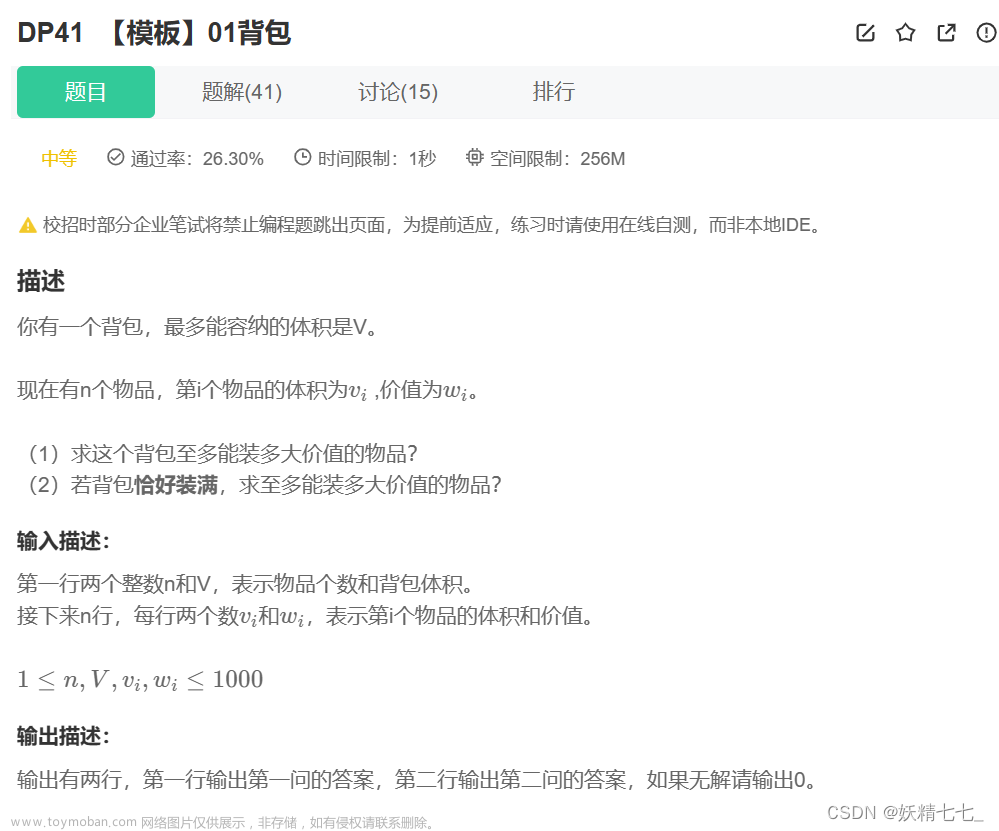
题目描述
I used to believe
We were burning on the edge of something beautiful
Something beautiful
Selling a dream
Smoke and mirrors keep us waiting on a miracle
On a miracle
Say go through the darkest of days
Heaven's a heartbreak away
Never let you go
Never let me down
OH it's been a hell of a ride
Driving the edge of a knife
Never let you go
Never let me down
Bieber拥有一个长度为n的01 串,他每次会选出这个串的一个子串作为曲谱唱歌,考虑该子串从左往右读所组成的二进制数P。 Bieber每一秒歌唱可以让P增加或减少 2 的 k次方(k由Bieber选定),但必须保证任意时刻其P大于等于0。
Bieber 是一位追求效率的人 每次Bieber都想知道他歌唱的最少时间将这个数P变成0。
Bieber 正和 一位DJ合作,他随时可能修改串上的一个字符。
输入描述
第一行一个数n
第二行一个长度为n的字符串s
第三行一个数 t 表示 询问 + 修改总次数
以下 t 行, 每行格式如下
第一个数 1 <= type <= 2 表示 类型
Type = 1 表示是一次 询问 接下来两个数 l , r 表示询问的区间。
否则 表示一次修改 接下来两个数x,y 表示把 s[x] 改为y.
n <= 3e5, t <= 3e5
输出描述
对于每个询问输出一个数表示最少次数。
示例1
输入
4
1101
1
1 1 4
输出
3
题解
知识点:动态dp,区间dp,线段树。
先考虑不带修改操作只有询问,那就是一道简单的区间dp题,复杂度是 \(O(n^3) \sim O(1)\) 。当然如果只询问 \([1,n]\) ,那就是线性dp了,复杂度 \(O(n)\)。
设 \(f_{l,r,i,j}\) 代表考虑区间 \([l,r]\) ,左端点状态为 \(i(0/1)\) (是否向高位进位),右端点状态为 \(j(0/1)\) (是否从低位进位)时的操作次数最小值。
显然,两个区间合并成一个区间时,分割点位置是无后效性的。因为根据现有的状态,一个子区间状态的答案以及方案和包含它的区间的状态没有任何关系,可以推得无论分割点在哪,答案是固定的。
因此,状态转移方程为:
其中 \(mid\) 从 \([l,r]\) 任选一点即可。
但是现在要求能够修改,那就必须使用线段树维护区间的dp信息了,也就是动态dp,每个线段树区间 \([l,r]\) 维护一个矩阵 \(f[0/1][0/1]\) 即可。维护信息的过程是十分显然的,因为此区间dp和分割点无关,就直接按照线段树的修改合并查询就做完了。
另外,区间信息的单位元值不好找,可以直接合并时特判,或者合并前排除无效区间,都可以的。
时间复杂度 \(O((n+m)\log n)\)文章来源:https://www.toymoban.com/news/detail-431998.html
空间复杂度 \(O(n)\)文章来源地址https://www.toymoban.com/news/detail-431998.html
代码
#include <bits/stdc++.h>
using namespace std;
using ll = long long;
struct T {
array<array<int, 2>, 2> f = { (int)1e9,(int)1e9,(int)1e9,(int)1e9 };
friend T operator+(const T &a, const T &b) {
// 这里用特殊值判断无效区间
// 当然,也可以在递归的时候直接避免掉无效区间,而不是在合并时才判断
if (a.f[0][0] == 1e9) return b;
if (b.f[0][0] == 1e9) return a;
auto x = T();
//* 广义矩阵乘法(乘改加,加改取最大值)
for (auto i : { 0,1 })
for (auto j : { 0,1 })
for (auto k : { 0,1 })
x.f[i][j] = min(x.f[i][j], a.f[i][k] + b.f[k][j]);
return x;
}
};
struct F {
bool upd;
T operator()(const T &x) {
return{
upd,1,
1,!upd
};
}
};
template<class T, class F>
class SegmentTree {
int n;
vector<T> node;
void update(int rt, int l, int r, int x, F f) {
if (r < x || x < l) return;
if (l == r) return node[rt] = f(node[rt]), void();
int mid = l + r >> 1;
update(rt << 1, l, mid, x, f);
update(rt << 1 | 1, mid + 1, r, x, f);
node[rt] = node[rt << 1] + node[rt << 1 | 1];
}
T query(int rt, int l, int r, int x, int y) {
if (r < x || y < l) return T();
if (x <= l && r <= y) return node[rt];
int mid = l + r >> 1;
return query(rt << 1, l, mid, x, y) + query(rt << 1 | 1, mid + 1, r, x, y);
}
public:
SegmentTree(int _n = 0) { init(_n); }
SegmentTree(const vector<T> &src) { init(src); }
void init(int _n) {
n = _n;
node.assign(n << 2, T());
}
void init(const vector<T> &src) {
assert(src.size() >= 2);
init(src.size() - 1);
function<void(int, int, int)> build = [&](int rt, int l, int r) {
if (l == r) return node[rt] = src[l], void();
int mid = l + r >> 1;
build(rt << 1, l, mid);
build(rt << 1 | 1, mid + 1, r);
node[rt] = node[rt << 1] + node[rt << 1 | 1];
};
build(1, 1, n);
}
void update(int x, F f) { update(1, 1, n, x, f); }
T query(int x, int y) { return query(1, 1, n, x, y); }
};
int main() {
std::ios::sync_with_stdio(0), cin.tie(0), cout.tie(0);
int n;
cin >> n;
vector<T> a(n + 1);
for (int i = 1;i <= n;i++) {
char x;
cin >> x;
a[i] = {
x == '1',1,
1,x != '1'
};
}
SegmentTree<T, F> sgt(a);
int m;
cin >> m;
while (m--) {
int op;
cin >> op;
if (op == 1) {
int l, r;
cin >> l >> r;
cout << sgt.query(l, r).f[0][0] << '\n';
}
else {
int x;
bool val;
cin >> x >> val;
sgt.update(x, { val });
}
}
return 0;
}
到了这里,关于NC19469 01串的文章就介绍完了。如果您还想了解更多内容,请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章,希望大家以后多多支持TOY模板网!