前言
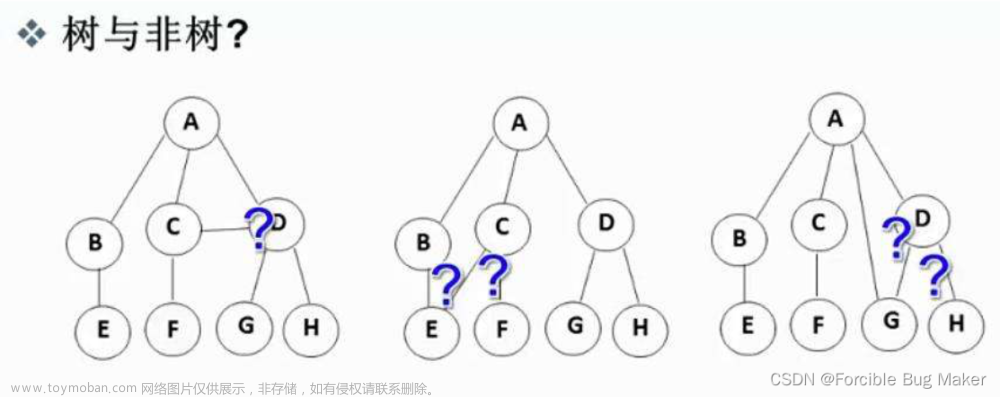
1.双亲表示法
由于每个节点都 只有一个父节点 ,所以我们可通过双亲来表示一棵树。具体方式通过数组的形式实现。
下标规律
- 根节点的下标为0
- 按照层序从上到下排序
- 每层从左向右递增
表示形式:
存储方式
- 二维数组
- 数据的列标为0,只需确定行标,即可锁定位置
- 根节点的父节点下标为 -1
- 列标为1存父节点,所存数据是父节点的行标
2.完全二叉树结论

完全二叉树孩子节点的计算
- 前提:节点的左右孩子均存在
- 设节点的下标为N
- 左孩子下标 = 2*N+1
- 右孩子下标 = 2*N+2
完全二叉树父节点的计算
- 前提:节点的父节点存在,且不为根节点
- 设节点的下标为N
- 父节点下标 = (N-1)/2
一.顺序结构
1.理念
- 顺序结构以数组形式存储
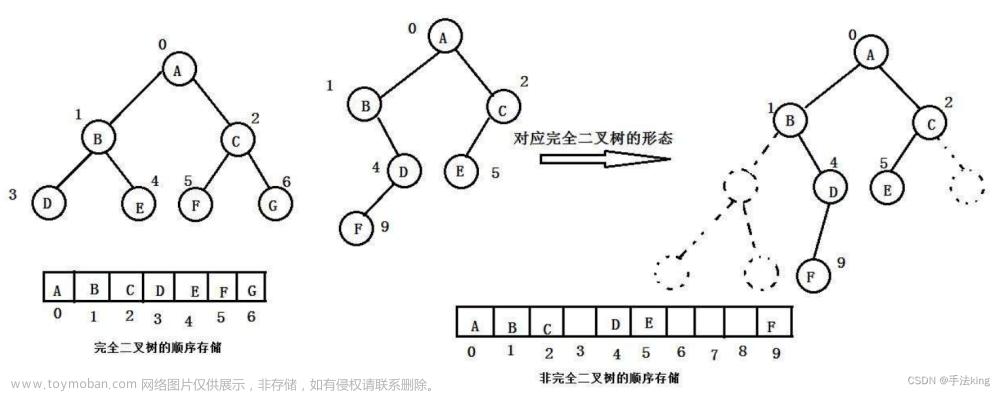
- 普通二叉树存储不便
- 堆是一种完全二叉树。适合以一维数组进行存储
注意:普通二叉树可以用一维数组存储,但空间浪费严重。
图示:
说明:深度越深,空间浪费越严重
补充
- 逻辑结构 : 人对数据的理解,而进行抽象的模型。
- 线性结构: 计算机对数据的理解,在计算机语言中的映射。
- 因此 :二叉树并不一定要用指针存储。
2.堆
概念:
如果有一个关键码1的集合K = {k1 ,k2 ,k3 ,…, },把它的所有元素按完全二叉树的顺序存储方式存储在一个一维数组中,并满足: ki<=k2*i+1且 ki<=k2*i+2 ( ki>=k2*i+1 且ki >=k2*i+2 ), i = 0,1,2…,则称为小堆(或大堆),此处的i是节点的下标。将根节点最大的堆叫做最大堆或大根堆,根节点最小的堆叫做最小堆或小根堆。
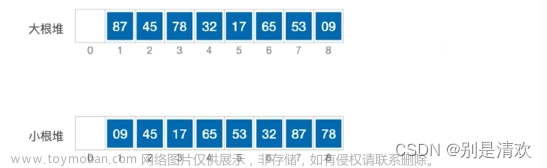
小根堆
- 一棵树的根节点都比其孩子节点要小
-
树可分为根和子树

大根堆
- 一棵树的根节点都比其孩子节点要大

3. 堆的实现
- 数组的形式——顺序表
//大根堆
typedef int HPDateType;
typedef struct Heap
{
HPDateType* arr;
int size;
int capacity;
}Heap;
-
关键思路:增和删数据
-
增数据:从栈底增,往上调
-
删数据:出栈顶,往下调
这里我实现的是:大根堆
1.初始化堆
- size设为0,表示当前数据元素的个数,也表示下一个数据的下标
- size设为-1,表示当前数据元素的下标
void HeapCreate(Heap* hp)
{
HPDateType* tmp = (HPDateType*)malloc(sizeof(HPDateType) * 4);
if (tmp == NULL)
{
perror("malloc fail");
exit(-1);
}
hp->arr = tmp;
hp->size = 0;
hp->capacity = 4;
}
辅助函数——交换元素
- 切记要传指针!
void Swap(HPDateType* arr, int child, int parent)
{
int tmp = arr[child];
arr[child] = arr[parent];
arr[parent] = tmp;
}
2.建堆——增加数据
- 从堆底进行增加,往上调数据
- 完全二叉树的孩子节点与父节点的关系,进行比较
- 孩子节点只与祖先进行比较,直到不比祖先大或者到根节点为止。
将1,9,3,5,7依次进堆
过程图:
向上调堆代码:
void AdjustUp(HPDateType* arr, int child)
{
int parent = (child - 1) / 2;
while (child > 0)
{
if (arr[parent] < arr[child])//不断与祖先比较
{
Swap(arr, child, parent);
child = parent;
parent = (child - 1) / 2;
}
else//遇到根节点或者不大于祖先就停止
{
break;
}
}
}
向堆里增加数据
void HeapPush(Heap* hp, HPDateType x)
{
int child = hp->size;
if (hp->size == hp->capacity)//判断是否需要扩容
{
HPDateType* tmp = (HPDateType*)realloc(hp->arr, \/*换行符*/
sizeof(HPDateType) * hp->capacity * 2);
if (tmp == NULL)
{
perror("realloc fail");
exit(-1);
}
hp->arr = tmp;
hp->capacity *= 2;
}
hp->arr[hp->size] = x;
AdjustUp(hp->arr, hp->size);
hp->size++;
}
3.删除数据
- 取的是堆顶的数据——一般我们需要最大的或者最小的
- 不应该把栈顶的数据往前移,这样会破坏堆的结构
- 一般把堆顶的数据与堆底的数据进行互换,然后对size减一,达到删除的效果
- 利用父节点与孩子节点的关系,表示左右孩子节点
- 从根节点开始到比其不大的左右孩子较大的或者比完数据结束
- 数据为0不能再删!
动态图解:
过程图解:
向下调整
void AdjustDown(HPDateType* arr, int parent, int size)
{
//假设左孩子为较大的孩子
int child = parent * 2 + 1;
while (child < size)//这里size是删过之后的数据个数,也是最后一个元素的下一个元素的下标
{
//先选出较大的孩子
if (child+1<size && arr[child + 1]>arr[child])
{
child++;
}
//错误示例:
// if (arr[child + 1]>arr[child]&&child+1<size)
// {
// child++;
// }
//说明:&&从左到右进行判断,这就好比:你犯错了还要弥补有什么用?
if (arr[child] > arr[parent])
{
Swap(arr, child, parent);
parent = child;
child = parent * 2 + 1;
}
else
{
break;
}
}
}
删除堆数据
void HeapPop(Heap* hp)
{
assert(hp);
assert(hp->size > 0);
Swap(hp->arr, hp->size-1, 0);
hp->size--;
AdjustDown(hp->arr, 0, hp->size);
}
4.取堆顶元素
- 有数据才能取
- 传入的指针不为空!
//取堆顶元素
HPDateType HeapTop(Heap* hp)
{
assert(hp);
assert(hp->size > 0);
return hp->arr[0];
}
4.堆排序
- 数组内数据为乱序——建堆
- 对数组内部元素进行排序——升序用大根堆/降序用小根堆
- 不使用额外的空间
向上调整(筛选法建堆)
- 从倒数第二层开始
- 每一层与其孩子节点较大的比较
- 直到不小于或到最后一层为止
动态图:
过程图:
时间复杂度——向上建堆
- 设高度为h
- 从最后一层开始到第一层结束——[h-1,1]
- 最后一层每个节点最多比1次,第一层每个节点最多比h-1次
| 高度 | 最多比较的次数 | 节点个数 |
|---|---|---|
| 1 | h-1 | 20 |
| 2 | h-2 | 21 |
| …… | …… | …… |
| h-1 | 1 | 2h-2 |
总次数
- 设总共比较T(N)次,二叉树节点总数为N
- 所用方法:错位相减
- 2*T(N)= 21 *(h-1)+22 *(h-2)+……+2h-2 *2+2h-1 *1
- T(N)= 20 *(h-1)+21 *(h-2)+……+ 2h-2 *1
- 第二个式子减去第一个式子。
- 得到:T(N)= -20(h-1)+21 +22+……+2h-2 +2h-1
- 整理得:T(N) = 20+21 +22+……+2h-1 +2h-1 - h
- 根据等比数列前n项和:S=a
1(1-qn)/1-q,a1为首项,q为等比 - 此处q=2,a
1=1,代入公式 - 因此:T(N)=2h -1 - h
- 又因为节点个数 N =2h - 1(满二叉树)
- 所以T(N)=N-log2(N+1),当N无穷大时,后一项可忽略。
- 因此:时间复杂度为O(N),N是节点的个数
代码实现:
void AdjustDown(HPDateType* arr, int parent, int size)
{
//左孩子,假设左孩子为较大的孩子
int child = parent * 2 + 1;
while (child < size)
{
//先选出较大的孩子
if (child+1<size && arr[child + 1]>arr[child])
{
child++;
}
if (arr[child] > arr[parent])
{
Swap(arr, child, parent);//上文有
parent = child;
child = parent * 2 + 1;
}
else
{
break;
}
}
}
void HeapCreat(int* arr, int size)
{
//向下调整
//((size - 1) - 1) / 2 表示倒数第二层的倒数第一个节点
/*(size-1)是最后一个节点的下标*/
for (int i = ((size - 1) - 1) / 2; i >= 0; i--)
{
AdjustDown(arr, i, size);
}
}
向下调整(筛选法建堆)
- 从第二层开始,到倒数第一层
- 每一层与其孩子节点较大的比较
- 直到不小于或到最后一层为止
图略~
时间复杂度——向下调整
- 设高度为h
- 从第2层开始到倒数第二层结束——[2,h-1]
- 最后一层每个节点最多比h-1次,第一层每个节点最多比1次
| 高度 | 最多比较的次数 | 节点个数 |
|---|---|---|
| 2 | 1 | 21 |
| 3 | 2 | 22 |
| …… | …… | …… |
| h | h-1 | 2h-1 |
- 方法:同上
- 结论:T(N)=2h *(h-2)+2
- 结合:节点个数 N =2h - 1(满二叉树)
- 整理得:T(N)=(N+1)*(log
2(N+1)-2)+2 - N趋于无穷大时,T(N)量级趋于N*log
2N - 因此:时间复杂度——O(n*log2N)
代码实现:
void AdjustUp(HPDateType* arr, int child)
{
int parent = (child - 1) / 2;
while (child > 0)
{
if (arr[parent] < arr[child])
{
Swap(arr, child, parent);
child = parent;
parent = (child - 1) / 2;
}
else
{
break;
}
}
}
void HeapCreat(int* arr, int size)
{
//向下调整
for (int i = 1; i < size; i++)
{
AdjustUpTwo(arr, i);
}
}
排序思路
- 将堆顶的数据与堆底的数据交换位置,不删除
- size 减去 1,减一是为了不动交换后的数据
- 调整堆的结构
动态图:
过程图:
代码实现:
void HeapSort(int* arr, int size)
{
//第一步调堆
//建大根堆——升序
//第一种:向上调整
//for (int i = 1; i < size; i++)
//{
// AdjustUp(arr, i);
//}
//第二种:向下调整
for (int i = ((size - 1) - 1) / 2; i >= 0; i--)
{
AdjustDown(arr, i, size);
}
int tmp = size - 1;//最后一个元素的下标
//时间复杂度:n*logn
while (tmp)
{
Swap(arr, tmp, 0);
tmp--;
AdjustDownTwo(arr, 0, tmp+1);//tmp+1指的是当前元素的个数
}
}
5.TopK问题
- 目的:从海量数据的取出前k大个的数/前K个小的数
- 堆大小:2GB左右
- 限制:2GB最多存大约2.5亿个整形(理想状况)
- 突破:硬盘有512GB的,大约可以存615亿个整形(理想状况),足够所需。
- 思路:将随机取k个数据,建立小根堆/大根堆,将硬盘里的数据不断的取出比较。
- 说明:取出前N个大的用小根堆,前K个最小的为边界,作为堆顶,比之大就进去,最后结果:堆顶的数据是前K个最小的。反之亦然。
我实现的是:从100000个数据中,取出前10个大的数。
-
在源文件的目录下创建一个文本文件

-
向文本文件中输出一百万个数字(不大于10000)
所用函数:
- fpoen
- 返回值:FILE*的指针
- 参数1:文件名——const char*
- 参数2:打开方式——这里是读(“r”)
- fprintf
- 返回值:输入的字符个数
- 参数1: 文件指针——FILE*
- 参数2:输入的字符串——const char*
- 参数3: 可变参数列表——数据
void DatasCreat()
{
FILE* p = fopen("datas.txt", "w");
if (p == NULL)
{
perror("fopen fail");
exit(-1);
}
srand((unsigned int)time(NULL));//设置随机数种子
int i = 0;
for (i = 0; i < 1000000; i++)
{
int ret = rand() % 10000;//产生1到9999的数字
fprintf(p, "%d\n", ret);
}
fclose(p);//使用完要关闭文件
}
- 修改10个文本中的数据使之大于10000

说明:使用过这个函数后要注释掉哦!再使用又会刷新文件数据,别问我怎么知道的。
- 取出文件中的前10个元素,建小根堆
这里先给出完整的函数声明和建小根堆的函数:
void DataSort(const char* fname, int k);
//小根堆
void AdjustUpTwo(HPDateType* arr, int child)
{
int parent = (child - 1) / 2;
while (child > 0)
{
if (arr[parent] > arr[child])
{
Swap(arr, child, parent);
child = parent;
parent = (child - 1) / 2;
}
else
{
break;
}
}
}
void HeapCreat(int* arr, int size)
{
//向下调整
for (int i = 1; i < size; i++)
{
AdjustUpTwo(arr, i);
}
}
- fscanf
- 读取结束标志:EOF
- 返回值:读取的元素个数
- 参数1:文件指针——FILE*
- 参数2: 读取的内容——const char*
- 参数3: 读到目标变量的地址
FILE* fp = fopen(fname, "r");
if (fp == NULL)
{
perror("fopen:fail");
}
int i = 0;
int arr[10] = { 0 };//也可以在堆上开辟
for (i = 0; i < 10; i++)
{
fscanf(fp, "%d", &arr[i]);
}
//建小根堆
HeapCreat(arr, sizeof(arr) / sizeof(arr[0]));
- 取出文件的数据,与堆顶元素进行比较
int ret = 0;
while (fscanf(fp, "%d", &ret)!=EOF)//文件的数据读完就结束
{
if (ret > arr[0])
{
arr[0] = ret;
AdjustDownTwo(arr, 0, sizeof(arr) / sizeof(arr[0]));
}
}
- 排升序——好看(可省略)
HeapSort(arr, 10);
- 打印数据
for (i = 0; i < 10; i++)
{
printf("arr[%d]:%d\n", i, arr[i]);
}
- 关闭文件
fclose(fp);
汇总TOPK排序的代码:
void DataSort(const char* fname, int k)
{
FILE* fp = fopen(fname, "r");
if (fp == NULL)
{
perror("fopen:fail");
}
int i = 0;
int arr[10] = { 0 };
for (i = 0; i < 10; i++)
{
fscanf(fp, "%d", &arr[i]);
}
//建小根堆
HeapCreat(arr, sizeof(arr) / sizeof(arr[0]));
int ret = 0;
while (fscanf(fp, "%d", &ret)!=EOF)
{
if (ret > arr[0])
{
arr[0] = ret;
AdjustDownTwo(arr, 0, sizeof(arr) / sizeof(arr[0]));
}
}
HeapSort(arr, 10);
for (i = 0; i < 10; i++)
{
printf("arr[%d]:%d\n", i, arr[i]);
}
fclose(fp);
}
void DatasCreat()
{
int i = 0;
FILE* p = fopen("datas.txt", "w");
if (p == NULL)
{
perror("fopen fail");
exit(-1);
}
srand((unsigned int)time(NULL));
for (i = 0; i < 1000000; i++)
{
int ret = rand() % 10000;
fprintf(p, "%d\n", ret);
}
fclose(p);
}
总结
希望对您有所帮助!文章来源:https://www.toymoban.com/news/detail-432165.html
-
数据元素中能起标识作用的数据项 ↩︎文章来源地址https://www.toymoban.com/news/detail-432165.html
到了这里,关于【数据结构】二叉树——顺序结构的文章就介绍完了。如果您还想了解更多内容,请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章,希望大家以后多多支持TOY模板网!