最近事多,好久没更新了,随便写写(Ctrl+V)点
一、超图定义
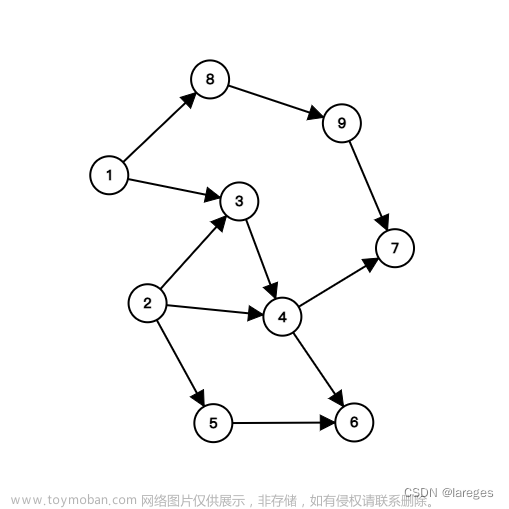
通常图论中的图,一条edge只能连接2个vertex,在超图中,不限量
如何理解呢,就用我正在做的KT问题来看:7道题目-7个顶点;4种概念-4条超边,其中第1,2,3题都是考察概念1的,则构建一个包含了这仨的超边,以此类推。。。总的来说,超图的建立是基于超边的建立,而超边的建立则是基于我们对节点之间关系的先验条件来实现的。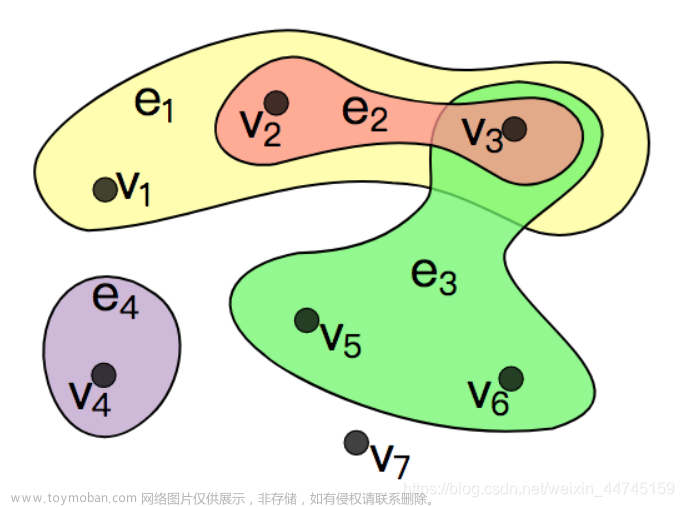
二、超图学习
1.表示
G=(V,E)是我们很熟悉的图的符号表示,这也同样适用于超图,我们可以用|V|*|E| 的 关联矩阵H表示,行代表了不同的节点,列代表了不同的超边: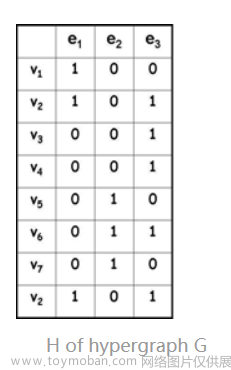
矩阵中每个元素的值可以由如下的关系式进行赋值:
同时,超图还有一种三元组的表示,G=(V,E,W),W是超边的权重集,即基于特定问题来对每条超边进行赋值,以此建立weighted hypergraph。
先讲两个度的概念
顶点的度d(v):定义为包含该到的边的个数,在超图中,表示为: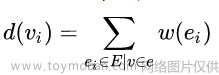
在基于上面提到的超图矩阵H,我们可以得到顶点的度的另一种定义: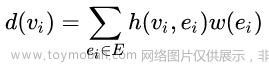
超边的度δ(e):定义为超边上包含的顶点的数目,表示为: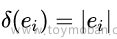
同样,超边的另一种定义: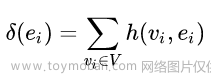
用对角矩阵Dv和De来表示节点、超边的degree矩阵,其中对角线上的元素就是每个节点/超边的degree即 d(v)或 δ(e)
设对角矩阵W表示超边的weight矩阵,其中对角线上的元素表示每条超边的weight即 w(e)。超图G的邻接矩阵(adjacent matrix)A定义为: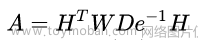
邻接矩阵表示了每个节点之间的相邻关系,其中每个元素的值可以表示为: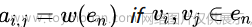
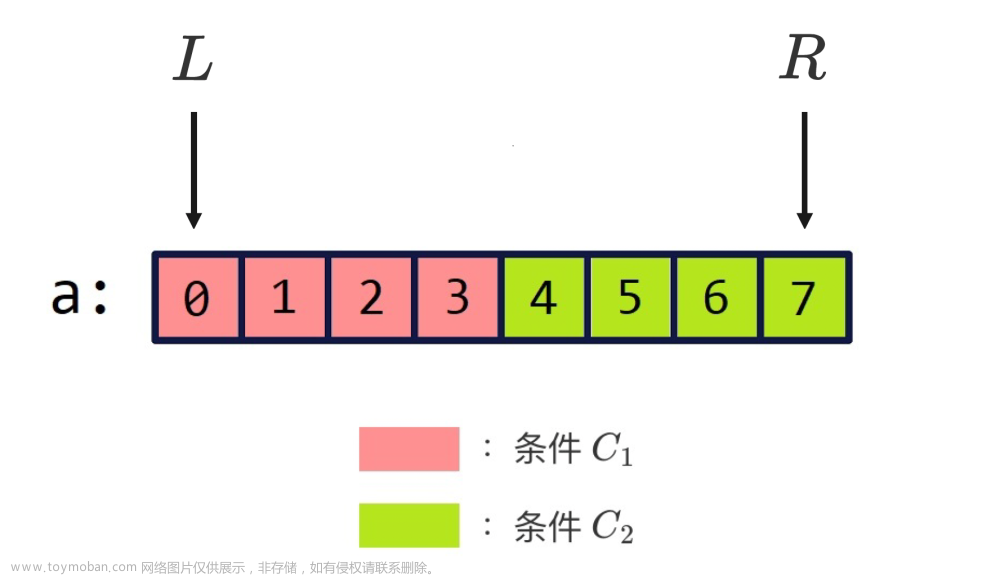
2.超图剪切
对于某个节点子集S∈V,超图剪切(cut)的含义是,对于超图G(V,E,W),我们要找到一个剪切方式,将 V 割为两个互补子集S和Sc 。假如超边e同时包含有S和Sc中的节点,我们则说它是一个剪切。文章来源:https://www.toymoban.com/news/detail-432269.html
超纲了,有需要再更新这块。。。文章来源地址https://www.toymoban.com/news/detail-432269.html
到了这里,关于超图(HyperGraph)学习,看这一篇就够了的文章就介绍完了。如果您还想了解更多内容,请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章,希望大家以后多多支持TOY模板网!