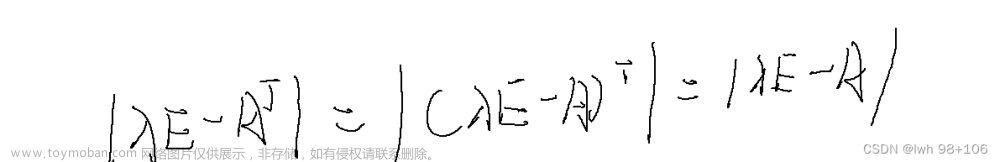对于向量 a = [ a 1 , a 2 , a 3 ] \mathbf a = [a_1,a_2,a_3] a=[a1,a2,a3], 其反对称矩阵为 a ^ = [ a × ] = [ 0 − a 3 a 2 a 3 0 − a 1 − a 2 a 1 0 ] \mathbf a\hat{}= [\mathbf a \times] = \begin{bmatrix}0 & -a_3 & a_2 \\ a_3&0&-a_1 \\ -a_2 &a_1 &0 \end{bmatrix} a^=[a×]= 0a3−a2−a30a1a2−a10
-
对于反对称矩阵 a × a \times a×,存在反交换性 :
a × = − [ a × ] T \mathbf a \times = - [\mathbf a \times ]^T a×=−[a×]T -
叉乘顺序互换,叉乘结果大小不变,方向相反
[ a × ] b = − [ b × ] a [\mathbf a \times] \mathbf b= - [\mathbf b \times] \mathbf a [a×]b=−[b×]a
a T [ b × ] = − b T [ a × ] \mathbf a^T [\mathbf b\times] = - \mathbf b^T [a\times] aT[b×]=−bT[a×] -
反对称矩阵相加
[ a × ] + [ b × ] = [ a + b ] × [\mathbf a\times] + [\mathbf b\times] = [\mathbf a+\mathbf b]\times [a×]+[b×]=[a+b]× -
标量点乘反对称矩阵
c ⋅ [ a × ] = [ c a × ] c \cdot [\mathbf a\times]=[c\mathbf a\times] c⋅[a×]=[ca×] -
向量与自己叉乘等于0向量
[ a × ] a = 0 [\mathbf a \times] \mathbf a= \mathbf 0 [a×]a=0 -
对于旋转矩阵R,存在:
[ R a × ] = R [ a × ] R [\mathbf R\mathbf a\times]=\mathbf R[\mathbf a\times] \mathbf R [Ra×]=R[a×]R
R ( [ a × ] b ) = [ R a × ] ( R b ) \mathbf R([\mathbf a\times] \mathbf b)=[\mathbf R\mathbf a\times] (\mathbf R\mathbf b) R([a×]b)=[Ra×](Rb) -
混合积
a ⋅ ( b × c ) = b ⋅ ( c × a ) = c ⋅ ( a × b ) \mathbf a\cdot (\mathbf b\times \mathbf c)= \mathbf b\cdot (\mathbf c\times \mathbf a)=\mathbf c\cdot (\mathbf a\times \mathbf b) a⋅(b×c)=b⋅(c×a)=c⋅(a×b) -
向量三重积
a × ( b × c ) = b ( a ⋅ c ) − c ( a ⋅ b ) \mathbf a\times (\mathbf b\times \mathbf c )= \mathbf b(\mathbf a\cdot \mathbf c)-\mathbf c(\mathbf a\cdot \mathbf b) a×(b×c)=b(a⋅c)−c(a⋅b)
[ a × ] [ b × ] = b a T − a T b I 3 [\mathbf a\times][ \mathbf b\times] = \mathbf b\mathbf a^T-\mathbf a^T\mathbf b\mathbf I_3 [a×][b×]=baT−aTbI3 -
二次幂公式
[ a × ] [ a × ] = a a T − ∣ ∣ a ∣ ∣ 2 2 I 3 [\mathbf a\times][ \mathbf a\times] = \mathbf a\mathbf a^T-||\mathbf a||^2_2I_3 [a×][a×]=aaT−∣∣a∣∣22I3 -
当 a \mathbf a a不为零向量时
a × \mathbf a\times a×的秩为2,必有一维零空间,且 a \mathbf a a是其中的一个解文章来源:https://www.toymoban.com/news/detail-432307.html
参考 :https://zhuanlan.zhihu.com/p/435306687文章来源地址https://www.toymoban.com/news/detail-432307.html
到了这里,关于反对称矩阵的性质的文章就介绍完了。如果您还想了解更多内容,请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章,希望大家以后多多支持TOY模板网!