首先我们定义一般形式的求解x的优化问题:
- 表示优化的目标函数,上述为最小优化,实际上最大优化可以改写为的形式
- 表示第i个不等式约束
- 表示等式约束
1. Lagrange对偶问题
上述优化问题的拉格朗日Lagrange对偶法求解,是将上述带约束的目标优化问题改写为如下无约束的Lagrange函数式子。
上述Lagrange函数式子存在如下对偶函数,其是Lagrange函数关于取最小值,即:
对偶函数是关于的函数,很显然其是原来Lagrange函数式子的下界,假设优化问题存在最优解,当时,此时存在最优目标大于对偶函数。
Lagrange对偶法即是通过最大化原问题Lagrange对偶函数,从而逼近原问题的下界来求解原问题最优解,因为的参数远小于原问题的求解参数,因此转换为对偶问题后,求解更为简单。
2. 强弱对偶性
接下来的问题是通过对偶函数得到下界同原问题的最优解之间的差距是多少?当对偶函数得到下界同原问题的最优解相等时,称之为强对偶性,反之称为弱对偶性。而这个差值称之为最优对偶间距。
Slater约束准则给出为强对偶性成立的条件:
- 原问题是凸问题
- 存在内点使得所有的不等式约束严格成立即,如果是仿射不等式时取等于也是可行的。
3. 如何转换为对偶函数
因为对偶函数是Lagrange函数关于取最小值,假设是关于x的凸函数,且存在关于x的最小值,此时存在使得关于x的偏导数为0,则存在对偶函数为。
假设为对偶函数为也是关于可导,此时最优值存在
此外最优值要使对偶函数存在最大值,由于,因此:
上述五个条件构成了在Slater约束准则下求解优化问题最优解存在的KKT条件:
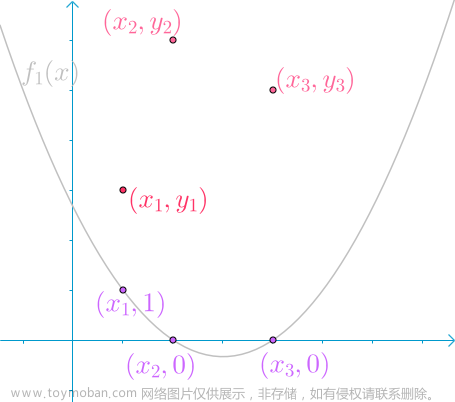
例子1:线性规划问题
首先我们定义一个一般性的线性规划问题,其中x是表示求解向量,该问题可解是指存在唯一解。
Lagrange函数式子表示为:
Lagrange函数仅当时,才是有界的,此时对偶函数为,否则为负无穷,因此原问题可以转换为求解对偶问题的最大值,此时Slater约束准则,对偶问题的解也是原问题的最优解。
例子2:最小二乘法
考虑以下问题:
Lagrange函数式子表示为:
Lagrange函数关于x是二阶可导的凸函数,存在最小值的解:
此时对偶函数为下式,此时原问题被转换为一个无约束的对偶问题的求解。
4. 最优问题的转换
接下来我们考虑更为通用的优化问题形式,之前讨论了不等式约束中的大于和小于可以通过变换符号进行调整,实际上我们可以通过新增求解变量将不等式约束转换为等式约束:
文章来源:https://www.toymoban.com/news/detail-432901.html
结合上述对偶问题的转换,我们可以将通用的优化问题形式转换为等式约束问题,甚至无约束的问题,下一篇我们将介绍等式约束优化问题和无约束优化问题的通用求解方法。文章来源地址https://www.toymoban.com/news/detail-432901.html
到了这里,关于优化问题的拉格朗日Lagrange对偶法原理的文章就介绍完了。如果您还想了解更多内容,请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章,希望大家以后多多支持TOY模板网!