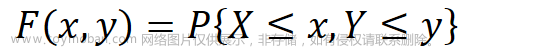边缘概率密度是二维随机变量中的重点内容， 经常作为一个重要的考点， 必须掌握。
一 定义
对二维随机变量(X, Y) ,分量X, 或者Y的概率密度称为 (X, Y)的边缘概率密度，简称边缘密度，记为 
或者 
。
边缘密度 或者 可由 二维随机变量的密度f(x, y)求出：
注意: 在实际题目中计算时，不可能代入到 , 因为那将导致算不出来。
而是根据实际区域来确定。
1.1 二维正态分布的边缘密度
若二维随机变是(X, Y) 服从二维正态分布N( 
), 则随机变量X与Y分别服从正态分布N(
), N(
). 边缘密度为
, 
二 结论
从定义看出, 求X的边缘密度
是对y求积分， 会带上dy, 因此要确定y的上下限， 注意确定上下限 时作一个垂直于x轴的箭头线，
求Y的边缘密度
是对x求积分， 会带上dx, 因此要确定x的上下限， 注意确定上下限 时作一个垂直于y轴的箭头线。
三 看例题
题1： 设二维连续型随机变量(X, Y)在区域D= {
, 
}上服从均匀分布， 求(X, Y)的边缘密度。
解 先画图
计算积分区域D的面积S = 
= 
所以(X, Y)的密度函数为 
关于X的边缘密度， 是对y积分， 先画图，并作箭头线垂直于X轴。
当 
时 , 
所以
,
关于Y的边缘密度， 是对x积分， 先画图， 并作箭头线垂直于Y轴。
当 
时， 
.
所以
~~~~~~
题2
设二维随机变量(X, Y) 的密度函数为
， 分布函数F(x, y), 则F(3, 2) =____________.
解：
对于二维随机变量， 密度为一个常数， 可以判定为均匀分布 ！！！
我们要明白： 分布函数的本质就是求概率。
对于此题， 先画图，图中画阴影区域占比即为F(3， 2)的值 ，
所以 F(3, 2) = 
题3
设二维连续型随机变量(X, Y)的密度为
， 求 P{X>}
解：
因为 密度函数不是常数， 所以绝不能用均匀分布的面积占比的方法。
先画图，
要求P{X>1/2}, 需要用二重积分解决，虽然求的概率只跟X有关。
积分区域D就是图中的三角形， 所以
P{X>} =
题4
设二维随机变量(X, Y)的概率密度为 
，且X与Y相互独立， 求P{X>Y}.
解： 此题，我们先画图， 此图只是用于辅助理解。
要求解P{X>Y}, 就是求解在积分区域D: X-Y>0下， 对密度函数进行二重积分。
题目4来源于教材P85第五题，原题目分别给出X, Y的概率密度，这是一个根据边缘密度函数的题目， 一定要掌握这类型题的解题方法：
先画图， 接着求出积分积分区域， 再作二重积分， 要特别注意积分上下限是怎么确定， 计算积分最后得出结果。文章来源：https://www.toymoban.com/news/detail-433235.html
这种方法也是一种套路， 一种路数，必须掌握。 因为下次我们看到的题可能是P{X<Y}.文章来源地址https://www.toymoban.com/news/detail-433235.html
四 结论
设X, Y都是非负的连续型随机变量，相互独立，则 P{X<Y} =
到了这里，关于概论_第3章_二维随机变量__边缘概率密度的文章就介绍完了。如果您还想了解更多内容，请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章，希望大家以后多多支持TOY模板网！
