多维时序 | MATLAB实现BP、SVM、LSSVM多变量时间序列负荷预测(考虑历史特征的影响,多指标、多图输出)
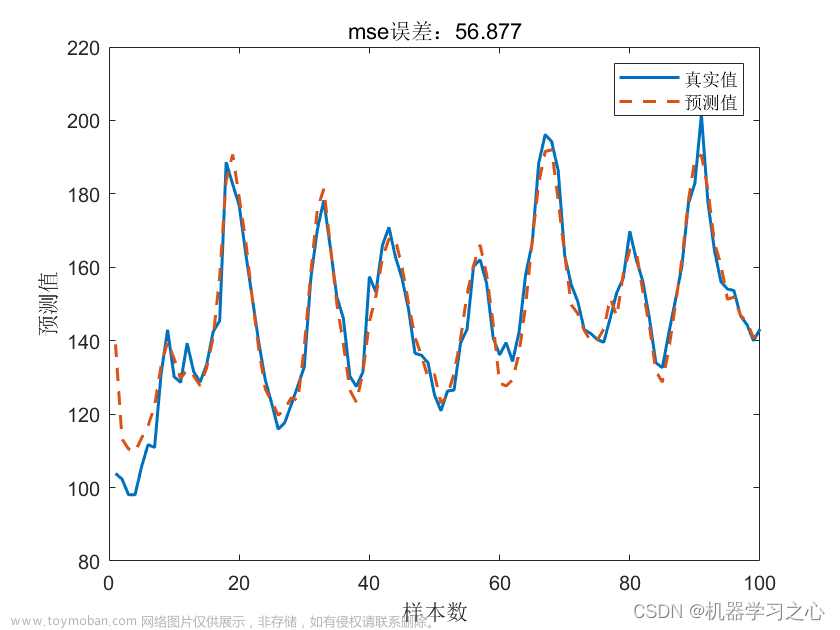
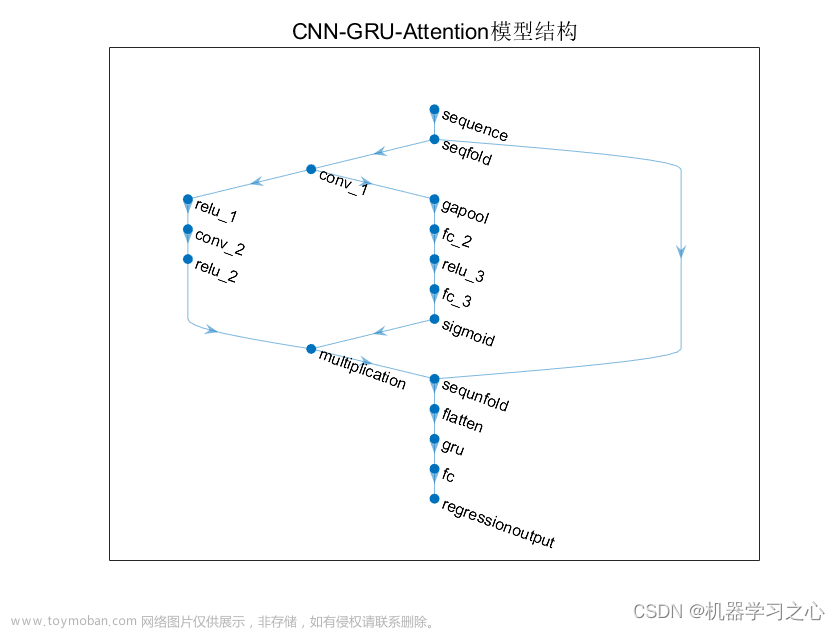
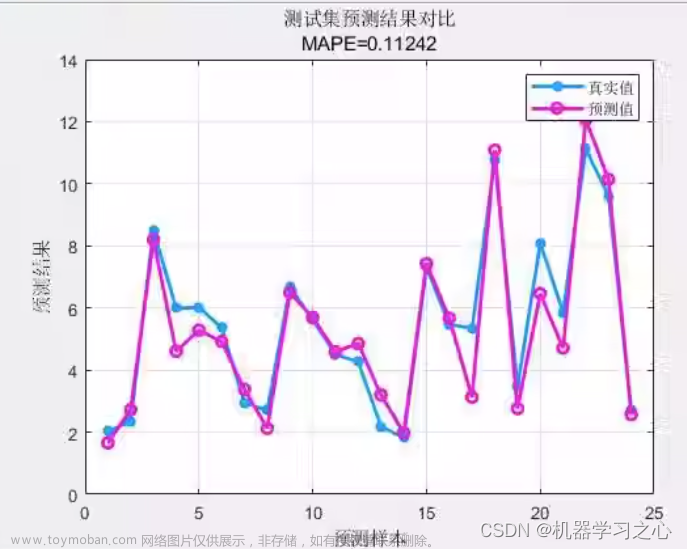
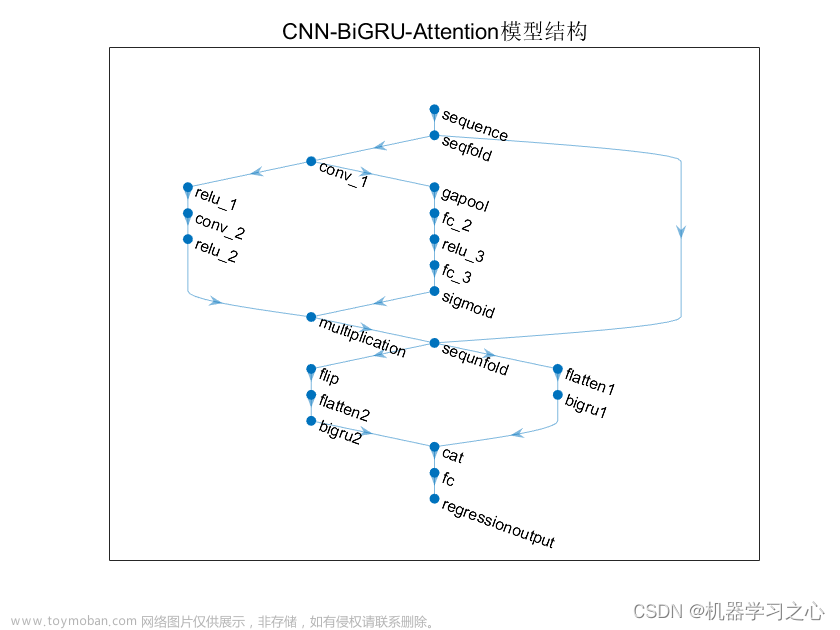
预测效果




基本介绍
多维时序 | MATLAB实现BP、SVM、LSSVM多变量时间序列负荷预测(考虑历史特征的影响,多指标、多图输出)。
1.Matlab实现BP、SVM、LSSVM多变量时间序列预测;
2.运行环境为Matlab2018b;
3.输入多个特征,输出单个变量,考虑历史特征的影响,多变量时间序列预测;
4.data为数据集,所有文件放在一个文件夹;
5.命令窗口输出R2、MSE、MAE、MAPE和MBE多指标评价;文章来源:https://www.toymoban.com/news/detail-433629.html
程序设计
- 完整程序和数据获取方式1:私信博主;
- 完整程序和数据获取方式2:同等价值程序兑换;
function cost = crossvalidatelssvm(model,Y, L, omega, estfct,combinefct)
% Estimate the model performance of a model with l-fold crossvalidation
%
%%%%%%%%%%%%%%%%%%%%%
% INTERNAL FUNCTION %
%%%%%%%%%%%%%%%%%%%%%
%
%if size(X,1)~=size(Y,1), error('X and Y have different number of datapoints'); end
nb_data = size(Y,1);
d = size(model.xtrain,2);
% LS-SVMlab
eval('model = initlssvm(model{:});',' ');
model.status = 'changed';
eval('L;','L=min(round(sqrt(size(model.xfull,1))),10);');
eval('estfct;','estfct=''mse'';');
eval('combinefct;','combinefct=''mean'';');
% Y is raw data, non preprocessed
py = Y;
[~,Y] = postlssvm(model,[],Y);
gams = model.gamcsa; try sig2s = model.kernel_parscsa; catch, sig2s = [];end
%initialize: no incremental memory allocation
costs = zeros(L,length(gams));
block_size = floor(nb_data/L);
% check whether there are more than one gamma or sigma
for j =1:numel(gams)
if strcmp(model.kernel_type,'RBF_kernel') || strcmp(model.kernel_type,'RBF4_kernel')
model = changelssvm(changelssvm(model,'gam',gams(j)),'kernel_pars',sig2s(j));
elseif strcmp(model.kernel_type,'lin_kernel')
model = changelssvm(model,'gam',gams(j));
elseif strcmp(model.kernel_type,'poly_kernel')
model = changelssvm(changelssvm(model,'gam',gams(j)),'kernel_pars',[sig2s(1,j);sig2s(2,j)]);
else
model = changelssvm(changelssvm(model,'gam',gams(j)),'kernel_pars',[sig2s(1,j);sig2s(2,j);sig2s(3,j)]);
end
% calculate matrix for LS-SVM once for the entire data
S = ones(nb_data,1);
Inb = eye(nb_data);
K = kernel_matrix2(omega,model.kernel_type,model.kernel_pars,d);
Atot = K+Inb./model.gam;
% Cholesky factor
try R = chol(Atot);
% Solve full system
q = R\(R'\[py S]);
p = q(:,2); q = q(:,1);
s = 1/sum(p);
bias = s*sum(q);
alpha = q - p*bias;
% Two expensive steps yet more efficient that using LINSOLVE on each fold
Ri = R\Inb;
C = Ri*Ri' - s*(p)*p';
catch %R = cholinc(sparse(Atot),1e-5);
A = [K+Inb./model.gam S; S' 0];
C = pinv(A);
alpha = C*[py;0];
%bias = alpha(nb_data+1);
alpha = alpha(1:nb_data);
end
% start loop over l validations
for l = 1:L,
% divide data in validation set and trainings data set
if l==L,
%%train = 1:block_size*(l-1); % not used
validation = block_size*(l-1)+1:nb_data;
else
%%train = [1:block_size*(l-1) block_size*l+1:nb_data]; % not used
validation = block_size*(l-1)+1:block_size*l;
end
% Submatrix of C to compute residuals for the l-th fold left out
Ckk = C(validation,validation);
% Solution of small linear system (block_size x block_size)
try % faster
Rkk = chol(Ckk+eps);
betak = Rkk\(Rkk'\alpha(validation));
catch
betak = Ckk\alpha(validation);
end
% latent outputs for validation
yh = py(validation) - betak;
[~,yh] = postlssvm(model,[],yh);
if ~(model.type(1)=='c')
costs(l,j) = feval(estfct,yh - Y(validation,:));
else
costs(l,j) = feval(estfct,Y(validation,:),sign(yh));
end
end
end
cost = feval(combinefct, costs);
学习总结
- 一些基本的思路和步骤来实现多变量时间序列预测。
- 数据预处理:首先需要对多变量时间序列数据进行预处理,包括数据清洗、缺失值处理、特征工程等。对于历史特征的影响,可以考虑加入滞后项或差分项等特征。
- 数据划分:将数据分为训练集和测试集,一般采用时间序列的划分方式,即前一部分数据作为训练集,后一部分数据作为测试集。
- BP神经网络实现:利用MATLAB中的函数实现BP神经网络,通过调整网络的参数和结构来优化训练效果。
- SVM实现:利用MATLAB中函数实现SVM模型,通过调整SVM的超参数来优化模型效果。
- LSSVM实现:利用MATLAB中的“trainlssvm”函数实现LSSVM模型,同样需要调整超参数来优化模型效果。
- 模型评估:通过对测试集的预测结果进行评估,可以使用常见的评估指标如均方误差、平均绝对误差、均方根误差等,来比较不同模型的预测效果。
- 以上是一个基本的多变量时间序列预测的实现步骤和思路,具体的实现细节需要根据数据和模型的具体情况进行调整。
参考资料
[1] https://blog.csdn.net/kjm13182345320/category_11799242.html?spm=1001.2014.3001.5482
[2] https://blog.csdn.net/kjm13182345320/article/details/124571691文章来源地址https://www.toymoban.com/news/detail-433629.html
到了这里,关于多维时序 | MATLAB实现BP、SVM、LSSVM多变量时间序列预测(考虑历史特征的影响,多指标、多图输出)的文章就介绍完了。如果您还想了解更多内容,请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章,希望大家以后多多支持TOY模板网!