欢迎关注公众号:sumsmile /专注图形学
起初,只是想弄清楚2D图像的频谱图的含义,没想到越肝越深,前后肝了一个多月。
接《傅里叶变换及应用python版(1)》,这篇主要讲代码,通过几个典型的案例,直观的理解傅里叶变换
代码参考教程:
https://www.bilibili.com/video/BV1X8411a74G/?vd_source=7f6a092b306354c9eef8f3cd5bd5307d
离散傅里叶变换的重要概念
- 实信号的对称性
实数信号经过傅里叶变换得到的频域图像,是关于原点对称的(一维信号关于y轴对称)

- 离散信号的周期化
连续信号进行采样,在频域有周期延拓的现象

意思是,原始信号的频域只有中间蓝色图像,但是采集完经过傅里叶变换得到的频率是呈周期性重复
- 奈奎斯特采样定理、混叠
用频率f对信号signal进行采样,最多只能只能采集f/2频率的信号。比如:采样频率为10hz,即每秒采样10次,那最多只能对5hz的信号进行采样,超过5hz的信号,采样出来的数据是错误的

如果采样频率较小,而采样后的是周期化的频率,那么最后得到的频率在边界处有交叉混叠,即高频信号是错误的,如果是图像就会变的模糊。这一条要理解好需要花点时间,我还没找到讲的非常好的资料,建议读者先假设这是对的,不要在这block。

这些定理、特征可以参考(1)里推荐的资料,里面有推导,如果不好理解,你也可以认为这是计算证明的结果,不用刻意非要从物理的角度解释这些现象。
上代码~~
代码案例
安装好Python环境,3.x以上均可
import 常用的库
import numpy as np
import math
import matplotlib.pyplot as plt
import scipy.fftpack
import random
from mpl_toolkits.mplot3d import Axes3D
example-1 离散傅里叶变换
手动创建一个信号,包含两个基础三角函数
signal=2.5sin(2π * 4 * t)+1.5sin(2π * 6.5 * t)
通过傅里叶变换,提取出两个频率


可以看到,对手动生成的信号,正确的计算出频谱图,除了4hz、6.5hz,其他频率对应的幅值都为0
## 循环的方式实现DTFT(离散傅里叶变换)
# 手动创建一个信号,由两个sin函数组合,频率幅值分别是[4, 2.5]、[6.5, 1.5]
srate = 1000 # 采样率,hz,即每秒采样1000次
time = np.arange(0.,2.,1/srate) # 时间序列对2秒按0.1步长分割,x轴坐标[0.1, 0.2, 0.3, ....2]
pnts = len(time) # 绘制的点等于时间序列的长度
signal = 2.5 * np.sin( 2*np.pi*4*time ) + 1.5 * np.sin( 2*np.pi*6.5*time )
# 准备傅里叶变换的数据
fourTime = np.array(range(pnts))/pnts #傅里叶变换的时间序列,0/N, 1/N, 2/N, 3/N...N-1/N
fCoefs = np.zeros((len(signal)),dtype=complex) #即Ck,每个三角函数的系数,每个频率分量的特征(幅值、频率、相位)
# 先绘制signal
plt.plot(time,signal)
plt.xlabel('Time (sec.)'), plt.ylabel('Amplitude (a.u.)')
plt.title('Signal')
plt.show()
# range(pnts):[0,1,2,3,....N]
# 我们并不知道原始的信号由哪些频率分量,那我们穷举,通过傅里叶变换,把很大范围的频率都求出来
# 不为0的信号分量就是有效成分
for fi in range(pnts):
# 创建复数形式的三角函数 exp(-i2π * k * t),我习惯称为基
csw = np.exp( -1j*2*np.pi*fi*fourTime )
# 将原信号和该基相乘求和,除以pnts,是因为在离散傅里叶变换中,基的模不为1,为了归一化处理
fCoefs[fi] = np.sum( np.multiply(signal,csw) ) / pnts
# fcoefs是复数形式,取模,得到幅值,* 2后面会解释,是因为信号的频率关于y轴对称,但我们只求了正频率
# 如果不能理解为啥 * 2 ,可以先放一边,或者就记住也行,不影响对整体的理解
ampls = 2*np.abs(fCoefs)
# 生成频率值,用于x轴,srate/2表示,只取采样频率的一半,根据奈奎斯特采样定律,只有一半的采样频率是正确的
hz = np.linspace(0,srate/2,int(math.floor(pnts/2.)+1))
# 在x-y平面绘制频谱,
plt.stem(hz,ampls[range(len(hz))])
plt.xlabel('Frequency (Hz)'), plt.ylabel('Amplitude (a.u.)')
plt.xlim(0,10)
plt.show()
example-2 离散傅里叶逆变换
通过给定的频率,还原出原始的信号
- 先创建一个信号
# 创建信号
srate = 1000 # 采样频率 hz
time = np.arange(0,2*srate)/srate # 采样时间为2秒,每1/1000秒采样一次,共采样2000次,两个周期
pnts = len(time) # 采样的点数
# 用两个基本三角函数合成信号 频率4 + 频率6.5
signal = 2.5 * np.sin( 2*np.pi*4*time ) + \
1.5 * np.sin( 2*np.pi*6.5*time )
# 绘制信号
plt.plot(time,signal,'k')
plt.xlabel('Time (s)')
plt.ylabel('Amplitude')
plt.title('Time domain')
plt.show()

- 计算傅里叶变换
# 前面讲过了,计算傅里叶变换因子,不再过多注释了
fourTime = np.arange(0,pnts)/pnts
fCoefs = np.zeros(len(signal),dtype=complex)
for fi in range(pnts):
csw = np.exp( -1j*2*np.pi*fi*fourTime )
fCoefs[fi] = sum( signal*csw ) / pnts
# 计算每个频率的幅值
ampls = 2*abs(fCoefs)
- 绘制频谱图、相位谱、傅里叶逆变换重建信号
# compute frequencies vector
hz = np.linspace(0,srate/2,int(np.floor(pnts/2)+1))
# plot amplitude
plt.stem(hz,ampls[:len(hz)],'ks-')
# make plot look a bit nicer
plt.xlim([0,10])
plt.ylim([-.01,3])
plt.xlabel('Frequency (Hz)')
plt.ylabel('Amplitude (a.u.)')
plt.title('Amplitude spectrum')
plt.show()
# plot angles
plt.stem(hz,np.angle(fCoefs[:len(hz)]),'ks-')
# make plot look a bit nicer
plt.xlim([0,10])
plt.ylim([-np.pi,np.pi])
plt.xlabel('Frequency (Hz)')
plt.ylabel('Phase (rad.)')
plt.title('Phase spectrum')
plt.show()
# finally, plot reconstructed time series on top of original time series
reconTS = np.real(scipy.fftpack.ifft( fCoefs ))*pnts
plt.plot(time,signal,'k',label='Original')
plt.plot(time[::3],reconTS[::3],'r.',label='Reconstructed')
plt.legend()
plt.show()



红色的点是重建的信号,可以看到,几乎一模一样的贴合
上面用python库处理傅里叶逆变换,作为对比组。下面手动计算一遍。
example-3 手动计算傅里叶逆变换
创建信号的流程一样
srate = 1000 # hz
time = np.arange(0,2.,1/srate) # time vector in seconds
pnts = len(time) # number of time points
signal = 2.5 * np.sin( 2*np.pi*4*time ) + 1.5 * np.sin( 2*np.pi*6.5*time )
fourTime = np.array(np.arange(0,pnts))/pnts
fCoefs = np.zeros(len(signal),dtype=complex)
for fi in range(0,pnts):
csw = np.exp( -1j*2*np.pi*fi*fourTime )
fCoefs[fi] = np.sum( np.multiply(signal,csw) )
ampls = np.abs(fCoefs) / pnts
ampls[range(1,len(ampls))] = 2*ampls[range(1,len(ampls))]
hz = np.linspace(0,srate/2,num=math.floor(pnts/2)+1)
plt.stem(hz,ampls[range(0,len(hz))])
plt.xlim([0,10])
plt.show()
手动计算傅里叶逆变换,这里我没太弄明白,为啥重建的时候不用乘以2
## 傅里叶逆变换
# 初始化重建的信号
reconSignal = np.zeros(len(signal));
for fi in range(0,pnts):
# 计算每个信号分量的离散值,注意,csw是一个长度为len(fourTime)的数组
csw = fCoefs[fi] * np.exp( 1j*2*np.pi*fi*fourTime )
# 所有信号加和
reconSignal = reconSignal + csw
# 除以 N. 注意重建的时候,不用* 2(这里我没太深究,为啥重建的时候不用乘以2)
reconSignal = reconSignal/pnts
plt.plot(time[::4],np.real(reconSignal)[::4],'r.',label='reconstructed')
plt.plot(time,signal,label='original')
plt.legend()
plt.show()

手动计算的效果也是一样的
example-4 直流分量处理(DC coefficient)
前面处理的都是单纯的三角函数相加的信号,实际上有的信号里有固定值的信号成分
比如:
signal = 1.5 + 2.5*sin( 2π * 4 * t)
多了一个固定值1.5,将整个sin函数沿y轴上移了1.5,这个1.5因为没有周期,也叫直流分量

前面讲过,经过傅里叶变换计算出来的因子前面要乘以2,才是真实的信号频率,这是因为信号具有对称性,所以要加上"负信号"那部分才对应原始信号。
注意:这个乘以2,不包括直流分量

看上图,一个信号经过DTFT得到频谱,其他的信号均是对称的,唯有"0"处的信号只有一份,所以对频率为"0"的信号要特殊处理。
# 创建信号
srate = 1000 # hz
time = np.arange(0.,2.,1/srate) # 生成时间序列
pnts = len(time) # 时间点数量
# 生成频率为4,幅值为2.5的信号,再加上直流分量1.5
signal = 1.5 + 2.5*np.sin( 2*np.pi*4*time )
# 准备傅里叶变换的参数
fourTime = np.array(range(pnts))/pnts
fCoefs = np.zeros(len(signal),dtype=complex)
for fi in range(pnts):
# 对每个频率生成基向量信号
csw = np.exp( -1j*2*np.pi*fi*fourTime )
# 原信号与基向量点乘,求得每个频率对应傅里叶因子
fCoefs[fi] = np.sum( np.multiply(signal,csw) )
# 之前的代码里,笼统的都会 * 2 求得傅里叶因子,但是遇到包含直流分量的信号,是不完全正确的
# ampls = 2*np.abs(fCoefs/pnts);
# 计算所有傅里叶因子的幅值(还没有 * 2,是不正确的)
ampls = np.abs(fCoefs/pnts);
# 除开第0个值(直流分量)不做额外处理,其他分量都 * 2
ampls[1:len(hz)] = 2*ampls[1:len(hz)]
# 生成频谱图的x轴
hz = np.linspace(0,srate/2,num=int(math.floor(pnts/2.)+1))
# 绘制原信号
plt.plot(time,signal,'k')
plt.xlabel('Time (s)')
plt.ylabel('Amplitude')
plt.title('Time domain')
plt.show()
# 绘制频谱图
plt.stem(hz,ampls[0:len(hz)])
plt.xlim(-.1,10)
plt.xlabel('Frequency (Hz)'), plt.ylabel('Amplitude (a.u.)')
plt.show()

可以看到,频谱图和原信号的各个分量都对的上了。如果直流分量的频率也乘以2,则"0"对应的就不是1.5了,变成3了。
这个细节有点绕,如果你不能太理解,建议你暂时记住,直流分量信号需要特殊处理。直流分量代表整个信号的品均值。
参考:如何理解图像傅里叶变换的频谱图
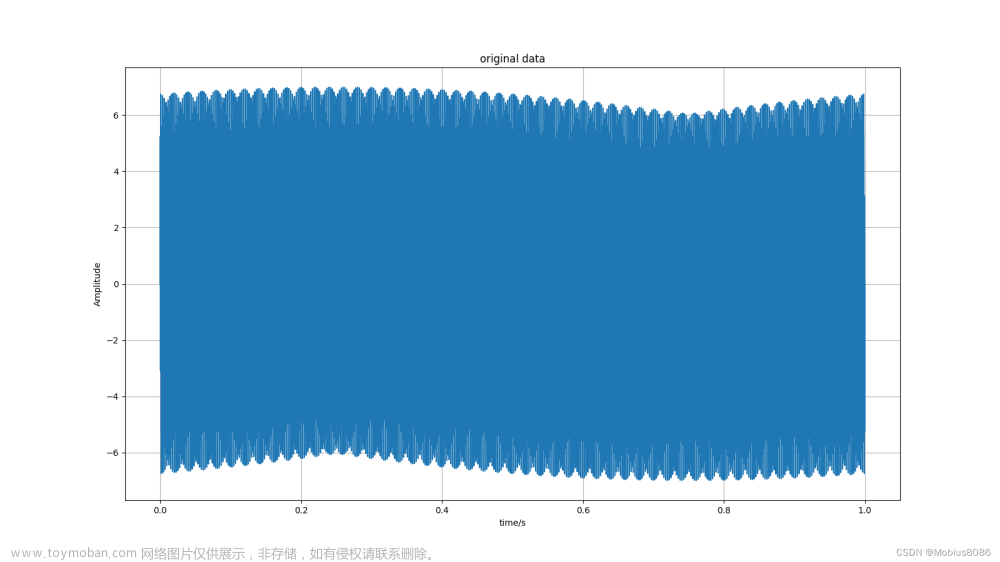
example-5 过滤信号的实现
给出下面信号,过滤掉频率为10的信号
signal = sin(2π * 4 * t) +sin(2π * 10 * t)
原始信号的图像:
频谱图:
过滤掉频率为10的信号,仅保留频率为5的信号
完整代码如下:
import numpy as np
import math
import matplotlib.pyplot as plt
import pylab as pl
from IPython import display
import time as ttime
import random
from mpl_toolkits.mplot3d import Axes3D
## 带通过滤
# 参数
srate = 1000
time = np.arange(0,2-1/srate,1/srate)
pnts = len(time)
# 原始信号 signal
signal = np.sin(2*np.pi*4*time) + np.sin(2*np.pi*10*time)
# 傅里叶变换
fourTime = np.array(np.arange(0,pnts))/pnts
fCoefs = np.zeros(len(signal),dtype=complex) #傅里叶变换的因子是负数
for fi in range(0,pnts):
# 创建复数形式的基信号
csw = np.exp( -1j*2*np.pi*fi*fourTime )
# 点乘计算每个基信号的傅里叶因子,记得/pnts
fCoefs[fi] = np.sum( np.multiply(signal,csw) )/pnts
# 生成x轴,单位为hz
hz = np.linspace(0,srate/2,int(np.floor(pnts/2.0)+1))
# 找到10 hz附近的信号
# argmin,指的事找到一个数组里值最小的数的索引
# 这里要注意,因为是浮点计算,真实计算过程中,不一定是10,可能是10.001
freqidx = np.argmin(np.abs(hz-10))
# 设置对应的频率为0
fCoefsMod = list(fCoefs)
fCoefsMod[freqidx] = 0
# 注意,根据奈奎斯特采样定律,采样频率f最多只能采样f/2的频率,但是经过傅里叶变换实际会得到1/f个频率(一个周期的数据)
# 另一半高频分量实际上 f/2的重复,所以实际上是去掉两个频率
fCoefsMod[len(fCoefsMod)-freqidx] = 0
# 计算逆变换
reconMod = np.zeros(len(signal),dtype=complex)
for fi in range(0,pnts):
csw = fCoefsMod[fi] * np.exp( 1j*2*np.pi*fi*fourTime )
reconMod = reconMod + csw
# 绘制原始信号
plt.plot(time,signal)
plt.title('Original signal, time domain')
plt.show()
# 绘制原始频谱
plt.stem(hz,2*np.abs(fCoefs[0:len(hz)]))
plt.xlim([0,25])
plt.title('Original signal, frequency domain')
plt.show()
# 绘制过滤后的信号
plt.plot(time,np.real(reconMod))
plt.title('Band-stop filtered signal, time domain')
plt.show()
注意:
注意,根据奈奎斯特采样定律,采样频率f最多只能采样f/2个有效频率,f=1000时,只有500个频率是有效的,后面一半频率数据是离散信号周期延拓造成的。
下面是原始信号经过傅里叶变换,完整的频谱(不包含负频率),可以看到有两组频率关于500对称。
所以实际上是去掉两个频率,一个是10,另一个是 (1000-10),它俩的幅值是一样的
example-6 快速傅里叶变换 fft
fft的推导有点麻烦,网上有很多资料,有兴趣可以自行查阅研究。建议初学者不要花太多时间耗在这。
下面的案例,主要对比fft 和手动实现的效率对比,可以看到fft比基于for循环的实现效率高两个数量级,如果信号的数据量更大,这个差异也会增大。
代码比较简单不做过多解释:
# create the signal
pnts = 1000
signal = np.random.randn(pnts)
# start the timer for "slow" Fourier transform
tic = timeit.default_timer()
# prepare the Fourier transform
fourTime = np.array(range(0,pnts))/pnts
fCoefs = np.zeros(len(signal),dtype=complex)
for fi in range(0,pnts):
csw = np.exp( -1j*2*np.pi*fi*fourTime )
fCoefs[fi] = np.sum( np.multiply(signal,csw) )
# end timer for slow Fourier transform
toc = timeit.default_timer()
t1 = toc-tic
# time the fast Fourier transform
tic = timeit.default_timer()
fCoefsF = scipy.fftpack.fft(signal)
toc = timeit.default_timer()
t2 = toc-tic
# and plot
plt.bar([1,2],[t1,t2])
plt.title('Computation times')
plt.ylabel('Time (sec.)')
plt.xticks([1,2], ['loop','FFT'])
plt.show()
print('t1:', t1, " t2: ", t2)
耗时对比:
for-loop: 0.045256367997353664
fft: 0.00010827200094354339

直观的看到,fft的实现,基本上不怎么耗时
后面我们都用fft来处理信号
2D傅里叶变换原理
穿插一点2D傅里叶变换的原理
公式:
从形式上看,将一维的变量升级到2维,
x ‾ \underline{x} x 对应1维傅里叶变换里的 time,在二维图像里表示x、y坐标
ξ ‾ \underline{\xi} ξ 对应1维傅里叶变换里的 k(频率),在二维图像里表示该频率是沿着某个方向
将向量展开可以写成:

以这张图为例

按3D的形式呈现(颜色深浅代表高度)

那么频率在x-y平面,会沿着任意方向伸展。
如果不好理解,可以按第二种方式理解:
一张图片如下:

每个方格表示一个像素颜色值,值越大颜色越深。
2D傅里叶变换可以理解为两次1D傅里叶变换,先沿着y轴变换一次,再沿着x轴变换一次。
沿着Y轴变换:
每列的第一个值表示该列进行1D傅里叶变换后得到的直流分量,即频率为0的值,常量信号
沿着X轴变换:
最后的结果如下,左上角是低频,其他三个角因为周期性,和左上角成对称关系,本质上也是低频。所以结果图中,中间是高频,四周是低频。
一般来说,低频的信号幅值大,组成一个信号的基本面,高频的信号幅值小,刻画细节、轮廓。
在很多领域,比如图像处理,会将四周的低频信号放到原点附近,高频信号放到四周

经过居中处理,对调频谱的四个象限

得到我们常见的图像频谱图

接着看代码
example-7 2D傅里叶变换1
实现下面的效果,不断改变三角波的方向,生成连续的动画,观察2d幅值频谱的变化,幅值频谱图上只有成对称的两个点,即只对应一个频率。
代码:
import numpy as np
import math
import matplotlib.pyplot as plt
import pylab as pl
from IPython import display
import time
import random
import scipy.fftpack
from mpl_toolkits.mplot3d import Axes3D
from scipy import signal
from scipy import interpolate
# 定义三角函数序列
sinefreq = np.linspace(.0001,.2,50) # arbitrary units
# 固定相位为π/4,
sinephas = np.pi/4
# sine wave initializations
# 生成一个x[-91, 91] y[-91, 91]的矩阵网格,网格的值分别沿x、y轴均匀增加
lims = [-91,91]
# meshgrid原理:https://wangyeming.github.io/2018/11/12/numpy-meshgrid/
[x,y] = np.meshgrid(range(lims[0],lims[1]),range(lims[0],lims[1]))
# 生成沿着角度sinephas梯度变化的矩阵,作为2d傅里叶变换的坐标序列
xp = x*np.cos(sinephas) + y*np.sin(sinephas)
# 动态更新画面10次,形成一个连续的动画
for si in range(0,10):
# 生成一张2D正弦波图片,正弦波的传播方向是xp的梯度方向,即sinephas角度,注意,图片y轴正方向朝下
img = np.sin( 2*np.pi*sinefreq[si]*xp )
# 获取该图片的傅里叶变换因子,即频率属性,并且进行shift操作,将低频移到中心,高频移到周围
imgX = scipy.fftpack.fftshift(scipy.fftpack.fft2(img))
# 获取幅值和相位
powr2 = np.abs(imgX)
phas2 = np.angle(imgX)
# 画出原始正弦波图
pl.cla() # 清除画布
plt.subplot2grid((1,2),(0,0))
plt.contourf(img)
# 绘制幅值频谱
plt.subplot2grid((2,2),(0,1))
plt.contourf(powr2)
plt.xlim([61,121])
plt.ylim([61,121])
# 绘制相位频谱
plt.subplot2grid((2,2),(1,1))
plt.contourf(phas2)
# 清除输出
display.clear_output(wait=True)
# 更新界面
display.display(pl.gcf())
# sleep 0.1秒
time.sleep(0.1)
example-8 2D傅里叶变换2
实现下面的效果,不断更改图片中圆形的位置,观察到,幅值频谱图保持不变,why?图中圆形的大小不变,仅改变相对坐标。
把圆形看成空间域的一段信号,这个信号的特征没有改变,只是改变"出场的时机",幅值频谱只和信号的形状有关,但是观察右下方的相位谱不断在变化,表示信号分量的初始角度持续在变

复用了example-7 的一段代码(网格梯度的生成)
# 用高斯函数模拟一个圆形
width = 20 # 高斯函数的宽度
centlocs = np.linspace(-80,80,50)
for si in range(0,len(centlocs)):
# create Gaussian
mx = x-centlocs[si]
my = y-20
# 以mx my 为中心,生成高斯函数
gaus2d = np.exp( -( mx**2 + my**2 ) / (2*width**2) )
img = np.zeros((len(gaus2d),len(gaus2d)))
# > 0.9的地方置为1,表示有颜色
img[gaus2d>.9] = 1
# 2D fft,获取幅值频谱和相位频谱
imgX = scipy.fftpack.fftshift(scipy.fftpack.fft2(img))
powr2 = np.abs(imgX)
phas2 = np.angle(imgX)
# 显示原图
pl.cla() # wipe the figure
plt.subplot2grid((1,2),(0,0))
plt.contourf(img)
# 展示幅值频谱
plt.subplot2grid((2,2),(0,1))
plt.contourf(powr2)
plt.xlim([61,121])
plt.ylim([61,121])
# 展示相位频谱
plt.subplot2grid((2,2),(1,1))
plt.contourf(phas2)
display.clear_output(wait=True)
display.display(pl.gcf())
time.sleep(.01)
example-8 图像滤波-模糊效果
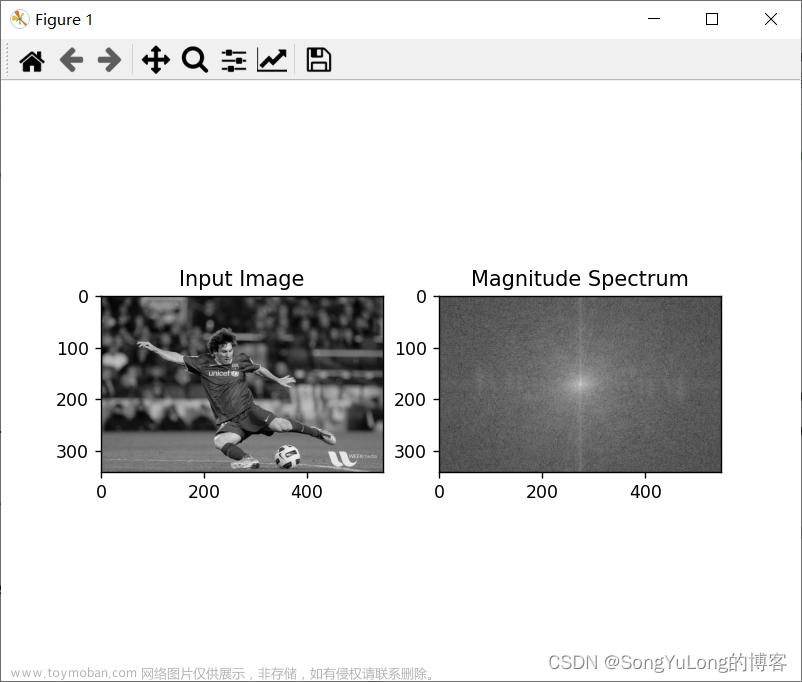
- 提取原图片的幅值频谱
- 在频域和一个过滤函数相乘(图片)
- 将得到的新的频谱图还原成空间域信号

# 加载图片图片
lenna = np.asarray( Image.open("Lenna.png") )
# 对RGB通道求均值 axis=2表示RGB通道
imgL = np.mean(lenna,axis=2)
# 绘制原图
plt.subplot2grid((2,2),(0,0))
plt.imshow(imgL,cmap=plt.cm.gray)
# plt.axis('off')
plt.title('Original image')
# 绘制幅值频谱
imgX = scipy.fftpack.fftshift(scipy.fftpack.fft2(imgL))
# log变换,得到的频谱图对比更明显(仅作为分析观察)
powr2 = np.log(np.abs(imgX))
plt.subplot2grid((2,3),(1,0))
plt.imshow(powr2,cmap=plt.cm.gray)
plt.clim([0,15])
plt.axis('off')
plt.title('Amplitude spectrum')
# 用高斯函数作为过滤核,宽度为0.1
width = .1 # width of gaussian (normalized Z units)
lims = np.shape(imgL)
xr = stats.zscore(np.arange(lims[0]))
[x,y] = np.meshgrid(xr,xr)
# add 1- at beginning of the next line to invert the filter
gaus2d = np.exp( -( x**2 + y**2 ) / (2*width**2) )
# 绘制高斯函数
plt.subplot2grid((2,3),(1,1))
plt.imshow(gaus2d,cmap=plt.cm.gray)
plt.axis('off')
plt.title('Gain function')
# 绘制调制过的幅值频谱
plt.subplot2grid((2,3),(1,2))
plt.imshow( np.log(np.abs( np.multiply(imgX,gaus2d)) ) ,cmap=plt.cm.gray)
plt.axis('off')
plt.clim([0,15])
plt.title('Modulated spectrum')
# 还原成图像
# 注意,调制过后的频谱要进过fftshift处理,把低频移到周边,高频移到中间
imgrecon = np.real(scipy.fftpack.ifft2(scipy.fftpack.fftshift( np.multiply(imgX,gaus2d) ) ) )
plt.subplot2grid((2,2),(0,1))
plt.imshow( imgrecon ,cmap=plt.cm.gray)
plt.axis('off')
plt.title('Filtered image')
plt.show()
# 加载图片图片
lenna = np.asarray( Image.open("Lenna.png") )
# 对RGB通道求均值 axis=2表示RGB通道
imgL = np.mean(lenna,axis=2)
# 绘制原图
plt.subplot2grid((2,2),(0,0))
plt.imshow(imgL,cmap=plt.cm.gray)
# plt.axis('off')
plt.title('Original image')
# 绘制幅值频谱
imgX = scipy.fftpack.fftshift(scipy.fftpack.fft2(imgL))
# log变换,得到的频谱图对比更明显(仅作为分析观察)
powr2 = np.log(np.abs(imgX))
plt.subplot2grid((2,3),(1,0))
plt.imshow(powr2,cmap=plt.cm.gray)
plt.clim([0,15])
plt.axis('off')
plt.title('Amplitude spectrum')
# 用高斯函数作为过滤核,宽度为0.1
width = .1 # width of gaussian (normalized Z units)
lims = np.shape(imgL)
xr = stats.zscore(np.arange(lims[0]))
[x,y] = np.meshgrid(xr,xr)
# add 1- at beginning of the next line to invert the filter
gaus2d = np.exp( -( x**2 + y**2 ) / (2*width**2) )
# 绘制高斯函数
plt.subplot2grid((2,3),(1,1))
plt.imshow(gaus2d,cmap=plt.cm.gray)
plt.axis('off')
plt.title('Gain function')
# 绘制调制过的幅值频谱
plt.subplot2grid((2,3),(1,2))
plt.imshow( np.log(np.abs( np.multiply(imgX,gaus2d)) ) ,cmap=plt.cm.gray)
plt.axis('off')
plt.clim([0,15])
plt.title('Modulated spectrum')
# 还原成图像
# 注意,调制过后的频谱要进过fftshift处理,把低频移到周边,高频移到中间
imgrecon = np.real(scipy.fftpack.ifft2(scipy.fftpack.fftshift( np.multiply(imgX,gaus2d) ) ) )
plt.subplot2grid((2,2),(0,1))
plt.imshow( imgrecon ,cmap=plt.cm.gray)
plt.axis('off')
plt.title('Filtered image')
plt.show()
如果对高斯核取反,可以生成图像的轮廓。这是取反后保留高频信号,去掉低频信号,而高频信号对应的是图像中颜色发生突变的地方

改动一行代码即可:
# add 1- at beginning of the next line to invert the filter
gaus2d = 1 - np.exp( -( x**2 + y**2 ) / (2*width**2) )
拓展知识,你可能见过用高斯函数对一张图片进行模糊,可以理解为将图像与高斯核进行卷积,而时域(空间域)的卷积,等于频域的乘积。且高斯函数比较特殊,它的频域也是高斯函数,所以本质上,你看到的算法和这个案例是一回事。
写在最后
关于傅里叶变换,在有些学校是一门专门的课程,而且有一些前置的课程要求,比如线性代数、微积分、微分方程、复变函数,还需要一点信号处理的知识。
还有很多细节可以深入挖掘,一篇文章里不可能整理出所有的知识。这两篇文章的意义,是让初学者、非相关行业从业者,可以快速的了解傅里叶变换的原理,能看懂信号频谱的意义,能上手简单的图像频域处理。文章来源:https://www.toymoban.com/news/detail-434253.html
后续如果你还想深入理解,你需要系统的学习信号处理的课程。文章来源地址https://www.toymoban.com/news/detail-434253.html
到了这里,关于傅里叶变换及应用python版(2)的文章就介绍完了。如果您还想了解更多内容,请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章,希望大家以后多多支持TOY模板网!