逆透视变换——变换矩阵的Python实现-Toy模板网

这篇具有很好参考价值的文章主要介绍了逆透视变换——变换矩阵的Python实现。希望对大家有所帮助。如果存在错误或未考虑完全的地方，请大家不吝赐教，您也可以点击"举报违法"按钮提交疑问。

Reference

透视变换原理和变换矩阵的python实现
个人理解，可能有误，欢迎讨论。
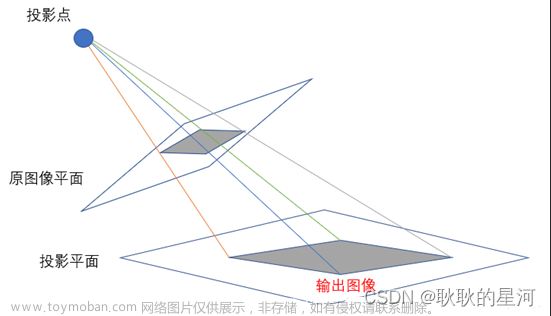
进行透视变换，需要选择四个点，这些点定义了一个长方形，但是在原始图像中由于照相角度等问题，它并没有呈现出是一个长方形，为了变换视角，我们需要进行透视变换。
透视变换本质上是将图片从一种视角通过四个点之间的线性变换得到另一种视角。

计算公式

透视变换矩阵：

逆透视变换——变换矩阵的Python实现
我们定义目标点矩阵为，定义源点矩阵为。
这是从二维像素坐标映射到三维世界坐标，我们这里的主要还是想把像素坐标映射到另一个像素坐标。
采用
对于每一对都满足下列等式

因此，我们可以得到公式（1）
逆透视变换——变换矩阵的Python实现
上下相乘，继续推导可得：

我们需要求得，另为未知数，将方程转换为矩阵 $A X = 0$

此时有9个未知数，我们需要用9个方程来求解，对于一对匹配点我们可以得到两个方程。
为啥我们只需要4对匹配点就能求解上面的方程勒。

8未知数

我们发现对于公式（1）可以写成以下形式，结果不会改变。
逆透视变换——变换矩阵的Python实现其中 $\alpha$ 为不为0的数
此时，将上述公式映射回矩阵形式，我们可以得到
因此，我们可以得到

此时就只有8个未知数了，我们就只需要找4组对应点就可以求解方程。
反应到求解公式上就如下所示。
逆透视变换——变换矩阵的Python实现
最后一位为常数1，我们可以修改公式为 公式（3）文章来源地址https://www.toymoban.com/news/detail-434334.html

代码求解——自己实现

# 此处的src是原坐标数组，dst是目标坐标数组
def WarpPerspectiveMatrix(src, dst):
    assert src.shape[0] == dst.shape[0] and src.shape[0] >= 4

    nums = src.shape[0]
    # 4组对应点，每组2行8列
    # 总共8行8列的数组，对应公式（3）中最左边的矩阵
    A = np.zeros((2 * nums, 8))
    # 4组对应点，每组2行1列
    # 总共8行1列，对应公式（3）中最右边的矩阵
    B = np.zeros((2 * nums, 1))
    # 矩阵赋值，0下标为x值，1下标为y值
    for i in range(0, nums):
        A_i = src[i,:]
        B_i = dst[i,:]
        A[2*i, :] = [A_i[0], A_i[1], 1, 0, 0, 0, -A_i[0]*B_i[0], -A_i[1]*B_i[0]]
        B[2*i] = B_i[0]

        A[2*i+1, :] = [0, 0 , 0, A_i[0], A_i[1], 1, -A_i[0]*B_i[1], -A_i[1]*B_i[1]]
        B[2*i+1] = B_i[1]

	# 转换为矩阵
    A = np.mat(A)
    # 求解未知数值，.I表示求逆
    warpMatrix = A.I * B

	# 矩阵后处理，主要是将a33的1值赋值回去
    warpMatrix = np.array(warpMatrix).T[0]
    warpMatrix = np.insert(warpMatrix, warpMatrix.shape[0], values=1.0, axis=0)
    warpMatrix = warpMatrix.reshape((3, 3))
    return warpMatrix

代码求解——Opencv实现

# 注意，这里的src和dst，本人验证，使用np.float32（）定义可以不出错
M = cv2.getPerspectiveTransform(src, dst)

src = np.float32([[34 * 720 / 160, 113 * 1280 / 288], [34 * 720 / 160, 186 * 1280 / 288], [157 * 720 / 160, 50 * 1280 / 288], [157 * 720 / 160, 244 * 1280 / 288]])
dst = np.float32([[150, 50], [150, 490], [780, 50], [780, 490]])


def WarpPerspectiveMatrix(src, dst):
    assert src.shape[0] == dst.shape[0] and src.shape[0] >= 4

    nums = src.shape[0]
    A = np.zeros((2 * nums, 8))
    B = np.zeros((2 * nums, 1))
    for i in range(0, nums):
        A_i = src[i,:]
        B_i = dst[i,:]
        A[2*i, :] = [A_i[0], A_i[1], 1, 0, 0, 0, -A_i[0]*B_i[0], -A_i[1]*B_i[0]]
        B[2*i] = B_i[0]

        A[2*i+1, :] = [0, 0 , 0, A_i[0], A_i[1], 1, -A_i[0]*B_i[1], -A_i[1]*B_i[1]]
        B[2*i+1] = B_i[1]

    A = np.mat(A)
    warpMatrix = A.I * B

    warpMatrix = np.array(warpMatrix).T[0]
    warpMatrix = np.insert(warpMatrix, warpMatrix.shape[0], values=1.0, axis=0)
    warpMatrix = warpMatrix.reshape((3, 3))
    return warpMatrix

M = WarpPerspectiveMatrix(src, dst)
print(M)
M = cv2.getPerspectiveTransform(src, dst)
print(M)

# 自己实现的
[[ 6.41178433e+00  0.00000000e+00 -7.04158205e+02]
 [ 1.54253726e+00  2.50298025e+00 -1.40077892e+03]
 [ 5.52700641e-03  0.00000000e+00  1.00000000e+00]]
# opencv官方的
[[ 6.41178433e+00  0.00000000e+00 -7.04158205e+02]
 [ 1.54253726e+00  2.50298025e+00 -1.40077892e+03]
 [ 5.52700641e-03 -1.08420217e-19  1.00000000e+00]]