🐶博主主页:@ᰔᩚ. 一怀明月ꦿ
❤️🔥专栏系列:线性代数,C初学者入门训练,题解C,C的使用文章,「初学」C++
🔥座右铭:“不要等到什么都没有了,才下定决心去做”
🚀🚀🚀大家觉不错的话,就恳求大家点点关注,点点小爱心,指点指点🚀🚀🚀
目录
环形链表
环形链表 II
环形链表
给你一个链表的头节点
head,判断链表中是否有环。如果链表中有某个节点,可以通过连续跟踪next指针再次到达,则链表中存在环。 为了表示给定链表中的环,评测系统内部使用整数pos来表示链表尾连接到链表中的位置(索引从 0 开始)。注意:pos不作为参数进行传递 。仅仅是为了标识链表的实际情况。如果链表中存在环 ,则返回
true。 否则,返回false。示例 1:
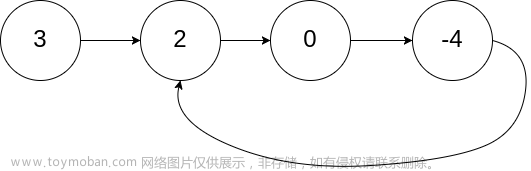
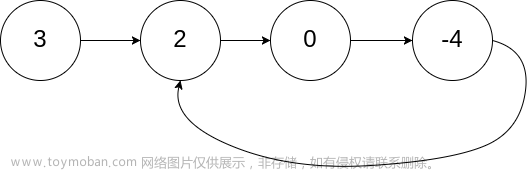
输入:head = [3,2,0,-4], pos = 1 输出:true 解释:链表中有一个环,其尾部连接到第二个节点。示例 2:
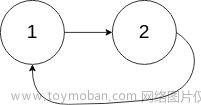
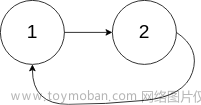
输入:head = [1,2], pos = 0 输出:true 解释:链表中有一个环,其尾部连接到第一个节点。示例 3:
输入:head = [1], pos = -1 输出:false 解释:链表中没有环。提示:
- 链表中节点的数目范围是
[0, 104]-105 <= Node.val <= 105pos为-1或者链表中的一个 有效索引 。进阶:你能用
O(1)(即,常量)内存解决此问题吗?解题思路:
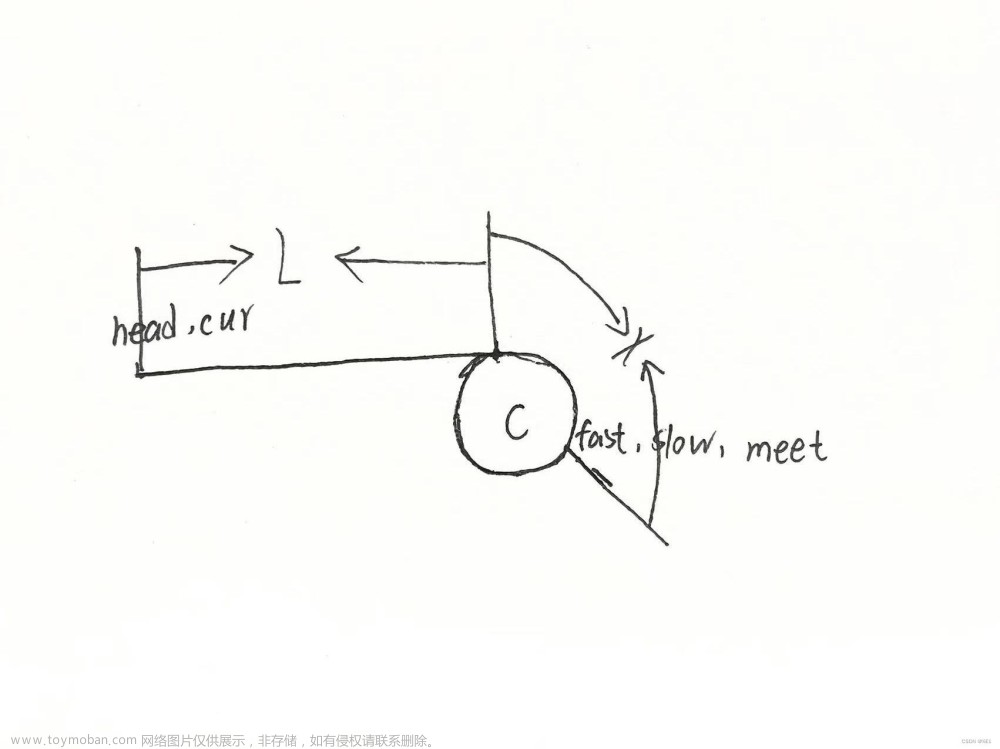
利用双指针的解法,一个慢指针slow,一个快指针fast,slow一次走一步,fast一次走两步,如果fast和slow相遇,说明链表带环,如果fast或fast->next为空,就说明链表不带环。
bool hasCycle(struct ListNode *head) { struct ListNode* slow=head; struct ListNode* fast=head; while(fast&&fast->next) { slow=slow->next; fast=fast->next->next; if(slow==fast) { return true; } } return false; }注意事项:
假设该链表带环
1.slow走一步,fast走两步,slow和fast一定会相遇吗?2.slow走一步,fast走n(3,4,5……)步,slow和fast会相遇吗?
a.slow走一步,fast走两步,slow和fast一定会相遇吗?
结论:slow和fast一定会相遇
证明如下:
fast会先进入环,slow后进入环,假设slow进环时,slow与fast之间的距离是N,slow进环以后,fast开始追击slow,slow每走一步,fast走两步,它们之间的距离缩小1,追击过程中,,它们之间距离的变化:
NN-1
N-2
...
2
1
0
当它们之间的距离为0的时候,说明slow和fast相遇了。即证明slow走一步,fast走两步,slow和fast一定会相遇。
b.slow走一步,fast走n(3,4,5……)步,slow和fast会相遇吗?
假设slow走一步,fast走三步,slow和fast一定会相遇吗?
结论:slow和fast不一定会相遇
fast会先进入环,slow后进入环,假设slow进环时,slow与fast之间的距离是N,slow进环以后,fast开始追击slow,slow每走一步,fast走三步,它们之间的距离缩小2,追击过程中,,它们之间距离的变化:
当N是偶数时
N
N-2
N-4
...
4
2
0
当它们之间的距离为0的时候,说明slow和fast相遇了
当N是奇数时
N
N-2
N-4
...
3
1
-1
当它们之间的距离为-1的时候,说明slow和fast错过了,进入下一轮追击,slow和fast的距离变成了C-1(C是环的长度),如果C-1是偶数则下一轮追上,否则永远追不上。
环形链表 II
给定一个链表的头节点
head,返回链表开始入环的第一个节点。 如果链表无环,则返回null。如果链表中有某个节点,可以通过连续跟踪
next指针再次到达,则链表中存在环。 为了表示给定链表中的环,评测系统内部使用整数pos来表示链表尾连接到链表中的位置(索引从 0 开始)。如果pos是-1,则在该链表中没有环。注意:pos不作为参数进行传递,仅仅是为了标识链表的实际情况。不允许修改 链表。
示例 1:
输入:head = [3,2,0,-4], pos = 1 输出:返回索引为 1 的链表节点 解释:链表中有一个环,其尾部连接到第二个节点。示例 2:
输入:head = [1,2], pos = 0 输出:返回索引为 0 的链表节点 解释:链表中有一个环,其尾部连接到第一个节点。示例 3:
输入:head = [1], pos = -1 输出:返回 null 解释:链表中没有环。提示:
- 链表中节点的数目范围在范围
[0, 104]内-105 <= Node.val <= 105pos的值为-1或者链表中的一个有效索引进阶:你是否可以使用
O(1)空间解决此题?解题思路:
方法一:
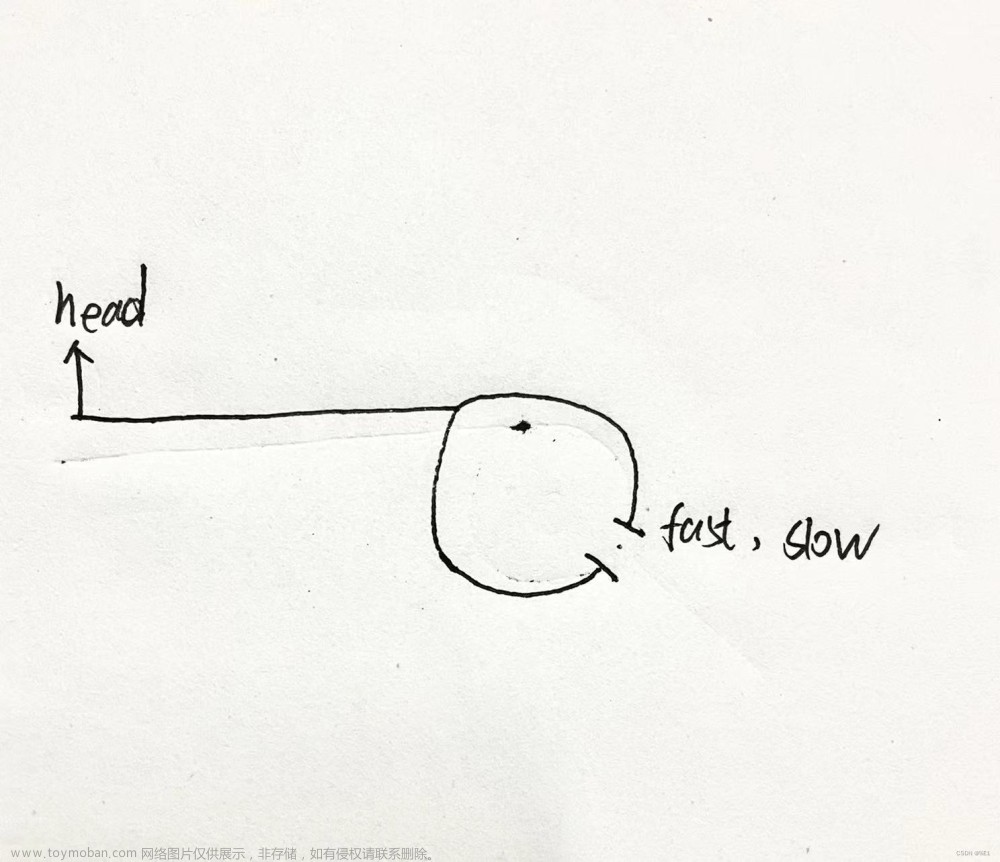
已知结论,一个指针从相遇点出发,另一个指针从链表表头开始走,它们一定会在入口相遇。
struct ListNode *detectCycle(struct ListNode *head) { struct ListNode* fast=head; struct ListNode* slow=head; while(fast&&fast->next) { fast=fast->next->next; slow=slow->next; if(fast==slow)//这里之前都是复用,判断链表是否带环的原码 { struct ListNode* meet=slow;//相遇点的指针 struct ListNode* cur=head;//链表表头指针 while(meet!=cur) { cur=cur->next; meet=meet->next; } return meet;//入口点的位置 } } return NULL; }结论的验证:
前提:slow走一步,fast走两步
推论:fast走的路程是slow的两倍
声明:链表表头到环入口点的距离:L,环入口点到相遇点点距离:X,环的长度:C
slow走的路程:L+X(因为1圈之内,fast必定能够追上slow)
fast走的路程:L+X+n*C(如果L很长,C很短,所以在slow进入环之前,fast可能走了不止一圈了,所以是n*C)
由推论可以的到:2*(L+X)=L+X+n*C L=n*C-X
得到L=n*C-X,即证明了结论了
方法二:
在相遇的时候,将相遇的节点和下一个节点断开,如图所示:
这样我们就可以,帮这个题看成,找两个链表相交的第一个节点。
struct ListNode *detectCycle(struct ListNode *head) { struct ListNode* slow=head; struct ListNode* fast=head; while(fast&&fast->next) { slow=slow->next; fast=fast->next->next; if(slow==fast) { struct ListNode* meet=fast; struct ListNode* meetNext=meet->next; meet->next=NULL; int LenHead=0,LenMeetNext=0; struct ListNode* n1=meetNext; struct ListNode* n2=head; while(n1) { n1=n1->next; LenHead++; } while(n2) { n2=n2->next; LenMeetNext++; } int gap=abs(LenHead-LenMeetNext); struct ListNode* longlist=meetNext; struct ListNode* shortlist=head; if(LenHead<LenMeetNext) { longlist=head; shortlist=meetNext; } while(gap--) { longlist=longlist->next; } while(longlist!=shortlist) { longlist=longlist->next; shortlist=shortlist->next; } return longlist; } } return NULL; }文章来源:https://www.toymoban.com/news/detail-434739.html
🌸🌸🌸如果大家还有不懂或者建议都可以发在评论区,我们共同探讨,共同学习,共同进步。谢谢大家! 🌸🌸🌸 文章来源地址https://www.toymoban.com/news/detail-434739.html
到了这里,关于C语言中链表经典面试题目的文章就介绍完了。如果您还想了解更多内容,请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章,希望大家以后多多支持TOY模板网!