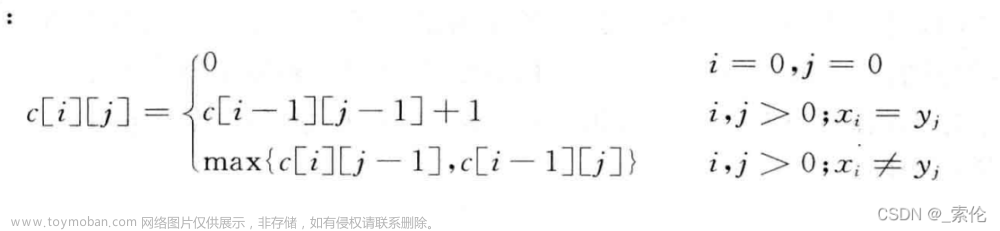算法 DAY52 动态规划10 1143.最长公共子序列 1035.不相交的线 53. 最大子数组和-Toy模板网

这篇具有很好参考价值的文章主要介绍了算法 DAY52 动态规划10 1143.最长公共子序列 1035.不相交的线 53. 最大子数组和。希望对大家有所帮助。如果存在错误或未考虑完全的地方，请大家不吝赐教，您也可以点击"举报违法"按钮提交疑问。

1143.最长公共子序列

本题和动态规划：718. 最长重复子数组 (opens new window)区别在于这里不要求是连续的了

1、dp数组
dp[i][j]：长度为[0, i - 1]的字符串text1与长度为[0, j - 1]的字符串text2的最长公共子序列为dp[i][j]
2、递推公式
因为不强调是连续的，当前dp[i][j] 就有三种路径可以选：dp[i-1][j] dp[i][j-1] dp[i-1][j-1]
当 i != j 时，就延续 i-1 或者延续 j-1。如果 i == j , 那就比 i-1，j-1 多1位。（记不得就去画个图）

 if(text2[j] == text1[i] && j > 0 && i > 0){
		dp[i][j] = dp[i-1][j-1] + 1;
 }
 else if(j > 0 && i > 0){
     dp[i][j] = max(dp[i][j-1],dp[i-1][j]);
 }

3、初始化
要注意，本题的子序列不要求连续，也就是说不只是nums1[i] = nums2[0] 时dp[i][0] = 1，而是 i 后面的都等于1。

class Solution {
public:
    int longestCommonSubsequence(string text1, string text2) {
        vector<vector<int>> dp(text1.size(),vector<int>(text2.size(),0));

        int index1 = text2.find(text1[0]);
        if(index1 >=0 && index1 < text2.size()){
            for(int i = index1; i < text2.size(); ++i){
                dp[0][i] = 1;
            }
        }

        int index2 = text1.find(text2[0]);
        if(index2 >=0 && index2 < text1.size()){
            for(int i = index2; i < text1.size(); ++i){
                dp[i][0] = 1;
            }
        }
        

        for(int i = 0; i < text1.size(); ++i){
            for(int j = 0; j < text2.size();++j){
                if(text2[j] == text1[i] && j > 0 && i > 0){
                    dp[i][j] = dp[i-1][j-1] + 1;
                }
                else if(j > 0 && i > 0){
                    dp[i][j] = max(dp[i][j-1],dp[i-1][j]);
                }
            }
        }
        return dp[text1.size()-1][text2.size()-1];
    }
};

1035.不相交的线

直线不能相交，这就是说明在字符串A中找到一个与字符串B相同的子序列，且这个子序列不能改变相对顺序，只要相对顺序不改变，链接相同数字的直线就不会相交。
本题说是求绘制的最大连线数，其实就是求两个字符串的最长公共子序列的长度！元素位置不改变

class Solution {
public:
    int maxUncrossedLines(vector<int>& nums1, vector<int>& nums2) {
        vector<vector<int>> dp(nums1.size(),vector<int>(nums2.size(),0));
        auto it1 = find(nums2.begin(),nums2.end(),nums1[0]);
        if(it1!=nums2.end()){
            auto index1 = distance(begin(nums2), it1);
            for(int i = index1; i < nums2.size(); ++i){
                dp[0][i] = 1;
            }
        }

        auto it2 = find(nums1.begin(),nums1.end(),nums2[0]);
        if(it2!=nums1.end()){
            auto index2 = distance(begin(nums1), it2);
            for(int i = index2; i < nums1.size(); ++i){
                dp[i][0] = 1;
            }
        }

        for(int i = 0 ; i< nums1.size();++i){
            for(int j = 0; j < nums2.size(); ++j){
                if(nums1[i] == nums2[j] && i>0 &&j>0){
                    dp[i][j] = dp[i-1][j-1] + 1;
                }
                else if(i>0 &&j>0){
                    dp[i][j] = max(dp[i-1][j],dp[i][j-1]);
                }
            }
        }

        return dp[nums1.size()-1][nums2.size()-1];
    }
};

53. 最大子数组和

不难
1、dp[i] : 以nums[i] 结尾的字符串，最大子序列和。
2、递推公式
由于是以nums[i] 结尾，所以dp[i] 的结果一定包含nums[i] ,
dp[i - 1] + nums[i]，即：nums[i]加入当前连续子序列和
nums[i]，即：从头开始计算当前连续子序列和
dp[i] = max(dp[i-1] + nums[i] , nums[i])文章来源地址https://www.toymoban.com/news/detail-435013.html

class Solution {
public:
    int maxSubArray(vector<int>& nums) {
        vector<int> dp(nums.size(),0);
        int res = nums[0];
        dp[0] = nums[0];
        for(int i = 1; i < nums.size();++i){
            dp[i] = max(nums[i],nums[i] + dp[i-1]);
            if(dp[i] > res) res = dp[i];
        }
        return res;
    }
};