[数据结构(C语言版本)上机实验]稀疏矩阵的三元组顺序表压缩存储以及转置实现(含快速转置）-Toy模板网

这篇具有很好参考价值的文章主要介绍了[数据结构(C语言版本)上机实验]稀疏矩阵的三元组顺序表压缩存储以及转置实现(含快速转置）。希望对大家有所帮助。如果存在错误或未考虑完全的地方，请大家不吝赐教，您也可以点击"举报违法"按钮提交疑问。

实现效果：
1、编写程序任意输入一个稀疏矩阵，用三元组顺序表压缩存储稀疏矩阵。
2、对稀疏矩阵进行转置，输出转置后的矩阵。

实验目的

对应《数据结构(C语言版）》第5章数组与广义表实验：

1、掌握下三角矩阵的输入、输出、压缩存储算法；
2、理解稀疏矩阵的三元组表类型定义
3、掌握稀疏矩阵的输入、输出、转置算法。

一、基本概念

o(*￣︶￣*)o请先确保理清一下概念

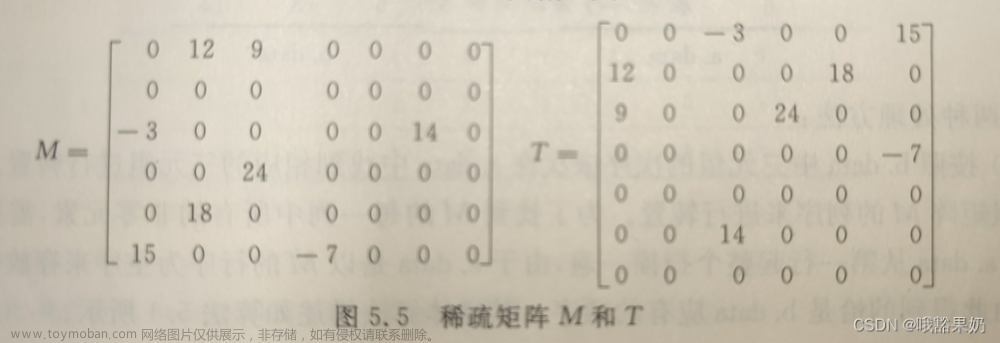
1.稀疏矩阵

假设m*n的矩阵中，有t的非零元，令s=t/m * n,当，s<=0.05时，称此矩阵为稀疏矩阵，简单理解就是非零元特别少的矩阵

//一般矩阵a
    1 2 3
 a= 4 5 6
    7 8 9
    
//稀疏矩阵s
    0 0 0 0 0 
    0 2 0 0 5
 s= 0 0 3 0 0
    0 0 0 0 4

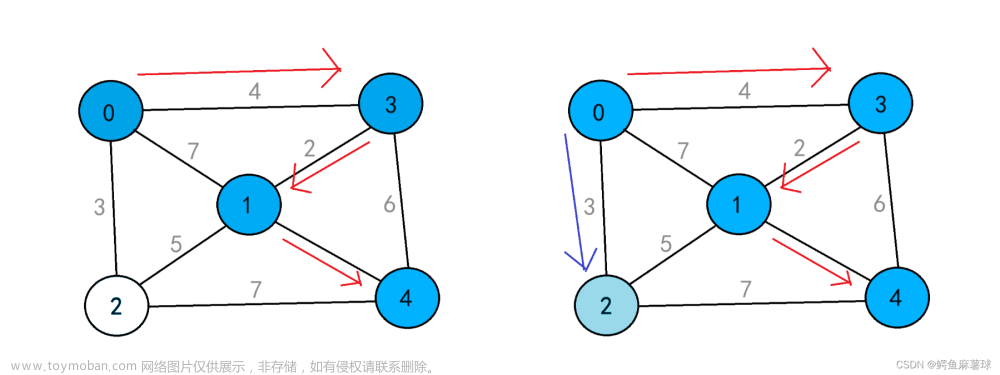
2.矩阵转置

矩阵的转置实际上就是将数据元素的行标和列标互换，即 T(i,j) = M(j,i)
[数据结构(C语言版本)上机实验]稀疏矩阵的三元组顺序表压缩存储以及转置实现(含快速转置）

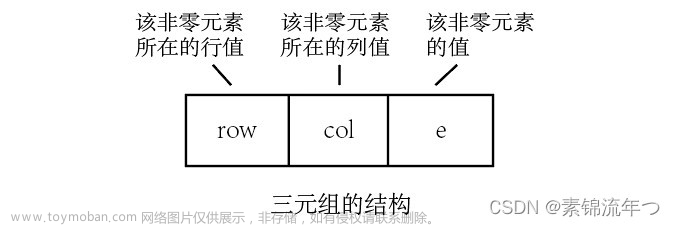
对应三元组的转置
[数据结构(C语言版本)上机实验]稀疏矩阵的三元组顺序表压缩存储以及转置实现(含快速转置）

3.快速转置算法

矩阵的转置过程经历了三个步骤：

矩阵的行数 n 和列数 m 的值交换；
将三元组中的 i 和 j 调换；
转换之后的表同样按照行序（置换前的列序）为主序，进行排序；【两者不同之处】

快速转置算法，预先确定矩阵M中每一列的第一个非零元在转置的三元组中的位置。

时间复杂度由O(nu * tu)提升到O(nu + tu)，尤其是在矩阵的非零元个数tu与mu * nu数量级越接近时差别越明显!

二、完整代码（附详细注释）

提示：本实验环境为VS2019(‾◡◝)

代码如下（示例）：

//Matrix.cpp
//任意输入一个稀疏矩阵，并输出其转置矩阵
#include <stdio.h>
#include <stdlib.h>
#include "SparseMatrix.h"

void TransposeSMatrix(TSMatrix M, TSMatrix& T);
void FastTransposeSMatrix(TSMatrix M, TSMatrix& T);

int main()
{
    TSMatrix M,T;
    //创建稀疏矩阵
    CreateSMartrix(M);
    PrintSMatrix(M);

    printf("1.普通转置\t2.快速转置\t3.退出\n");
    printf("请选择对矩阵的操作：\n");
    int choice = 1;
    while (scanf_s("%d", &choice)) {
        switch (choice) {
        case 1:
            //转置
            TransposeSMatrix(M, T);
            PrintSMatrix(T);
            printf("是否继续操作：");
            break;
        case 2:
            //快速转置
            FastTransposeSMatrix(M, T);
            PrintSMatrix(T);
            printf("是否继续操作：");
            break;
        default:
            printf("程序结束");
            exit(0);          
        }
    }
    return 0;
}

//普通转置，按照三元组在转置矩阵中的存储位置转换
void TransposeSMatrix(TSMatrix M, TSMatrix& T) {
    T.mu = M.mu;//行数
    T.nu = M.nu;//列数
    T.tu = M.tu;//非零元的个数
    if (T.tu) {
        int q = 1;
        for (int col = 1; col <= M.mu; ++col) {
            for (int p = 1; p <= M.nu; ++p) {
                if (M.data[p].j == col) {
                    T.data[q].i = M.data[p].j;
                    T.data[q].j = M.data[p].i;
                    T.data[q].e = M.data[p].e;
                    ++q;
                }
            }
        }
    }
}

//快速转置，按照三元组在原矩阵中的位置转换
//即预先确定M中每一列的第一个元素所在的位置
void FastTransposeSMatrix(TSMatrix M, TSMatrix& T) {
    T.mu = M.mu;//行数
    T.nu = M.nu;//列数
    T.tu = M.tu;//非零元的个数
    int* num = (int*)malloc(M.nu * sizeof(int));//num[col]表示矩阵M中第col列中的非零元素的个数
    int* cpot = (int*)malloc(M.nu * sizeof(int));//cpot[col]指示M中第col列的第一个非零元素在T的位置
    int q, col;
    if (T.tu) {//当矩阵不是零矩阵的时候执行操作
        for (col = 1; col <= M.nu; ++col)
            num[col] = 0;//初始化全部设置为0
        for (int t = 1; t <= M.tu; ++t)
            ++num[M.data[t].j];//按创建三元组的顺序，每列有非零元素时num加一
        cpot[1] = 1;
        for (col = 2; col <= M.nu; ++col)
            cpot[col] = cpot[col - 1] + num[col - 1];
        for (int p = 1; p <= M.tu; ++p) {
            col = M.data[p].j;
            q = cpot[col];
            T.data[q].i = M.data[p].j;
            T.data[q].j = M.data[p].i;
            T.data[q].e = M.data[p].e;
            ++cpot[col];
        }
    }
}

//SparseMatrix.h
#pragma once
#define MAXSIZE 12500 //非零元最大个数

//三元组
typedef struct {
	int i, j;//该元素的行、列
	int e;//该元素的值，此例为整型
}Triple;

//稀疏矩阵
typedef struct {
	Triple data[MAXSIZE + 1];//非零元素三元组，data[0]未用，即矩阵的第一个元素坐标表示为(1,1)
	int mu, nu, tu;//稀疏矩阵的行、列、非零元的个数
}TSMatrix;


//创建稀疏矩阵，采用三元组顺序压缩存储的方式
void CreateSMartrix(TSMatrix& M) {
	printf("请依次输入矩阵的大小:\n行数m\t列数n\t非零元个数t\n");
	int m, n, t;
	scanf_s("%d\t%d\t%d", & m, &n, &t);
	M.mu = m;
	M.nu = n;
	M.tu = t;

	printf("请依次输入矩阵非零元的三元组:\n行坐标i\t列坐标j\t元素值e\n");
	int i, j, e;
	for (int i = 1; i <= t; i++)
	{
		scanf_s("%d\t%d\t%d", &i, &j, &e);
		M.data[i].i = i;
		M.data[i].j = j;
		M.data[i].e = e;
	}
}

//输出稀疏矩阵
void PrintSMatrix(TSMatrix M)
{
	printf("------------------------------\n");
	printf("矩阵的三元组表示：\n");
	printf("i\tj\te\n");
	for (int i = 1; i <= M.tu; i++)
	{
		printf("%d\t%d\t%d\n", M.data[i].i, M.data[i].j, M.data[i].e);
	}
	printf("------------------------------\n");
}