k近邻算法KNN是一种简单而强大的算法,可用于分类和回归任务。他实现简单,主要依赖不同的距离度量来判断向量间的区别,但是有很多距离度量可以使用,所以本文演示了KNN与三种不同距离度量(Euclidean、Minkowski和Manhattan)的使用。

KNN算法概述
KNN是一种惰性、基于实例的算法。它的工作原理是将新样本的特征与数据集中现有样本的特征进行比较。然后算法选择最接近的k个样本,其中k是用户定义的参数。新样本的输出是基于“k”最近样本的多数类(用于分类)或平均值(用于回归)确定的。
有很多距离度量的算法,我们这里选取3个最常用度量的算法来进行演示:
1、欧氏距离 Euclidean Distance
def euclidean_distance(x1, x2):
return math.sqrt(np.sum((x1 - x2)**2))
euclidean_distance函数计算多维空间中两点(x1和x2)之间的欧氏距离,函数的工作原理如下:
- 从x1元素中减去x2,得到对应坐标之间的差值。
- 使用**2运算将差值平方。
- 使用np.sum()对差的平方求和。
- 使用math.sqrt()取总和的平方根。
欧几里得距离是欧几里得空间中两点之间的直线距离。通过计算欧几里得距离,可以识别给定样本的最近邻居,并根据邻居的多数类(用于分类)或平均值(用于回归)进行预测。在处理连续的实值特征时,使用欧几里得距离很有帮助,因为它提供了一种直观的相似性度量。
2、曼哈顿距离 Manhattan Distance
两点坐标的绝对差值之和。
def manhattan_distance(x1, x2):
return np.sum(np.abs(x1 - x2))
Manhattan _distance函数计算多维空间中两点(x1和x2)之间的曼哈顿距离,函数的工作原理如下:
- 用np计算x1和x2对应坐标的绝对差值。Abs (x1 - x2)
- 使用np.sum()对绝对差进行求和。
曼哈顿距离,也称为L1距离或出租车距离,是两点坐标的绝对差值之和。它代表了当运动被限制为网格状结构时,点之间的最短路径,类似于在城市街道上行驶的出租车。
在数据特征具有不同尺度的情况下,或者当问题域的网格状结构使其成为更合适的相似性度量时,使用曼哈顿距离可能会有所帮助。曼哈顿距离可以根据样本的特征来衡量样本之间的相似性或差异性。
与欧几里得距离相比,曼哈顿距离对异常值的敏感性较低,因为它没有对差异进行平方。这可以使它更适合于某些数据集或异常值的存在可能对模型的性能产生重大影响的问题。
3、闵可夫斯基距离 Minkowski Distance
它是欧几里得距离和曼哈顿距离的一般化的表现形式,使用p进行参数化。当p=2时,它变成欧氏距离,当p=1时,它变成曼哈顿距离。
def minkowski_distance(x1, x2, p):
return np.power(np.sum(np.power(np.abs(x1 - x2), p)), 1/p)
minkowski_distance函数计算多维空间中两点(x1和x2)之间的闵可夫斯基距离。
当你想要控制单个特征的差异对整体距离的影响时,使用闵可夫斯基距离会很有帮助。通过改变p值,可以调整距离度量对特征值或大或小差异的灵敏度,使其更适合特定的问题域或数据集。
闵可夫斯基距离可以根据样本的特征来衡量样本之间的相似性或不相似性。该算法通过计算适当p值的闵可夫斯基距离,识别出给定样本的最近邻居,并根据邻居的多数类(用于分类)或平均值(用于回归)进行预测。
KNN 算法的代码实现
因为KNN算法的原理很简单,所以我们这里直接使用Python实现,这样也可以对算法有一个更好的理解:
defknn_euclidean_distance(X_train, y_train, X_test, k):
# List to store the predicted labels for the test set
y_pred= []
# Iterate over each point in the test set
foriinrange(len(X_test)):
distances= []
# Iterate over each point in the training set
forjinrange(len(X_train)):
# Calculate the distance between the two points using the Euclidean distance metric
dist=euclidean_distance(X_test[i], X_train[j])
distances.append((dist, y_train[j]))
# Sort the distances list by distance (ascending order)
distances.sort()
# Get the k nearest neighbors
neighbors=distances[:k]
# Count the votes for each class
counts= {}
forneighborinneighbors:
label=neighbor[1]
iflabelincounts:
counts[label] +=1
else:
counts[label] =1
# Get the class with the most votes
max_count=max(counts, key=counts.get)
y_pred.append(max_count)
returny_pred
这个’ knn_euclidean_distance ‘函数对于解决分类问题很有用,因为它可以根据’ k '个最近邻居中的大多数类进行预测。该函数使用欧几里得距离作为相似性度量,可以识别测试集中每个数据点的最近邻居,并相应地预测它们的标签。我们实现的代码提供了一种显式的方法来计算距离、选择邻居,并根据邻居的投票做出预测。
在使用曼哈顿距离时,KNN算法与欧氏距离保持一致,只需要将距离计算函数euclidean_distance修改为manhattan_distance。而闵可夫斯基距离则需要多加一个参数p,实现代码如下:
defknn_minkowski_distance(X_train, y_train, X_test, k, p):
# List to store the predicted labels for the test set
y_pred= []
# Iterate over each point in the test set
foriinrange(len(X_test)):
distances= []
# Iterate over each point in the training set
forjinrange(len(X_train)):
# Calculate the distance between the two points using the Minkowski distance metric
dist=minkowski_distance(X_test[i], X_train[j], p)
distances.append((dist, y_train[j]))
# Sort the distances list by distance (ascending order)
distances.sort()
# Get the k nearest neighbors
neighbors=distances[:k]
# Count the votes for each class
counts= {}
forneighborinneighbors:
label=neighbor[1]
iflabelincounts:
counts[label] +=1
else:
counts[label] =1
# Get the class with the most votes
max_count=max(counts, key=counts.get)
y_pred.append(max_count)
returny_pred
距离度量对比
我使用的数据集是乳腺癌数据集,可以在kaggle上直接下载
这个数据集是机器学习和数据挖掘中广泛使用的基准数据集,用于二元分类任务。它是由威廉·h·沃尔伯格(William H. Wolberg)博士及其合作者在20世纪90年代从麦迪逊的威斯康星大学医院收集的。该数据集可通过UCI机器学习存储库公开获取。
Breast Cancer Wisconsin数据集包含569个实例,每个实例有32个属性。这些属性是:
ID number:每个样本的唯一标识符。
Diagnosis:目标变量有两个可能的值——“M”(恶性)和“B”(良性)。
剩下的是30个从乳腺肿块的细针抽吸(FNA)的数字化图像中计算出来的特征。它们描述了图像中细胞核的特征。对每个细胞核计算每个特征,然后求平均值,得到10个实值特征:
- Radius:从中心到周边点的平均距离。
- Texture:灰度值的标准偏差。
- Perimeter:细胞核的周长。
- Area:细胞核的面积。
- Smoothness:半径长度的局部变化。
- Compactness:周长²/面积- 1.0。
- Concavity:轮廓中凹部分的严重程度。
- Concave points:轮廓的凹部分的数目。
- Symmetry:细胞核的对称性。
- Fractal dimension:“Coastline approximation”- 1
对每张图像计算这十个特征的平均值、标准误差和最小或最大值(三个最大值的平均值),总共得到30个特征。数据集不包含任何缺失的属性值。
由于数据集包含30个特征,我们需要对数据集进行特征选择。这种方法的主要目的是通过选择与目标变量具有强线性关系的较小的特征子集来降低数据集的维数。通过选择高相关性的特征,目的是保持模型的预测能力,同时减少使用的特征数量,潜在地提高模型的性能和可解释性。这里需要注意的是,该方法只考虑特征与目标变量之间的线性关系,如果底层关系是非线性的,或者特征之间存在重要的交互作用,则该方法可能无效。
读取数据并计算相关系数:
df=pd.read_csv('/kaggle/input/breast-cancer-wisconsin-data/data.csv')
corr=df.corr()
corr_threshold=0.6
selected_features=corr.index[np.abs(corr['diagnosis']) >=corr_threshold]
new_cancer_data=df[selected_features]
训练代码:
X_train_np=np.array(X_train)
X_test_np=np.array(X_test)
# Convert y_train and y_test to numpy arrays
y_train_np=np.array(y_train)
y_test_np=np.array(y_test)
k_values=list(range(1, 15))
accuracies= []
forkink_values:
y_pred=knn_euclidean_distance(X_train_np, y_train_np, X_test_np, k)
accuracy=accuracy_score(y_test_np, y_pred)
accuracies.append(accuracy)
# Create a data frame to store k values and accuracies
results_df=pd.DataFrame({'k': k_values, 'Accuracy': accuracies})
# Create the interactive plot using Plotly
fig=px.line(results_df, x='k', y='Accuracy', title='KNN Accuracy for Different k Values', labels={'k': 'k', 'Accuracy': 'Accuracy'})
fig.show()
# Get the best k value
best_k=k_values[accuracies.index(max(accuracies))]
best_accuracy=max(accuracies)
print("Best k value is:", best_k , "where accuracy is:" ,best_accuracy)
上面代码使用欧几里得距离将KNN算法应用于分类问题,同时改变邻居的数量(k)以找到最高精度的最佳k值。它使用训练集(X_train_np和y_train_np)来训练模型,使用测试集(X_test_np和y_test_np)来进行预测和评估模型的性能。
k是KNN算法的一个超参数,选择正确的k值对于实现最佳模型性能至关重要,因为k值太小可能导致过拟合,而k值太大可能导致欠拟合。通过可视化k值与其对应的精度之间的关系,可以深入了解模型的性能,并为问题选择最合适的k值。
闵可夫斯基距离的代码修改如下:
# Run the KNN algorithm on the test set for different k and p values
k_values=list(range(1, 15))
p_values=list(range(1, 6))
results= []
forkink_values:
forpinp_values:
y_pred=knn_minkowski_distance(X_train_np, y_train_np, X_test_np, k, p)
accuracy=accuracy_score(y_test_np, y_pred)
results.append((k, p, accuracy))
# Create a data frame to store k, p values, and accuracies
results_df=pd.DataFrame(results, columns=['k', 'p', 'Accuracy'])
# Create the 3D plot using Plotly
fig=go.Figure(data=[go.Scatter3d(
x=results_df['k'],
y=results_df['p'],
z=results_df['Accuracy'],
mode='markers',
marker=dict(
size=4,
color=results_df['Accuracy'],
colorscale='Viridis',
showscale=True,
opacity=0.8
),
text=[f"k={k}, p={p}, Acc={acc:.2f}"fork, p, accinresults]
)])
fig.update_layout(scene=dict(
xaxis_title='k',
yaxis_title='p',
zaxis_title='Accuracy'
))
fig.show()
为了进一步改善我们的结果,我们还可以数据集进行缩放。应用特征缩放的主要目的是确保所有特征具有相同的尺度,这有助于提高基于距离的算法(如KNN)的性能。在KNN算法中,数据点之间的距离对确定它们的相似度起着至关重要的作用。如果特征具有不同的尺度,则算法可能会更加重视尺度较大的特征,从而导致次优预测。通过将特征缩放到均值和单位方差为零,算法可以平等地对待所有特征,从而获得更好的模型性能。
本文将使用StandardScaler()和MinMaxScaler()来扩展我们的数据集。StandardScaler和MinMaxScaler是机器学习中两种流行的特征缩放技术。这两种技术都用于将特征转换为公共尺度,这有助于提高许多机器学习算法的性能,特别是那些依赖于距离的算法,如KNN或支持向量机(SVM)。
使用不同的尺度和不同的距离函数训练KNN,可以进行比较并选择最适合数据集的技术。我们得到了以下结果:

可以使用柱状图表示来更好地分析和理解这些结果。

总结
根据上面的结果,我们可以得到以下的结论:
在不进行特征缩放时,欧几里得距离和闵可夫斯基距离都达到了0.982456的最高精度。
曼哈顿离在所有情况下的精度都比较低,这表明欧几里得或闵可夫斯基距离可能更适合这个问题。当闵可夫斯基距离度量中的p值为2时,它等于欧几里得距离。在我们这个实验中这两个指标的结果是相同的,也证明了这是正确的。
对于欧几里得和闵可夫斯基距离度量,不应用任何特征缩放就可以获得最高的精度。而对于曼哈顿距离,与非缩放数据相比,StandardScaler和MinMaxScaler都提高了模型的性能。这表明特征缩放的影响取决于所使用的距离度量。
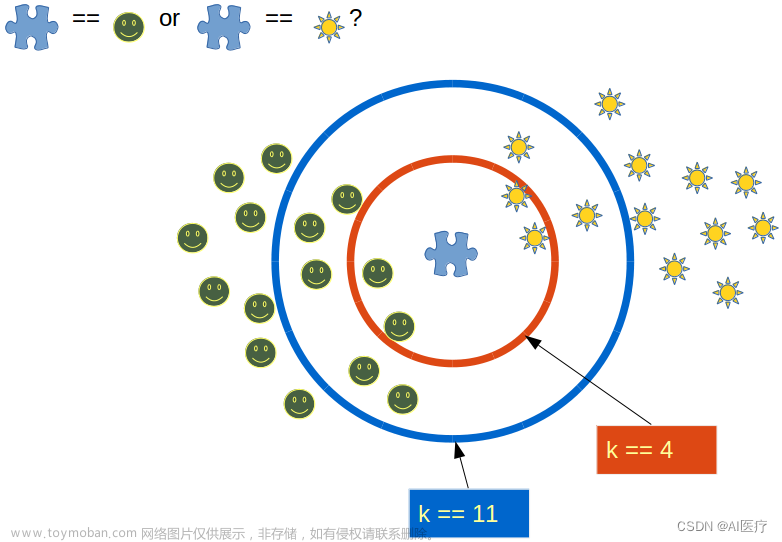
最佳k值:最佳k值取决于距离度量和特征缩放技术。例如,k=11是不应用缩放并且使用欧几里得距离或闵可夫斯基距离时的最佳值,而k=9是使用曼哈顿距离时的最佳值。当应用特征缩放时,最佳k值通常较低,范围在3到11之间。
最后,该问题的最佳KNN模型使用欧式距离度量,无需任何特征缩放,在k=11个邻居时达到0.982456的精度。这应该是我们这个数据集在使用KNN时的最佳解。
如果你想自己实验,完整代码和数据都可以在这里找到:
https://avoid.overfit.cn/post/19200b7f741f4686a9b6ada15552d1ba文章来源:https://www.toymoban.com/news/detail-435147.html
作者:Abdullah Siddique文章来源地址https://www.toymoban.com/news/detail-435147.html
到了这里,关于KNN中不同距离度量对比和介绍的文章就介绍完了。如果您还想了解更多内容,请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章,希望大家以后多多支持TOY模板网!