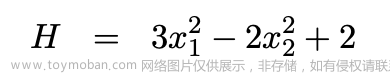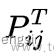量子退火Python实战（3）：投资组合优化（Portfolio） MathorCup2023特供PyQUBO教程-Toy模板网

这篇具有很好参考价值的文章主要介绍了量子退火Python实战（3）：投资组合优化（Portfolio） MathorCup2023特供PyQUBO教程。希望对大家有所帮助。如果存在错误或未考虑完全的地方，请大家不吝赐教，您也可以点击"举报违法"按钮提交疑问。

前言

提示：包含pyQUBO用法：

最近MathorCup2023的A题刚好是投资组合的QUBO建模，刚好有篇日文文章是讲这个的，直接翻译过来。供大家参考。【因为还没有获得作者同意，暂且没有把文章设置为翻译，之后会设置成翻译，或者再加一下自己的东西变成原创。】

《量子アニーリングを用いたポートフォリオ最適化 – 量子アニーリングソリューションコンテスト》
https://qard.is.tohoku.ac.jp/T-Wave/?p=1987

一、什么是投资组合优化？

什么是投资组合优化？

投资组合优化是在考虑风险和收益的情况下寻找资产（投资组合）的最佳组合。投资组合优化有多种理论，但这次我们基于现代投资组合理论进行投资组合优化。

什么是现代投资组合理论？

这是对现代投资组合理论（又名现代投资理论）的描述。

它基于美国哈里·马科维茨于 1950 年代建立的多元化投资理论。为了在资产管理中期望一定的回报同时抑制价格波动风险，将大量股票和多种资产分散投资为一个投资组合是有效的。除了价格波动风险及其包含率外，它由表示任何两个问题之间价格变动的连贯性的相关系数决定。他因在投资理论方面的开创性工作而获得 1990 年诺贝尔经济学奖。

然而，该理论建立在不切实际的假设之上，例如假设股票的价格波动风险从过去到未来都不会发生变化。为此，2008年雷曼震荡后，众多金融资产之间的相关系数增加，同时价格波动的风险也增加，也有人指出该理论的局限性，认为有局限性。

二、投资组合优化建模

1. 目标函数：回报

最大化回报和最小化风险（协方差）被视为最佳投资组合措施。
代表收益回报的目标函数如下：

量子退火Python实战（3）：投资组合优化（Portfolio） MathorCup2023特供PyQUBO教程

2.约束函数：风险

量子退火Python实战（3）：投资组合优化（Portfolio） MathorCup2023特供PyQUBO教程

3.最终优化目标函数

上面两个函数相加就是最终优化的目标函数。
量子退火Python实战（3）：投资组合优化（Portfolio） MathorCup2023特供PyQUBO教程
系数A应根据重点是最大化回报还是最小化风险来调整。

三、基于PyQUBO实现

1. 获取数据

首先，使用pandas_datareader 从yahoo finance 获取股价数据。
这一次，我们将使用具有代表性的美国股票指数 DOW30 指数中包含的 30 只股票的 2018 年数据来优化投资组合。

import pandas_datareader.data as web
import datetime

start = datetime.datetime(2018, 1, 2)
end = datetime.datetime(2018, 12, 31)
DOW30 = ['AAPL','AMGN','AXP','BA','CAT','CRM','CSCO','CVX','DIS','GS','HD','HON', 'IBM','INTC','JNJ','JPM','KO','MCD','MMM','MRK','MSFT','NKE', 'PG','TRV','UNH','V','VZ','WBA','WMT']
stockcodes = DOW30+DOW30

data = web.DataReader(DOW30, 'yahoo', start, end)
df_price_DOW30 = data['Adj Close']

2. 数据处理

从前面得到的股价数据中，求出每只股票每天的几何平均收益和协方差矩阵。

补充（什么是几何平均数？）

import numpy as np
import matplotlib.pyplot as plt
from scipy.stats.mstats import gmean 

df_price0 = pd.merge(df_price, df_price, on='Date')
rates = []

for sc in stockcodes:
    df = df_price.loc[:,sc]
    return_rate = np.zeros(len(df.values))
    for k in range(len(df.values)-1):
        return_rate[k+1] = (df[k+1] - df[k])/df[k]
  
    rates.append(return_rate)

N = len(stockcodes)

list_price_start = np.zeros(N)
for n in range(N):
    list_price_start[n] = df_price.loc['2018-01-02',stockcodes][n]
    
list_price_end = np.zeros(N)
for n in range(N):
    list_price_end[n] = df_price.loc['2018-12-31',stockcodes][n]

#求几何平均w1
for k in range(N):
    for n in range(len(rates[1])):
                   rates[k][n] = rates[k][n]+1

w_1 = np.zeros(N)
for k in range(N):
    w_1[k] = gmean(rates[k])

w = np.zeros(N)
for n in range(N):
    w[n] = w_1[n]-1

for k in range(N):
    for n in range(len(rates[1])):
                   rates[k][n] = rates[k][n]-1

3. 目标函数PyQUBO实现

根据之前获得的每只股票的每日几何平均收益和协方差矩阵，准备使用 PyQUBO 进行优化的目标函数。


from pyqubo import Array, Constraint, Placeholder, solve_qubo

x = Array.create('x', shape=N, vartype='BINARY')# 二值变量

K = 1000 #投资额
constr = (((np.dot(x,list_price_start))-0.9*K)/10)**2 #预算约束

#回报部分的目标函数
cost = 0
for i in range(N):
    cost = cost - w[i]*x[i]
#风险部分的约束函数
cost2 = 0
for i in range(N):
    for j in range(N):
        cost2 = cost2 +x[i]*x[j]*np.sum((rates[i]-w[i])*(rates[j]-w[j]))/len(rates[i])
#整体的目标函数
cost_func = 2*cost + cost2 + Placeholder('a')*Constraint(constr, label='Kconstr') 
model = cost_func.compile()
max_coeff = np.max(abs(w))

#调整约束强度
feed_dict = {'a': 17.0*max_coeff}
qubo, offset = model.to_qubo(feed_dict=feed_dict)

4. OpenJij实施优化

这一次，我们将使用 SQA（模拟量子退火）库 OpenJij 来执行优化。

from openjij import SQASampler
sampler = SQASampler(num_sweeps=3000)
R = 300
sampleset = sampler.sample_qubo(qubo,num_reads=R)
print(sampleset.record)