【数据结构】栈与队列经典oj题-Toy模板网

这篇具有很好参考价值的文章主要介绍了【数据结构】栈与队列经典oj题。希望对大家有所帮助。如果存在错误或未考虑完全的地方，请大家不吝赐教，您也可以点击"举报违法"按钮提交疑问。

【数据结构】栈与队列经典oj题

🚀write in front🚀
📜所属专栏：初阶数据结构
🛰️博客主页：睿睿的博客主页
🛰️代码仓库：🎉VS2022_C语言仓库
🎡您的点赞、关注、收藏、评论，是对我最大的激励和支持！！！
关注我，关注我，关注我，你们将会看到更多的优质内容！！

【数据结构】栈与队列经典oj题

前言

例题1：循环队列

栈两种线性表示都能实现，队列呢？队列适合使用链表实现，使用顺序结构(即固定的连续空间)实现时会出现假溢出的问题，因此大佬们设计出了循环队列，循环队列就是为了解决顺序结构实现队列假溢出问题的现在我们来看看用顺序表实现队列：

【数据结构】栈与队列经典oj题
因为队列长度有限，所以我们要及时的判断什么时候队列满了。那么怎么判断队列是否满了呢？
如果我们通过队尾和队顶是否相等来判断是否填满就会发现，在队列空的时候，队尾也等于对队顶。所以我们不能通过这种方法来判断：
【数据结构】栈与队列经典oj题

那么我们该如何解决呢？
方法1：

加一个size来计数

方法2：
多添加一个位置：

空的情况：
【数据结构】栈与队列经典oj题
满的情况：

下面我们就以方法2来实现代码：

typedef struct 
{
    int *a;
    int front;
    int rear;
    int k;
} MyCircularQueue;

MyCircularQueue* myCircularQueueCreate(int k) 
{
    MyCircularQueue* obj=(MyCircularQueue*)malloc(sizeof(MyCircularQueue));

    obj->a=(int*)malloc(sizeof(int)*(k+1));
    obj->k=k;
    obj->front=obj->rear=0;
    return obj;
}

bool myCircularQueueIsEmpty(MyCircularQueue* obj) 
{
    return obj->rear==obj->front;
}

bool myCircularQueueIsFull(MyCircularQueue* obj) 
{
    return (obj->rear+1)%(obj->k+1)==obj->front;
}
//入队
bool myCircularQueueEnQueue(MyCircularQueue* obj, int value) 
{
    if(myCircularQueueIsFull(obj))
        return false;
        obj->a[obj->rear++]=value;
        obj->rear%=(obj->k+1);
        return true;
}
//出队
bool myCircularQueueDeQueue(MyCircularQueue* obj) 
{
    if(myCircularQueueIsEmpty(obj))
        return false;
        ++obj->front;
        obj->front%=(obj->k+1);
        return true;

}

int myCircularQueueFront(MyCircularQueue* obj) 
{
    if(myCircularQueueIsEmpty(obj))
        return -1;
    
        return obj->a[obj->front];
}

int myCircularQueueRear(MyCircularQueue* obj) 
{
    if(myCircularQueueIsEmpty(obj))
        return -1;

        return obj->a[(obj->rear-1+obj->k+1)%(obj->k+1)];
}

void myCircularQueueFree(MyCircularQueue* obj) 
{
    free(obj->a);
    free(obj);
}

这里我们只要关注这几点，其他的都很好实现：

空的情况：
【数据结构】栈与队列经典oj题
满的情况：

在这里我们学到了如何在数组里建立循环！那就是通过mod数组的长度，就可以使数组循环起来！

找队尾：
【数据结构】栈与队列经典oj题
尾部其实就是rear的后面一个元素，即rear-1，但是当rear等于0的时候，-1就会导致越界。对一个正数加a模a，得到的值不变。对于rear=0的时候进行这个操作就会避免越界的情况。

例题2：用队列实现栈

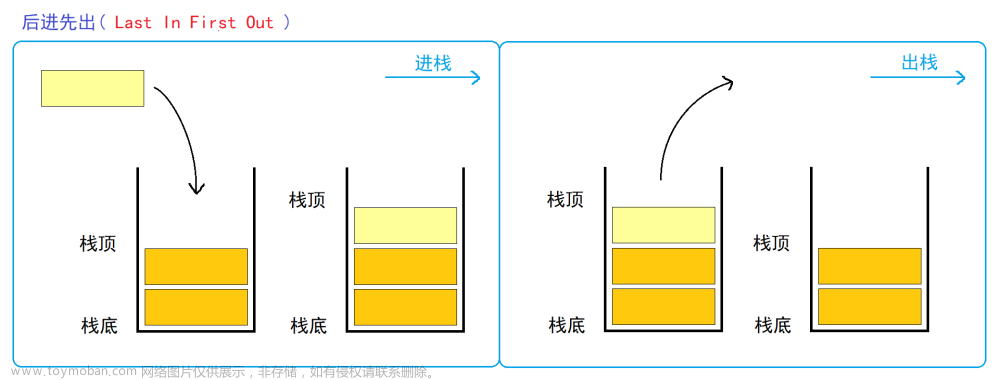
【数据结构】栈与队列经典oj题
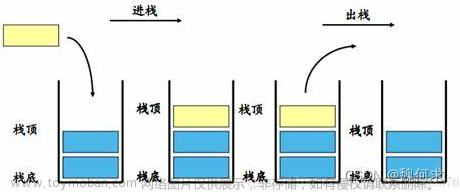
要通过队列表示栈就要熟知他们两个各自的性质。栈是有“先进后出”的特点，队列有“先进先出的特点”，综合她两的特点，我们通过以下方法来实现数据的出入：

保持一个队列为空，一个队列存数据
出栈的时候把前面的数据导入空队列，将最后一个数据pop出去。

具体实现：（队列的代码之前写过，就不展示了，详细：栈与队列）


void QueueInit(Queue* pq);
void QueueDestroy(Queue* pq);
void QueuePush(Queue* pq, QDatatype x);
void QueuePop(Queue* pq);
int QueueSize(Queue* pq);
bool QueueEmpty(Queue* pq);
QDatatype QueueFront(Queue* pq);
QDatatype QueueBack(Queue* pq);

typedef int QDatatype;

typedef struct QueueNode
{
	struct QueueNode* next;
	QDatatype data;
}QNode;

typedef struct Queue
{
	QNode* head;
	QNode* tail;
	int size;
}Queue;


typedef struct 
{
    Queue q1;
    Queue q2;
} MyStack;


MyStack* myStackCreate() 
{
    MyStack*ptr=(MyStack*)malloc(sizeof(MyStack));
    if(ptr==NULL)
    {
        perror("malloc::fail");
        return 0;
    }
    QueueInit(&ptr->q1);
    QueueInit(&ptr->q2);

    return ptr;
}

void myStackPush(MyStack* obj, int x) 
{
    if(!QueueEmpty(&obj->q1))
    {
        QueuePush(&obj->q1,x);
    }
    else
    {
        QueuePush(&obj->q2,x);
    }
}

int myStackPop(MyStack* obj) 
{
    Queue*emptyQ=&obj->q1;
    Queue *noneQ=&obj->q2;
    if(!QueueEmpty(emptyQ))
    {
        emptyQ=&obj->q2;
        noneQ=&obj->q1;
    }
    while(QueueSize(noneQ)>1)
    {
        QueuePush(emptyQ,QueueFront(noneQ));
        QueuePop(noneQ);
    }
    int top=QueueBack(noneQ);
    QueuePop(noneQ);

    return top;
}

int myStackTop(MyStack* obj) 
{
    if(!QueueEmpty(&obj->q1))
    {
        return QueueBack(&obj->q1);
    }
    return QueueBack(&obj->q2);
}

bool myStackEmpty(MyStack* obj) 
{
    return QueueEmpty(&obj->q1)&&QueueEmpty(&obj->q2);
}

void myStackFree(MyStack* obj) {
    QueueDestroy(&obj->q1);
    QueueDestroy(&obj->q2);
    free(obj);
}

例题3：用栈实现队列

【数据结构】栈与队列经典oj题

将一个栈当作输入栈，用于压入 push传入的数据；另一个栈当作输出栈，用于 pop 和peek 操作。

每次 pop 或 peek时，若输出栈为空则将输入栈的全部数据依次弹出并压入输出栈，这样输出栈从栈顶往栈底的顺序就是队列从队首往队尾的顺序。

【数据结构】栈与队列经典oj题
具体代码实现：

typedef int STDataType;
typedef struct Stack
{
	STDataType* a;
	int top; // 栈顶
	int capacity; // 容量
}Stack;
// 初始化栈
void StackInit(Stack* ps);
// 入栈
void StackPush(Stack* ps, STDataType data);
// 出栈
void StackPop(Stack* ps);
// 获取栈顶元素
STDataType StackTop(Stack* ps);
// 获取栈中有效元素个数
int StackSize(Stack* ps);
// 检测栈是否为空，如果为空返回非零结果，如果不为空返回0 
bool empty(Stack* ps);
// 销毁栈
void StackDestroy(Stack* ps);
typedef struct 
{
    Stack pushST;
    Stack popST;
} MyQueue;

int myQueuePeek(MyQueue* obj) ;
MyQueue* myQueueCreate() 
{
    MyQueue*obj=(MyQueue*)malloc(sizeof(MyQueue));
    if(obj==NULL)
    {
        perror("malloc::fail");
        return 0;
    }
    StackInit(&obj->pushST);
    StackInit(&obj->popST);

    return obj;
}

void myQueuePush(MyQueue* obj, int x) 
{
    assert(obj);
    StackPush(&obj->pushST,x);
}

int myQueuePop(MyQueue* obj) 
{
   int top=myQueuePeek(obj);
   StackPop(&obj->popST);
   return top;
}

int myQueuePeek(MyQueue* obj) 
{
    if(empty(&obj->popST))
    {
        while(!empty(&obj->pushST))
        {
            StackPush(&obj->popST,StackTop(&obj->pushST));
            StackPop(&obj->pushST);
        }
    }
    return StackTop(&obj->popST);
}

bool myQueueEmpty(MyQueue* obj) 
{
    return empty(&obj->pushST)&&empty(&obj->popST);
}

void myQueueFree(MyQueue* obj) {
    StackDestroy(&obj->pushST);
    StackDestroy(&obj->popST);

    free(obj);
}