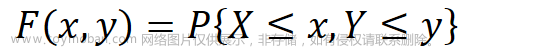条件概率密度函数
题型如下：
- 已知概率密度，求条件概率密度
- 已知x怎么样的情况下y服从的概率（或y怎么样的情况下x服从的概率），求f(x,y)
步骤：对于后两个，是在哪个字母的条件下，哪个字母就在后面。
即，如果是在x=？？？的条件下，那么就选图中第三条方法。
其中：
- 1、2条符合条件概率
- 3、4条是1、2条的变形：把分母乘去等号另一边
- 为什么1、2条中求f(x|y)，则要推出x的范围？因为y是已知条件，它的概率是1。我们要求x，所以也要推x的范围。
接下来看这三道例题，练习套公式：
例1：
解：
这道例题中要先求f(y)，这是二维连续型求边缘概率密度的内容，详情可以看这里二维连续型求边缘密度函数。
x的范围要用y来代入表达
例2：
解：
这里是已知x的条件，所以要用：
这里的“在X=x…的条件下，随机变量y服从f=…”，这里的f其实就是条件概率f(y|x)。
文章来源：https://www.toymoban.com/news/detail-435882.html
求两个随机变量形成的函数的分布
猴博士说，这节课很难，算是概率论里最难的题，考试不一定考的到，可以跳过。文章来源地址https://www.toymoban.com/news/detail-435882.html
到了这里，关于【概率论与数理统计】猴博士 笔记 p24-25 条件概率密度函数、求两个随机变量形成的函数的分布的文章就介绍完了。如果您还想了解更多内容，请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章，希望大家以后多多支持TOY模板网！
