图论--最近公共祖先LCA-Toy模板网

这篇具有很好参考价值的文章主要介绍了图论--最近公共祖先LCA。希望对大家有所帮助。如果存在错误或未考虑完全的地方，请大家不吝赐教，您也可以点击"举报违法"按钮提交疑问。

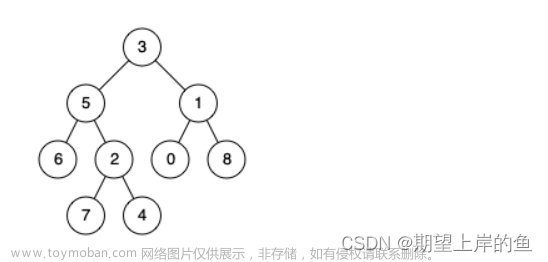
最近公共祖先LCA

LCA（Least Common Ancestors），即最近公共祖先，是指这样一个问题：在有根树中，找出某两个结点u和v最近的公共祖先（另一种说法，离树根最远的公共祖先）
图论--最近公共祖先LCA

最近公共祖先是相对于两个节点来说的，一般来说，最近公共祖先为节点 u和节点 v的最近的公共祖先。若 u 为 v 的祖先或者 v 为 u 的祖先，则LCA(u,v) 就是作为祖先的那个节点。示例图中 86 和 67的 LCA 是 75 ，61和 85的 LCA也是 75 。

以下三种方法，后两种方法比较重要，需要熟记，再求后面次小生成树有很大帮助。

LCA转RMQ

RMQ（Range Minimum/Maximum Query），即区间最值查询，是指这样一个问题：对于长度为n的数列A，回答若干询问RMQ（A,i,j）(i,j<=n)，返回数列A中下标在i，j之间的最小/大值。这两个问题是在实际应用中经常遇到的问题，本文介绍了当前解决这两种问题的比较高效的算法。

RMQ算法

对于该问题，最容易想到的解决方案是遍历，复杂度是O(n)。但当数据量非常大且查询很频繁时，该算法也许会存在问题。

介绍了一种比较高效的在线算法（ST算法）解决这个问题。所谓在线算法，是指用户每输入一个查询便马上处理一个查询。该算法一般用较长的时间做预处理，待信息充足以后便可以用较少的时间回答每个查询。ST（Sparse Table）算法是一个非常有名的在线处理RMQ问题的算法，它可以在O(nlogn)时间内进行预处理，然后在O(1)时间内回答每个查询。

首先是预处理，用动态规划（DP）解决。设A[i]是要求区间最值的数列，F[i, j]表示从第i个数起连续2^j个数中的最大值。例如数列3 2 4 5 6 8 1 2 9 7，F[1，0]表示第1个数起，长度为2^0=1的最大值，其实就是3这个数。 F[1，2]=5，F[1，3]=8，F[2，0]=2，F[2，1]=4……从这里可以看出F[i,0]其实就等于A[i]。这样，DP的状态、初值都已经有了，剩下的就是状态转移方程。我们把F[i，j]平均分成两段（因为f[i，j]一定是偶数个数字），从i到i+2^{(j-1)-1为一段，i+2}(j-1)到i+2^{j-1为一段(长度都为2}（j-1）)。用上例说明，当i=1，j=3时就是3,2,4,5 和 6,8,1,2这两段。F[i，j]就是这两段的最大值中的最大值。于是我们得到了动态规划方程F[i, j]=max（F[i，j-1], F[i + 2^(j-1)，j-1]）。

然后是查询。取k=[log2(j-i+1)]，则有：RMQ(A, i, j)=min{F[i,k],F[j-2^k+1,k]}。举例说明，要求区间[2，8]的最大值，就要把它分成[2,5]和[5,8]两个区间，因为这两个区间的最大值我们可以直接由f[2，2]和f[5，2]得到。

算法伪代码：
//初始化
INIT_RMQ
//max[i][j]中存的是重j开始的2^i个数据中的最大值，最小值类似，num中存有数组的值
for i : 1 to n
  max[0][i] = num[i]
for i : 1 to log(n)/log(2)
  for j : 1 to (n+1-2^i)
     max[i][j] = MAX(max[i-1][j], max[i-1][j+2^(i-1)]
//查询
RMQ(i, j)
k = log(j-i+1) / log(2)
return MAX(max[k][i], max[k][j-2^k+1])

LCA算法

对于该问题，最容易想到的算法是分别从节点u和v回溯到根节点，获取u和v到根节点的路径P1，P2，其中P1和P2可以看成两条单链表，这就转换成常见的一道面试题：【判断两个单链表是否相交，如果相交，给出相交的第一个点。该算法总的复杂度是O（n）（其中n是树节点个数）
在线算法DFS+ST描述(思想是：将树看成一个无向图，u和v的公共祖先一定在u与v之间的最短路径上)：

（1）DFS：从树T的根开始，进行深度优先遍历（将树T看成一个无向图），并记录下每次到达的顶点。第一个的结点是root(T)，每经过一条边都记录它的端点。由于每条边恰好经过2次，因此一共记录了2n-1个结点，用E[1, … , 2n-1]来表示。

（2）计算R：用R[i]表示E数组中第一个值为i的元素下标，即如果R[u] < R[v]时，DFS访问的顺序是E[R[u], R[u]+1, …, R[v]]。虽然其中包含u的后代，但深度最小的还是u与v的公共祖先。

（3）RMQ：当R[u] ≥ R[v]时，LCA[T, u, v] = RMQ(L, R[v], R[u])；否则LCA[T, u, v] = RMQ(L, R[u], R[v])，计算RMQ。

由于RMQ中使用的ST算法是在线算法，所以这个算法也是在线算法。
图论--最近公共祖先LCA

例题：
7 6 7个数6条边
3 7
3 4
4 5
4 6
5 1
6 2
求2和7的lca.
假如我们要询问 2 和7 的 LCA, 我们找到2和7 分别第一次出现的位置, 然后在这一个区间内找到深度最小的那个节点, 也就是节点 3, 显然它就是2 和7的 LCA.
图论--最近公共祖先LCA

#include<iostream>
#include<cstdio>
#include<cmath>
using namespace std;
int n,m,cnt,tot=0,x,y,head[505],vis[505],dfn[505],de[505],ofs[505],dp[505][9],ru[505],root;
struct Egde{
    int to,next;
}edge[505];//表示边 
void add_edge(int bg,int ed)
{
    cnt++;
    edge[cnt].to=ed;
    edge[cnt].next=head[bg];
    head[bg]=cnt;
}
void dfs(int u,int dep)
{
    tot++;
    if(!vis[u]){
        vis[u]=1;dfn[u]=tot;
    }
    de[tot]=dep;
    ofs[tot]=u;
    for(int e=head[u];e>0;e=edge[e].next)
    {
        int v=edge[e].to;
        dfs(v,dep+1);
        ofs[++tot]=u;//通过这句话tot加,使dfn[]增加
    }
}
void init()//dp[]表示哪个tot
{
    for(int j=0;(1<<j)<=tot;j++)
    {
        for(int i=1;i+(1<<j)<=tot;i++)
        {
            if(j==0) dp[i][j]=i;
            else //dp用来存从i开始的2的j次方个区间内的最小值 
            {
                if(de[dp[i][j-1]]<de[dp[i+(1<<(j-1))][j-1]])
                    dp[i][j]=dp[i][j-1];
                else dp[i][j]=dp[i+(1<<(j-1))][j-1];//注意这里的左移外括号 
            }
        }
    }
}
int RMQ(int p1,int p2)//p1,p2是位置 
{
    int k=0;
    k=log2(p2-p1+1);
    if(de[dp[p1][k]]<de[dp[p2-(1<<k)+1][k]])
        return ofs[dp[p1][k]];
    else return ofs[dp[p2-(1<<k)+1][k]];
}
int lca(int v1,int v2)
{
    if(dfn[v1]<dfn[v2]) return RMQ(dfn[v1],dfn[v2]);//4,12 
    else RMQ(dfn[v2],dfn[v1]);
}
int main()
{
    scanf("%d%d",&n,&m);
    for(int i=1;i<=m;i++)
    {
        scanf("%d%d",&x,&y);
        add_edge(x,y);
        ru[y]++;
    }
    for(int i=1;i<=n;i++)if(ru[i]==0) root=i;
    dfs(root,1);
    init();
//  for(int i=1;i<=n;i++) 
//      for(int j=head[i];j>0;j=edge[j].next)
//          cout<<edge[j].to<<":"<<dfn[edge[j].to]<<" ";
//  cout<<endl;
    cout<<lca(2,7)<<endl;
}

裸求LCA

假设目前求点u和v的最近公共祖先。
1、首先找到两点中深度较深的点（在树上的深度越深代表其越往下），不妨设深度较深的结点为u，不停的将u往上提，直到u的深度和v一样。
2、同时将u和v向上提，直到u和v变成了同一个点。这个点就是要求的醉经公共祖先。

#include<bits/stdc++.h>
using namespace std;
const int N = 1e6+10;
int fa[N],d[N],n,m,rt;
vector<int>G[N];
void add(int u,int v)
{
	G[u].push_back(v);
	G[v].push_back(u);
 } 
void dfs(int u)//先计算每个点的深度
{
	for(int i = 0;i<G[u].size();i++)
	{
		int v = G[u][i];
		if(v==fa[u]) continue;
		fa[v]=u;//保存每个点的父节点 
		d[v]=d[u]+1;//子节点的深度比父节点多1
		dfs(v);
	}
 } 
 int LCA(int u,int v)
 {
 	if(d[u]<d[v]) swap(u,v);//找出深度最深的点，保存在u中
 	while(d[u]!=d[v]) u= fa[u];//先不停的让u变成它的父节点，往上提直到同一层
 	while(u!=v)
 	{
 		u=fa[u];
 		v=fa[v];
 		//之后再不断地同时往上提u,v，直到它们相同之后，这个点就是答案
	 }
	 return u;
 }
 int main()
 {
 	cin>>n>>m>>rt;
 	for(int i = 1;i<n;i++)
 	{
 		int u,v;
 		cin>>u>>v;
 		add(u,v);
	 }
	 dfs(rt);
	 for(int i = 1;i<=m;i++)
	 {
	 	int u,v;
	 	cin>>u>>v;
	 	cout<<LCA(u,v)<<endl;
	 }
 }

这个程序虽然正确计算了样例，但会超时。分析程序会发现，每次询问最近公共祖先的时候最坏的情况是爬完整棵树（想象一条链的情况）,所以每次询问的时间复杂度是O(n)的。

倍增求LCA

图论--最近公共祖先LCA

以 17 和 18 为例，既然要求LCA，那么我们就让他们一个一个向上爬(我要一步一步往上爬 —— 《蜗牛》)，直到相遇为止。第一次相遇即是他们的LCA。模拟一下就是：
17->14->10->7->3
18->16->12->8->5->3
最终结果就是 3。

倍增算法

所谓倍增，就是按2的倍数来增大，也就是跳1,2,4,8,16,32 …… 不过在这我们不是按从小到大跳，而是从大向小跳，即按……32,16,8,4,2,1来跳，如果大的跳不过去，再把它调小。这是因为从小开始跳，可能会出现“悔棋”的现象。拿 5 为例，从小向大跳，5≠1+2+4,所以我们还要回溯一步，然后才能得出5=1+4；而从大向小跳，直接可以得出5=4+5=4+1。这也可以拿二进制为例，5(101)，从高位向低位填很简单，如果填了这位之后比原数大了，那我就不填，这个过程是很好操作的。

还是以 17 和 18 为例（此例只演示倍增，并不是倍增LCA算法的真正路径）：
17->3
18->5->3
可以看出向上跳的次数大大减小。这个算法的时间复杂度为O(nlogn),已经可以满足大部分的需求。

想要实现这个算法，首先我们要记录各个点的深度和他们2^i
级的的祖先，用数组depth[]表示每个节点的深度，fa[i][j]表示节点i的2^j级祖先。代码如下：

void dfs(int f,int fath) //f表示当前节点，fath表示它的父亲节点
{
depth[f]=depth[fath]+1;
fa[f][0]=fath;
for(int i=1;(1<<i)<=depth[f];i++)
  fa[f][i]=fa[fa[f][i-1]][i-1]; //这个转移可以说是算法的核心之一
                                //意思是f的2^i祖先等于f的2^(i-1)祖先的2^(i-1)祖先
                                //2^i=2^(i-1)+2^(i-1)
for(int i=head[f];i;i=e[i].nex)
  if(e[i].t!=fath)
    dfs(e[i].t,f);
}

预处理完毕后，我们就可以去找它的LCA了，为了让它跑得快一些，我们可以加一个常数优化。

for(int i=1;i<=n;i++) //预先算出log_2(i)+1的值，用的时候直接调用就可以了
  lg[i]=lg[i-1]+(1<<lg[i-1]==i);  //看不懂的可以手推一下

接下来就是倍增LCA了，我们先把两个点提到同一高度，再统一开始跳。

但我们在跳的时候不能直接跳到它们的LCA，因为这可能会误判，比如4和8，在跳的时候，我们可能会认为1是它们的LCA，但1只是它们的祖先，它们的LCA其实是3。所以我们要跳到它们LCA的下面一层，比如4和8，我们就跳到4和5，然后输出它们的父节点，这样就不会误判了。

int lca(int x,int y)
{
if(depth[x]<depth[y]) //用数学语言来说就是：不妨设x的深度 >= y的深度
  swap(x,y);
while(depth[x]>depth[y])
  x=fa[x][lg[depth[x]-depth[y]]-1]; //先跳到同一深度
if(x==y)  //如果x是y的祖先，那他们的LCA肯定就是x了
  return x;
for(int k=lg[depth[x]]-1;k>=0;k--) //不断向上跳（lg就是之前说的常数优化）
  if(fa[x][k]!=fa[y][k])  //因为我们要跳到它们LCA的下面一层，所以它们肯定不相等，如果不相等就跳过去。
    x=fa[x][k], y=fa[y][k];
return fa[x][0];  //返回父节点
}

完整的求17和18的LCA的路径：
17->10->7->3
18->16->8->5->3
解释：首先，18要跳到和17深度相同，然后18和17一起向上跳，一直跳到LCA的下一层(17是7，18是5)，此时LCA就是它们的父亲。

Tarjan求LCA

Tarjan

int f[maxn],fs[maxn];//并查集父节点 父节点个数
bool vit[maxn];
int anc[maxn];//祖先
vector<int> son[maxn];//保存树
vector<int> qes[maxn];//保存查询
typedef vector<int>::iterator IT;
 
int Find(int x)
{
    if(f[x]==x) return x;
    else return f[x]=Find(f[x]);
}
void Union(int x,int y)
{
    x=Find(x);y=Find(y);
    if(x==y) return;
    if(fs[x]<=fs[y]) f[x]=y,fs[y]+=fs[x];
    else f[y]=x,fs[x]+=fs[y];
}
 
void lca(int u)
{
    anc[u]=u;
    for(IT v=son[u].begin();v!=son[u].end();++v)
    {
        lca(*v);
        Union(u,*v);
        anc[Find(u)]=u;
    }
    vit[u]=true;
    for(IT v=qes[u].begin();v!=qes[u].end();++v)
    {
        if(vit[*v])
            printf("LCA(%d,%d):%d\n",u,*v,anc[Find(*v)]);
    }
}