密码学:公钥密码.
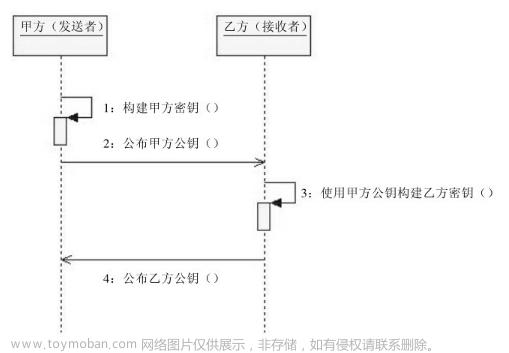
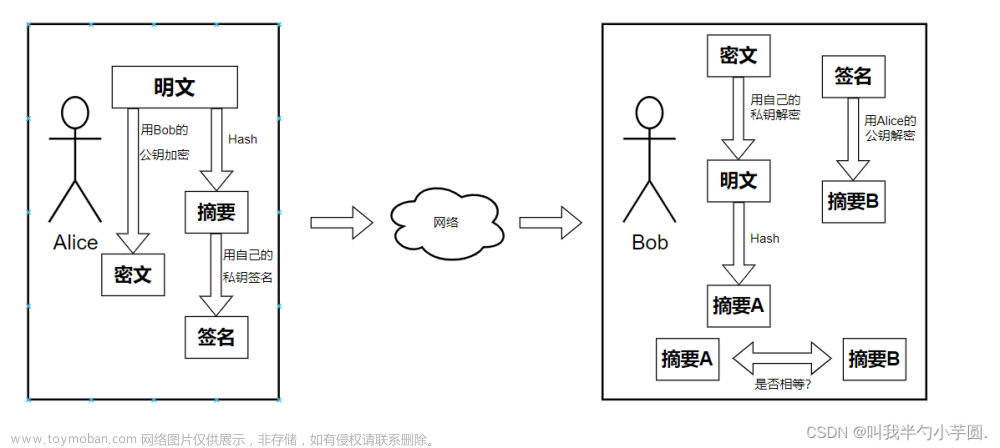
公钥密码 (Public Key Cryptography),又称为非对称密码,其最大特征是加密和解密不再使用相同的密钥,而使用不同的密钥。使用者会将一个密钥公开,而将另一个密钥私人持有,这时这两个密钥被称为公钥和私钥。一般来说,公钥和私钥是难以互相计算的,但它们可以互相分别作为加密密明和解密密钥。当信息发送者选择采用接收者的公钥加密时,接收者收到信息后使用自己的私钥解密,这样便可保持信息的机密性;若信息发送者使用自己的私钥对信息摘要进行加密,接收者使用发送者的公钥对摘要进行验证,即可起到签名的作用,可以保证信息的认证性和不可否认性。
目录:
密码学:公钥密码
RSA算法:
RSA的常见攻击:
(1)因式分解:
(2)低加密指数小明文攻击
(3)共模攻击
(4)广播攻击
(5)低解容指数攻击 (Wiener's Attack)
(6)Coppersmith's High Bits Attack
(7)RSA LSB Oracle
离散对数相关密码学:
(1)EIGamal和ECC
(2)离散对数的计算
1.暴力计算
2.更高效的计算方法
RSA算法:
RSA 算法是目前工程中使用最广泛的公钥密码算法,算法的安全性基于一个简单的数学事实: 对于大素数 p 和 q,计算 n = pxq 非常简单,但是在已知 n 的情况下分解因子得到 p 和 q 则相当困难。
在线RSA算法加密和解密:RSA在线加密解密 - RSA密钥生成器
RSA的基本算法如下: 选取较大的索数 p 和 q(一般大于 512bit,且 p 不等于 q),计算:
n = p x q
该加解密算法的正确性证明如下:

所以:

RSA的常见攻击:
(1)因式分解:
由于 RSA 的私钥生成过程中只用到了p、g与e,如果p、q被成功求出,那么可使用正常的计算方法将私钥模数 d 算出。如果 n 的大小不太大 (不大于 512 位),建议先行尝试因式分解法。因式分解时常用的辅助工具有 SageMath 、Yafu,以及在线因子查询网站 factordb。 另外,若p和9的差距非常小,由于

即可通过暴力枚举 p - g 的值来分解pq。
例如,对于 RSA 公钥<n,e>=<16422644908304291,65537>,由于的值较小,可以考虑使用因式分解的方法。使用 Yafu 执行 factor (16422644908304291),得到以下输出:

从而得到两个素数 p 和 q 分别为 134235139 和 122342369 。使用Gmpy2 Python库可以计算出私钥 a 的值。

(2)低加密指数小明文攻击
如果被加密的 m 非常小,而且 e 较小,导致加密后的 c 仍然小于 n,那么便可对密文直接开 e 次方,即可获得明文 m。例如,考虑以下情况: n=100000980001501,e=3,m=233,那么pow (m,e) =12649337,仍然小于n。此时,对12649337开3次方即可解出明文233.
如果加密后的 c 虽然大于 n 但是并不太大,由于pow (m,e) =kn+c,可以暴力枚举 k,然后开 e 次方,直到 e 次方可以开尽,解出了正确的 C 为止。例如,当 r 和 e 与上式相同,但 m =233333时,有 C = pow(m,e,n) =3524799146410。
使用 Python 枚举n的系数的代码如下:

当枚举到 k=127 时,3次方可以开尽,解得明文为233333;
(3)共模攻击
如果使用了相同的n,不同的模数e1、 e2,且e1、e2互素,对同一组明文进行加密,得到密文c1、c2那么可以在不计算私钥的情况下计算出明文 m。设


显然,对相同的m使用同一个n和不同的e加密得到了不同的c,且两个e互素,可以尝试用共模攻击的方法解出m。
首先,使用扩展欧几里得算法求出xe1+ye2=1中的x和y:



即可在不分解n的情况下解得明文m。由于扩展欧几里得算法的时间复杂度为O(logn),在n非常大
时,该方法仍然可用。
如果遇到只有一组明文但被多个e加密得到了多个密文的情况,应该先考虑使用共模攻击。
(4)广播攻击
对于相同的明文m,使用相同的指数e和不同的模数n1,n2,···,ni,加密得到i组密文时(i ≥ e),可以使用中国剩余定理解出明文。设

联立方程组,使用中国剩余定理,可以求得一个Cx满足


下面尝试使用广播攻击来解出n。联立三个方程组,使用中国剩余定理:

可以看到,我们成功解出了明文.
若看到使用相同的e不同的n进行了多次加密且e较小,密文组数不小于e组,应当考虑使用此方法。
(5)低解容指数攻击 (Wiener's Attack)

(6)Coppersmith's High Bits Attack
本方法由Don Coppersmith提出,如果已知明文的很大部分,即m=motx,已知mo或组成n中一个大素数的高位,就可以对私钥进行攻击。一般,对于1024位的大素数,只需要知道640位即可成功攻击。攻击的详细实现见:GitHub - mimoo/RSA-and-LLL-attacks: attacking RSA via lattice reductions (LLL)
(7)RSA LSB Oracle



离散对数相关密码学:
(1)EIGamal和ECC


(2)离散对数的计算
1.暴力计算
当 p 的值不太大时,由于离散对数的取值一定在0 ~p-1范围内,显然可以暴力穷举。例如,考虑以下情况:

可以写出以下暴力计算代码:

以下是椭圆曲线离散对数的暴力破解示例。考虑如下曲线和点,求logpQ:

在Sagemath中定义该圆曲线和P、Q两个点,写出循环,即可进行暴力破解:

该方法的时间复杂度为O (n) ,当p小于1e7数量级时,暴力计算是可以考虑的。
2.更高效的计算方法
Sagemath内置了不同种类的离散对数计算方法,适用于各种场合。以下代码介绍了一些常用的计算离散对数的算法,具体使用条件等请参考代码注释。

好用的解密网站:在线AES加密解密、AES在线加密解密、AES encryption and decryption--查错网
文章来源:https://www.toymoban.com/news/detail-436333.html
学习书籍:从0到1:CTFer成长之路... 文章来源地址https://www.toymoban.com/news/detail-436333.html
到了这里,关于密码学:公钥密码.(非对称密码)的文章就介绍完了。如果您还想了解更多内容,请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章,希望大家以后多多支持TOY模板网!