目录
1.时间和空间复杂度
1.1时间复杂度
1.2空间复杂度
2.包装类
2.1基本数据类型和对应的包装类
2.2装箱和拆箱
//阿里巴巴面试题
3.泛型
3.1擦除机制
3.2泛型的上界
1.时间和空间复杂度
1.1时间复杂度
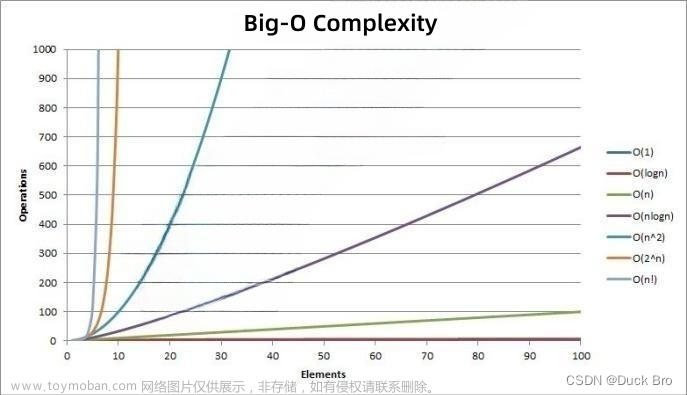
定义:一个算法所花费的时间与其语句的执行次数成正比,算法中的基本操作的执行次数,为算法的时间复杂度。
public class Main {
public static void main(String[] args) {
int n = 10;
int count = 0;
for (int i = 0; i < n; i++) {
for (int j = 0; j < n; j++) {
count++; //F(n)=n^2
}
}
for (int k = 0; k < 2*n; k++) {
count++; //F(n)=2n
}
for (int m = 0; m < 10; m++) {
count++; //F(n)=10
}
}
}所以此时F(n)=n^2+2n+10, 但实际情况下只需要计算大概执行次数,即——大O渐进法:
大O渐进法:
1> 用常数1代替所有的加法常数;
2> 只保留最高阶项;
3> 如果最高阶项存在且不是1,则去除与这个项相乘的常数。
例:F(n) = 2n^2 + 5n + 100 = O(n^2)
注意:
二分查找 O(n) = log2N
递归 O(n) = 递归的次数*每次递归后执行的次数
public class Main {
long factorial(int n) { //阶乘
return n<2?n:factorial(n-1)*n; //O(n)=n
}
long fibonacci(int n) { //菲波那切数列
return n<2?n:factorial(n-1)+factorial(n-2); //O(n)=2^n
}
}拓展:平均复杂度
定义:所有情况下代码执行的次数累加起来,再除以所有情况数量,即为平均复杂度。
例如下述代码,判断x在循环中出现的位置,有n+1种情况:1<=x<=n 和 n<x,
所以平均复杂度为=((1+2+3+……+n) + n)/ n+1
public int Function(int n, int x)
{
int sum = 0;
for (int i = 1; i <= n; ++i)
{
if (i == x)
break;
sum += i;
}
return sum;
}1.2空间复杂度
定义:空间复杂度是一个算法在运行时临时占用存储空间大小的量度,即计算的是变量的个数。
public class Test {
//实例1:使用了常数个额外空间,空间复杂度为O(1)
//冒泡排序
void bubbleSort(int[] array) {
for (int end = array.length; end > 0; end--) {
boolean sorted = true;
for (int i = 1; i < end; i++) {
if (array[i - 1] > array[i]) {
Swap(array, i - 1, i);
sorted = false;
}
} if
(sorted == true) {
break;
}
}
}
//实例2:动态开辟了N个空间,空间复杂度为O(N)
//菲波那切数列
long[] fibonacci(int n) {
long[] fibArray = new long[n + 1];
fibArray[0] = 0;
fibArray[1] = 1;
for (int i = 2; i <= n ; i++) {
fibArray[i] = fibArray[i - 1] + fibArray [i - 2];
}
return fibArray;
}
//实例3:递归调用了N次,开辟了N个栈帧,每个栈帧使用了常数个空间,空间复杂度为O(N)
//阶乘递归
long factorial(int N) {
return N < 2 ? N : factorial(N-1)*N;
}
}
2.包装类
2.1基本数据类型和对应的包装类
| 基本数据类型 |
包装类 |
|---|---|
| byte | Byte |
| short | Short |
| int | Integer |
| long | Long |
| float | Float |
| double |
Double |
| char | Character |
| boolean | Boolean |
2.2装箱和拆箱
装箱:基本类型——>包装类型
拆箱:包装类型——>基本类型
public class Test {
public static void main(String[] args) {
int a = 10;
Integer i = a;//自动装箱
Integer ii = new Integer(a);//显示装箱
Integer iii = new Integer(a);//显示装箱
int m = i.intValue();//显示拆箱
float ff = i.intValue();//拆成对应的类型
int fff = a;//自动拆箱
}
}//阿里巴巴面试题
public class Test {
public static void main(String[] args) {
Integer a = 127;
Integer b = 127;
Integer c = 128;
Integer d = 128;
System.out.println(a==b);//true
System.out.println(c==d);//false
}
}原因:装箱时底层调用了valueOf方法,本质是一个范围在-128~127之间的数组。
3.泛型
先来看看一道编程题,编程要求:创建一个可以存放任何类型数据的数组。
解:所有类的父类默认为Object类,所以可以创建一个Object数组用来存放不同类型的元素:
class MyArray {
public Object[] objects = new Object[10];//创建Object类数组
public Object getPos(int pos) {//访问数组
return objects[pos];
}
public void setVal(int pos,Object val) {//赋值数组
objects[pos] = val;
}
}
public class Test {
public static void main(String[] args) {
MyArray myArray = new MyArray();
//此时可以将不同类型的元素放入数组中
myArray.setVal(0,"123");
myArray.setVal(1,10);
//由于父类是Object类型,访问时必须强制类型转换
int val = (int)myArray.getPos(1);
System.out.println(val);//10
}
}
我们发现上述代码有些繁琐,但用泛型来解这道题就会简单可读很多:
定义:通俗来讲,就是适用于许多许多类型,从代码上讲,就是对类型实现了参数化(传递类型)。
意义:在编译时帮我们进行类型的检查和转换,注意在运行时没有泛型这一概念,即JVM中没有泛型。
语法:class 泛型类名称 <类型形参列表> { 代码块 }
常见类型形参列表:E - Element、K - Key、V - Value、N - Number、T - Type、S/U/V等 - 第二、第三、第四个类型。
注意:不能new泛型类型的数组。
class MyArray <T> { //T是一个占位符,表示当前类是一个泛型类
public T[] objects = (T[]) new Object[10];//这种写法不是很好,改良版见下
public T getPos(int pos) {
return objects[pos];
}
public void setVal(int pos,T val) {
objects[pos] = val;
}
}
public class Test1 {
public static void main(String[] args) {
MyArray<Integer> myArray1 = new MyArray<Integer>();//指定类型为Integer
myArray1.setVal(0,1); //这里的Integer可不写
myArray1.setVal(1,2);
int val = myArray1.getPos(1);
System.out.println(val);//2
MyArray<String> myArray2 = new MyArray<String>();//指定类型为String
myArray2.setVal(0,"hello"); //这里的String可不写
myArray2.setVal(1,"world");
String ret = myArray2.getPos(1);
System.out.println(ret);//world
}
}3.1擦除机制
定义:在编译过程中,将所有的T替换为Object,这种机制称为擦除机制。
编译器生成的字节码在运行期间并不包含泛型的类型信息。
class MyArray <T> {
public Object[] objects =new Object[10];
public T getPos(int pos) {
return (T)objects[pos];//强转
}
public void setVal(int pos,Object val) {
objects[pos] = val;
}
}3.2泛型的上界
写一个泛型类,其中有个方法,用来求数组中的最大值:
class Alg<T extends Comparable<T>> { //擦除为一个实现了Comparable接口的类型
public T findMax(T[] array) { //即限制了T的边界(上界),使其为Comparable的子类或Comparable本身
T max = array[0];
for (int i = 1; i < array.length; i++) {
if(max.compareTo(array[i]) < 0) {
max = array[i];
}
}
return max;
}
}
class Alg2 {
public static<T extends Comparable<T>> T findMax(T[] array) { //静态泛型方法
T max = array[0];
for (int i = 1; i < array.length; i++) {
if(max.compareTo(array[i]) < 0) {
max = array[i];
}
}
return max;
}
}
public class Test {
public static void main(String[] args) {
Alg<Integer> alg = new Alg<>();
Integer[] array = {1,9,3,7,5,4};
Integer max = alg.<Integer>findMax(array);//此处Integer可不写
System.out.println(max);
}
public static void main2(String[] args) {
Integer[] array = {1,9,3,7,5,4};
Integer max = Alg2.<Integer>findMax(array);//此处Integer可不写
System.out.println(max); //静态方法通过类名调用
}
}这一点点只是开胃菜,后面还有更多有趣的知识等着我们去学习!文章来源:https://www.toymoban.com/news/detail-436403.html
痛并快乐着捏 ~ ~ 文章来源地址https://www.toymoban.com/news/detail-436403.html
到了这里,关于【数据结构】复杂度&包装&泛型的文章就介绍完了。如果您还想了解更多内容,请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章,希望大家以后多多支持TOY模板网!