数据结构与算法基础（青岛大学-王卓）(1)

士别三日当刮目相待，不好意思鸽了好久了，因为学习的时间不连续，所以我一直攒着，我又回来继续更新了

没有继续学习浙大的数据结构了，对比了青岛大学的王老师的这个教程我觉得更适合我一些，更入门，更详细。

课程连接：数据结构与算法基础（青岛大学-王卓）

下面是整理的第一部分笔记，有些地方直接用截图了(偷懒ing)

Data Structure

程序=数据结构+算法

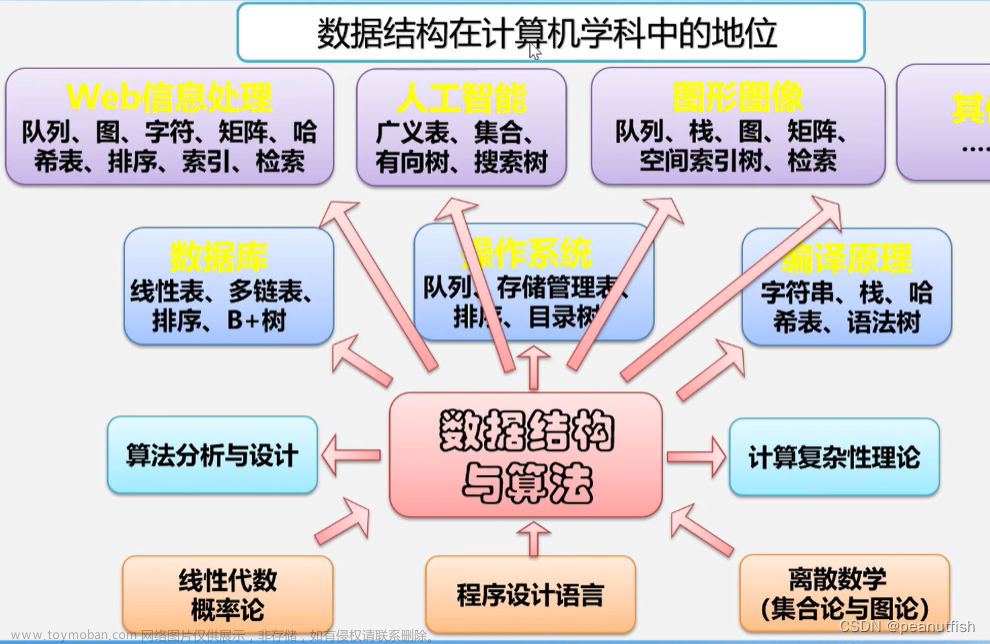
数据基本概念

数据(data)

• 数值型
• 非数值型(文字，图像…)

数据元素(data element)

• 数据的基本单位，在程序中当做一个整体进行考虑和处理(如表中的一行包含多列信息)
• 是数据这个集合的个体

数据项(data item)

• 构成数据元素的不可分割的最小单位()
  

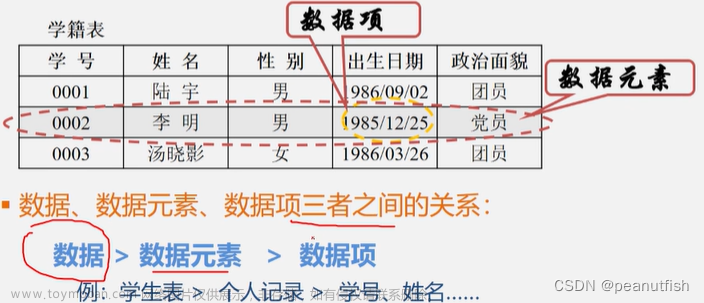
数据对象(data object)

• 性质相同的数据元素的集合，是数据(集合)的一个子集。

数据结构(data structure)定义

• 数据元素之间的关系称为结构

• 相互之间存在一种或者多种特定关系的数据元素集合

• 数据结构是带结构的数据元素的集合

是计算机中存储，组织数据的方法。通常情况下，精心选择的数据结构可以带来最有效率的算法。

解决问题的效率跟 数据的组织方式, 跟空间的利用率, 算法的巧妙程度有关。

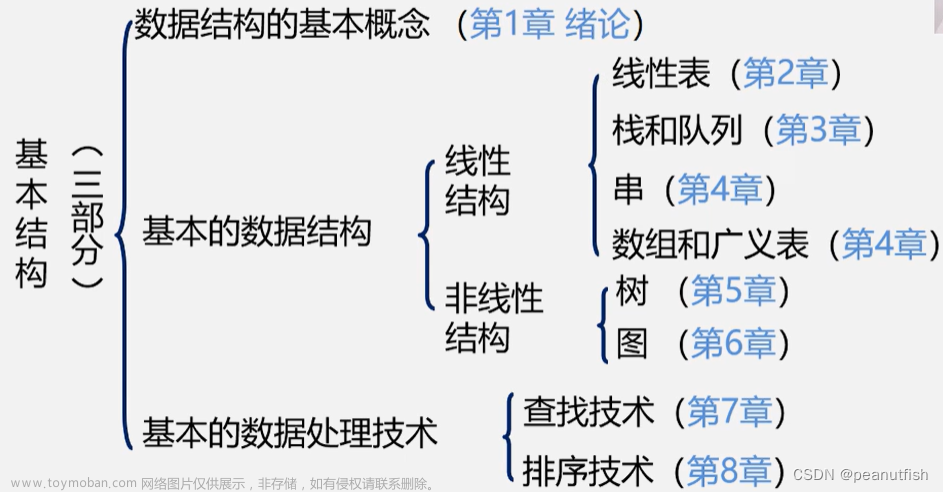
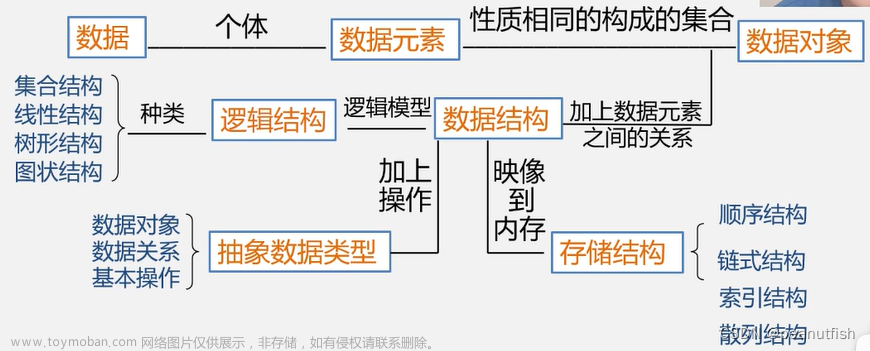
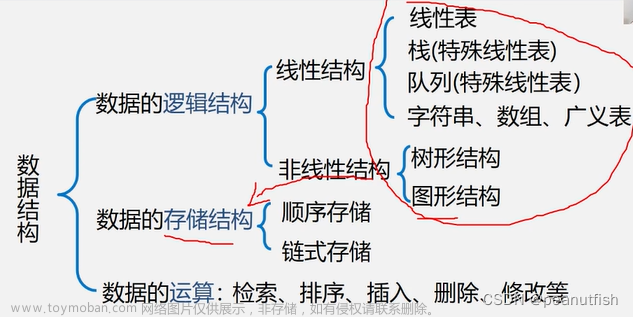
数据逻辑结构

划分方法一：

• 线性结构(有且仅有一个开始和一个终端节点，并且所有节点最多只有一个直接前趋和一个直接后继， 如线性表，栈，队列，串)
• 非线性结构(一个节点可能有多个直接前趋和多个直接后继，如树，图)

划分方法二

• 集合结构(除同属一个集合外无其他关系)
• 线性结构(一对一)
• 树形结构(一对多的层次关系)
• 图状结构或网状结构(多对多)

数据存储结构种类

• 顺序存储(一组联系的存储单元依次存储数据元素，C中用数组来实现顺序存储)
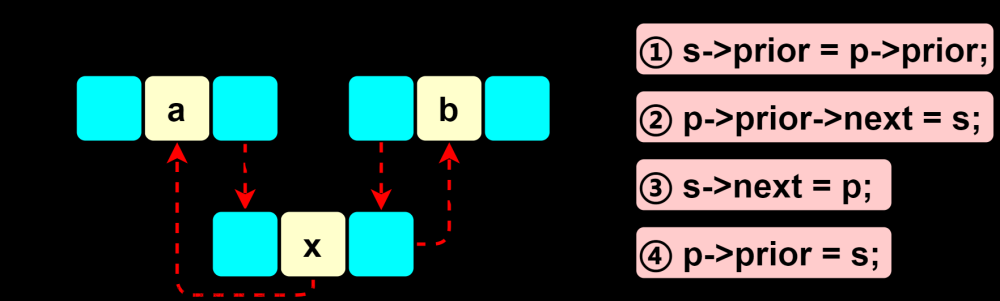
• 链式存储(一组任意的存储单元存储元素，之间的逻辑关系用指针表示, C中用指针实现，前一个元素包含后一个元素的指针位置)
• 索引存储(存储节点信息的同时还建立附加的索引表，索引项-关键字-地址)
• 散列存储(根据节点的关键字直接计算出该节点的存储地址)

数据类型

• 使用高级语言编写程序时，必须对程序中出现的每个变量常量，表达式，明确说明他们的数据类型，如c中

  • int,char,float,double等基本数据类型
  • 数组，结构，共用体，枚举等构造数据类型
  • 指针，void类型
  • typedef自定义类型

• 数据类型作用：约束变量或者常量的取值范围，以及操作。eg: int(-65536, 65535) + - * /

• 定义：是一组性质相同的值的集合以及定义于这个值的集合上的一组操作的总称

• 抽象数据类型(Abstract Data Type, ADT): 指一个数字模型以及定义在此数据模型上的一组操作

  • 形式定义：

    ADT 抽象数据类型名{
    	数据对象:<数据对象的定义>
    	数据关系:<数据关系的定义>
    	数据操作:<基本操作的定义>
    } ADT 抽象数据类型名
    
    # 参数表说明：赋值参数，引用参数(以&打头, 可输入和返回结果)
    基本操作名(参数表)
    初始条件 <初始条件描述>
    操作结果 <操作结果描述>
    
    EG：
    ADT Circle{
    数据对象：D={r,x,y|r,x,Y均为实数}
    数据关系：{<r,x,Y>|r是半径，<x,y>是圆心坐标}
    基本操作:
    Circle(&C,r,x,y)
    	操作结果：构造一个圆。
    double Area(C)
    	初始条件：圆已存在。
    	操作结果：计算面积。
    double Circumference(C)
    	初始条件：圆已存在。
    	操作结果：计算周长。
    ...
    } ADT Circle
    

  • 抽象数据类型的复数的实现

    typede struct{
    	float realpart;
    	float imagpart;
    } Complex
    
    /* 构造复数 */    
    void assign(Complex * A, float real, float imag){
        A->realpart = real;
        A->imagpart = imag
    }
    
    /* 加法c = A+B */
    void add(Complex * c, Complex A, Complex B){
        c->realpart = A.realpart + B.realpart;
        c->imagpart = A.imagpart + B.imagpart;
    }
    
    /* 减法c = A-B */
    /* Complex 是我们定义的结构体，带*的变量是指针变量，指向complex类的指针，不带*的是普通变量 */
    void add(Complex * c, Complex A, Complex B){
        c->realpart = A.realpart - B.realpart;
        c->imagpart = A.imagpart - B.imagpart;
    }
    
    /* 乘法c = A*B */
    void multiply(Complex * c, Complex A, Complex B){
        c->realpart = A.realpart * B.realpart;
        c->imagpart = A.imagpart * B.imagpart;
    }
    
    /* 除法c = A/B */
    /* 真实环境下这里是要先判断除数是否为0的 */
    void devide(Complex * c, Complex A, Complex B){
        c->realpart = A.realpart / B.realpart;
        c->imagpart = A.imagpart / B.imagpart;
    }
    

    how to calculate
    $$z=\frac{(8+6i)(4+3i)}{(8+6i)+(4+3i)}$$

    # include <stdio.h>
    void main()
    {
        complex z1,z2,z3,z4,z;
        float RealPart, ImagPart;
        assign(z1, 8.0, 6.0);
        assign(z2, 4,0, 3.0);
        add(z1,z2,z3);
        multiply(z1,z2,z4);
        if (divide(z4,z3)) {
            GetReal(z, RealPart);
            GetImag(z, ImagPart);
        }//if        
    }
    

• Summary:

算法

算法(algorithm)定义

• 对特定问题求解方法的一种描述，是指令的有限序列。其中每个指令表示一个或多个操作。（简而言之，算法是解决问题的方法和步骤）

• 描述方法：自然语言(中英)，流程图(传统&NS流程图)，伪代码，程序代码

• 算法和程序的关系：算法是解决问题的一种方法或者一个过程，程序时用高级语言对算法的具体实现

• 算法特性：

  • 有穷性: 执行有穷步，有穷时间完成

  • 确定性：每一条命令有确切的含义

  • 可行性：可执行的

  • 输入：有零个或者多个输入

  • 输出：有一个或者多个输出

• **空间复杂度S(n) 一 根据算法写成的程序在执行时占用存储单元的长度。**这个长度往往与输入数据的规模有关。空间复杂度过高的算法可能导致使用的内存超限，造成程序非正常中断。

• **时间复杂度T(n) 一 根据算法写成的程序在执行时耗费时间的长度。**这个长度往往也与输入数据的规模有关。时间复杂度过高的低效算法可能导致我们在有生之年都等不到运行结果。

空间复杂度例子：

比如下面这个递归实现的函数，如果N特别大，那么每次调用的PrintN都会先把所有东西存在内存，然后等下个执行，这样会导致很容易就吃完了内存，最后直接终止掉了，而通过普通循环实现函数，无论N多大始终只有一个函数，所以没问题。

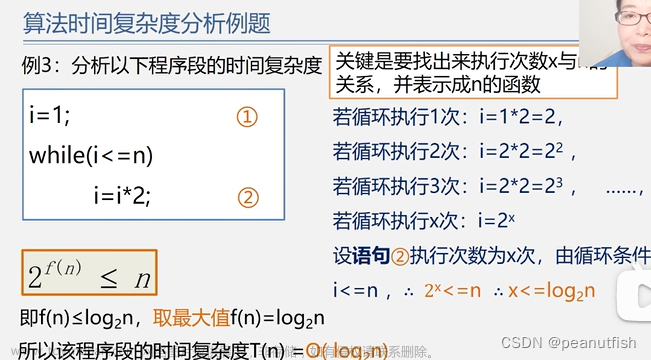
时间复杂度例子：

下面是两个多项式求和公式f(x)=a0+a1X+a2X^2+a3X^3+....a(n-1)X^(n-1)+anX^n

在运算中，加减法的速度远快于乘除法，所以下面的程序我们关注乘法，第一个程序中每次for循环都会执行(pow函数执行i-1次乘法，a[i]执行一次)i次乘法，所以总的次数为(n+1)n/2次乘法，而第二种每 次for循环只执行一次乘法，所以总共n次，这样就可以知道第二种方法在N很大时候耗时更少，在时间复杂度上占优。

什么是好的算法：

分析一般算法效率时关注：

• 最坏情况复杂度Tworst(n)
• 平均复杂度Tavg(n)
• Tavg(n)<=Tworst(n)

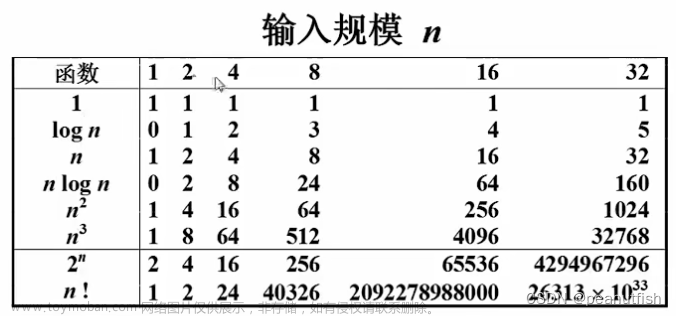
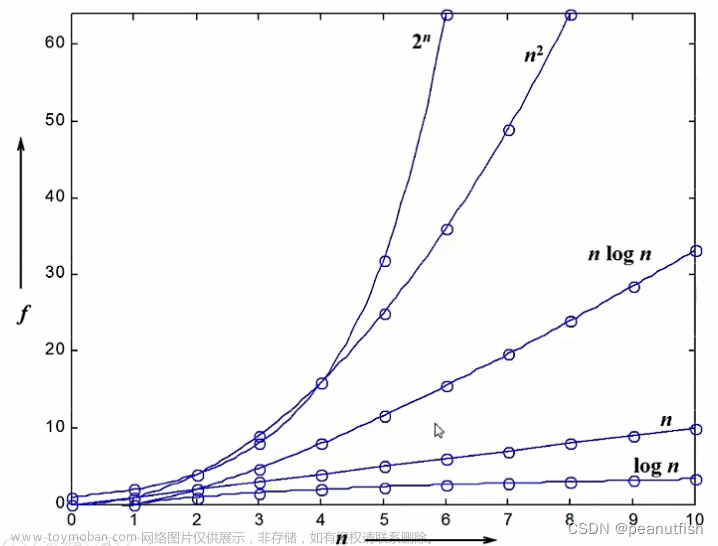
复杂度的渐进表示法：

算法时间复杂度定义：算法中基本语句重复执行的次数是问题规模n的某个函数f(n),算法的时间量度：T(n)=O(f(n)) --> 渐进时间复杂度(T(n)增长率和f(n)的增长率一致 )

n越大算法的执行时间越长

排序：n为记录数

矩阵：n为矩阵的阶数

多项式：n为多项式的项数

集合：n为元素个数

树：n为树的结点个数

图：n为图的顶点数或边数

线性结构

线性表

线性表是具有相同特性的数据元素的一个有限序列。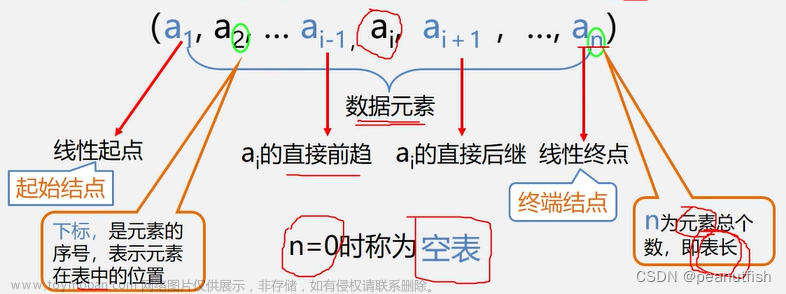

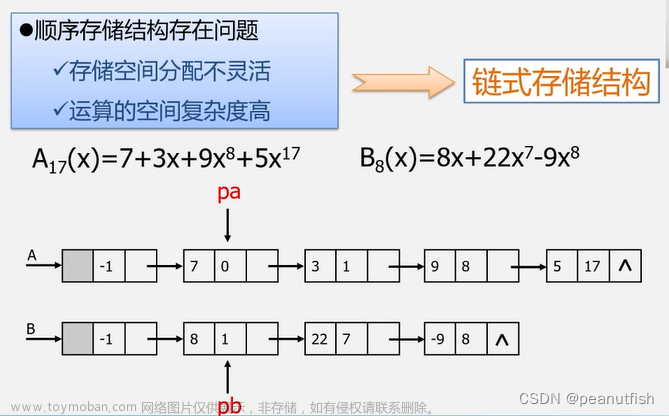
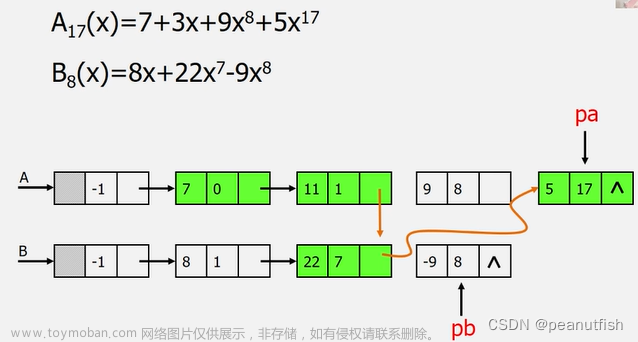
线性表的类型定义

抽象数据类型的线性表定义如下:

ADT List{
	数据对象：D={ai|ai属于Elemset,(i=1,2,...,n>=0)}
	数据关系：R={<ai-l,ai>|ai-l,ai属于D,(i=2,3,...,n)}
	基本操作:
	InitList(&L); # 初始化构造一个空的线性表L
	DestroyList(&L); # 销毁已存在线性表L
    ClearList(&L); # 将线性表L重置为空表
	IsEmpty(L); # 若线性表为空则返回true,否则false 
    ListLength(L); # 返回表中元素个数
    GetElem(L,i,&e); # 用e返回线性表L中第i个元素的值
    LocateElem(L,e,compare()); # 返回L中第一个与e满足comapre()的数据元素的位序，不存在的话返回0
    PriorElem(L,cur_e,&pre_e); # 返回前驱
    NextElem(L,cur_e,&next_e); # 返回后继
    Listlnsert(&L,i,e); # 在L的第i个位置之前插入新的数据元素e,ai变成后继了
	ListDeIete(&L,i,&e); # 删除L中第i各元素，并用e返回
	ListTraverse(&L,visited()); # 依次对线性表中的每个元素调用visited()
}ADT List

线性表的顺序存储表示

顺序存储结构或者顺序映像：把逻辑上相邻的数据元素存储在物理上相邻的存储单元中的存储结构。

• 其中第一个数据元素的a1的存储位置称为基地址(起始位置)

• 存储时地址必须时连续的。

• 所有数据元素的存储位置均可由第一个数据元素的存储位置得到：

  LOC(ai) = LOC(a1) + (i-1)xL (L表示每个元素需占的存储单元)

• 线性表长度可变，但是数组长度不可动态定义(C中 一维数组定义方式：类型说明符 数组名[常量表达式])

• 所以可以用一个变量来表示顺序表的长度属性，定义如下：

  #define LIST_INIT_SIZE 100 //线性表存储空间的初始分配量
  typedef struct{
  	ElemType elem[LIST_INIT_SIZE];
  	int length; //当前长度
  }SqList;
  

  eg: 图书表的顺序存储结构定义

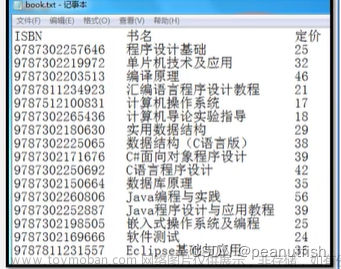
#define MAXSIZE 10000 //图书表可能达到的最大长度

typedef struct{ //图书信息定义
	char no[20]; //图书ISBN
	char name[50]; //图书名字
	float price; //图书价格
}Book;

typedef struct{
	Book *elem; //存储空间的基地址
	int length; //图书表中当前图书个数
}SqList; //图书表的顺序存储结构类型为SqList

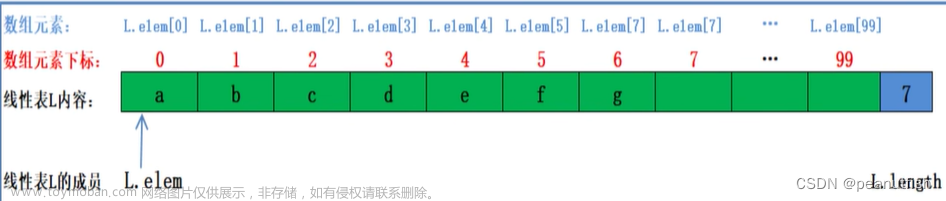
操作算法1

用到的预定义常量和类型：

//函数结果状态代码
#define TRUE  1
#define FALSE 0
#define OK    1
#define ERROR 0
#define INFEASIBLE -1
#define OVERFLOW   -2
//Status 是函数的类型，其值是函数结果状态代码
typedef int Status;
typedef Char ElemType;

• 线性表L的初始化(参数引用)

  StatusInitListSq(SqList&L){ //构造一个空的顺序表L
  	L.elem=new ElemType[MAXSlZE]; //为顺序表分配空间
  	if(!L.elem) exit(OVERFLOW); //存储分配失败
  	L.length=0; //空表长度为0
  	return OK;
  }
  

• 销毁线性表L

  void DestroyList(SqList &L) {
  	if (L.elem) delete L.elem; //释放空间
  }
  

• 清空线性表L

  void ClearList(SqList &L) {
  	L.length=0; //线性表长度置为0
  }
  

• 求线性表L长度和判断L是否为空

  int GetLength(SqList L){
  	return（L.ength);
  }
  
  int IsEmpty(SqList L){
  	if (L.length==0) return 1;
  	else return 0;
  }
  

• 顺序表的取值(根据位置i获取相应位置数据元素的内容)

  int GetElem(SqList L,int i,EIemType &e){
  	if(i<1 || i>L.length) return ERROR;
  //判断i值是否合理，若不合理，返回ERROR
  //第i一1的单元存储着第i个数据
  	e=L.elem[i-1];
  	return OK;
  }
  

操作算法2

• 顺序表的查找

  int LocateELem(SqList L,ElemType e){
  //在线性表L中查找值为e的数据元素，返回其序号（是第几个元素）
  	for(i=0;i<L.length;i++)
  		if(L.elem[i]==e) return i+1; //查找成功，返回序号(下标和序号差一)
  	return0；//查找失败，返回0
  }
  
  int LocateElem(SqList L, ElemType e){
  	i=0;
  	while (i<L.length && L.elem[i]!=e) i++; //查找成功后跳出while循环了
  	if (i < L.length) return i+1;
  	return 0;
  }
  

  • 查找算法分析

    • 平均查找长度ASL(average search length): 为了确定记录在表中的位置，需要与给定值进行比较的关键字的个数的期望值叫做查找算法的ASL。

• 平均查找长度(Pi = 1/n)

  • ASL=p1+2P2+3P3+…(n-1)P(n-1)+nPn=(n+1)/2

• 时间复杂度

  • O(n)

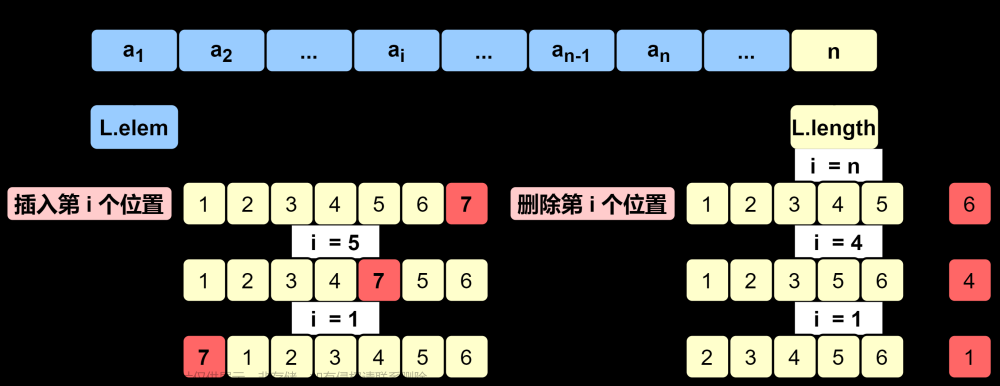
• 顺序表的插入(插入最后，中间，最前，后继元素位置得向后移动，长度随增减)

  Status ListInsert_Sq(SqList &L, int i, ElemType e){
  	if (i<1 || i>L.length+1) return ERROR; //i值不合法
  	if (L.length ==MAXSIZE) return ERROR; //当前存储空间已满
  	for (j=L.length-1;j>=i-1;j--)
  		L.elem[j+1]=L.elem[j] //插入位置及之后的元素后移
  	L.elem[i-1]=e; //新元素e放到第i个位置(下标i-1)
  	L.length++; //表长+1
  	return OK;
  }
  

  • 时间复杂度

    • 插在尾结点，无需移动

    • 插在首节点之前，所有元素后移

    • 插在中间，移动次数为n/2 （出现概率为1/(n+1)）

- O(n)

• 顺序表的删除

  Status ListDelete_Sq(SqList &L, int i, ElemType e){
  	if (i<1 || i>L.length+1) return ERROR; //i值不合法
  	e=L.elem[i-1]; //被删除元素i放到e中
  	for (j=i;j<=L.length-1;j++)
  		L.elem[j-1]=L.elem[j] //插入位置及之后的元素后移
  	L.length--; //表长-1
  	return OK;
  }
  

  • 时间复杂度

    • 平均移动次数

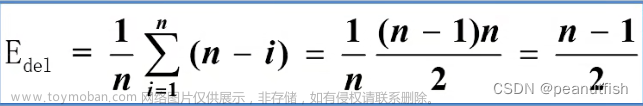
- O(n)

• 以上操作的空间复杂度S(n)=O(1) , 没有占用辅助空间

顺序表的优缺点

优点：
- 存储密度大（结点本身所占存储量/结点结构所占存储量） 
- 可以随机存取表中任一元素 

缺点：（克服缺点用 链表） 
- 在插入、删除某一元素时，需要移动大量元素 
- 浪费存储空间 
- 属于静态存储形式，数据元素的个数不能自由扩充

类C语言的有关操作

数组定义：

//数组静态分配
typedef struct {
	ElemType data[MaxSize]; //存放data[0]位置
	int length;
} SqList;

//数组动态分配
typedef struct {
	ElemType *data; //指针
	int length;
} SqList;

为数组动态分配空间：

SqList;
L.data=(ElemType*)malloc(sizeof(ElemType)*MaxSize);

malloc(m)函数，开辟m字节长度的地址空间，并返回这段空间的首地址sizeof(x)运算，计算变量×的长度
ElemType* 表示分配的空间以什么数据类型进行划分(char/int/float...)
L.data 就是最后得到的基地址

free(p)函数，释放指针p所指变量的存储空间，即彻底删除一个变量 

需要加载头文件：<stdlib.h>

• C++的动态存储分配：

new 类型名T（初值列表）
	功能:
		申请用于存放T类型对象的内存空间，并依初值列表赋以初值
	结果值:
		成功T类型的指针，指向新分配的内存
		失败，0(NULL)

delete 指针P
	功能:
		释放指针P所指向的内存。P必须时new操作的返回值

eg:
int *p1 = new int; //无初值，指针给到p1
或int *pl = new int(10); //初值10

• C++中的参数传递

  • 函数调用时传送给形参表的实参必须与形参三个一致： 类型、个数、顺序 。
  • 参数传递有两种方式 。
    • 传值方式（参数为整型、实型、字符型等）
    • 传地址
      • 参数为指针变量
      • 参为引用类型
      • 参数为数组名

  //传值方式 - 形参的变化不会影响实参a,b的
  #include <iostream.h>
  
  void swap(float m, float n){
      float temp;
      temp = m;
      m = n;
      n = temp;
  }
  
  void main(){
      float a,b;
      cin>>a>>b;
      swap(a,b);
      cout<<a<<endl<<b<<endl;
  }
  
  

//指针变量作参数
// 形参变化影响实参 - 形参所指的具体数发生变化影响了实参
#include <iostream.h>
void swap(float *m, float *n){
    float t;
    t = *m; // 指针所指具体内容发生变化
    *m = *n;
    *n = t;
}

void main(){
    float a,b，*p1,*p2;
    cin>>a>>b;
    p1=&a; p2=&b; // a,b的指针设为p1,p2
    swap(p1,p2);
    cout<<a<<endl<<b<<endl;
}

// 形参变化不影响实参 - 形参中只有指针的变化不会影响实参
#include <iostream.h>
void swap(float *m, float *n){
    float *t;
    t = m; // 指针发生交换而已
    m = n;
    n = t;
}

void main(){
    float a,b，*p1,*p2;
    cin>>a>>b;
    p1=&a; p2=&b; // a,b的指针设为p1,p2
    swap(p1,p2);
    cout<<a<<endl<<b<<endl;
}

文章来源地址https://www.toymoban.com/news/detail-436623.html

//引用类型作为参数
#include <iostream.h>

void swap(float &m, float &n){ //形参为引用类型，和实参指向同一块地址，所以会一起变
    float temp;
    temp = m;
    m = n;
    n = temp;
}

void main(){
    float a,b;
    cin>>a>>b;
    swap(a,b);
    cout<<a<<endl<<b<<endl;
}

• 总结： 引用类型作为形参，在内存中不产生副本，直接对实参操作；而一般变量作为参数需要不通的存储单元，当传递数据量较大时会影响空间效率。指针参数能达到同样效果但是阅读性差因为需要重复使用*变量名操作。

TO BE CONTINUED…

到了这里，关于数据结构与算法基础（青岛大学-王卓）(1)的文章就介绍完了。如果您还想了解更多内容，请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章，希望大家以后多多支持TOY模板网！